Основные правила преобразования структурных схем ДСАУ. Примеры типовых преобразований. Различие формирования структурных схем, как расчетных и имитационных моделей, страница 4

³⁾Примечание 3. Очень полные таблицы в специальной книге [55], менее полные, но достоверные таблицы в источниках [6], [9]. Зарубежный (переведенный)источник[1], имеет хорошие таблицы z -преобразований.

Теория вычетов - это важный раздел теории функций комплексной переменной. В этом же разделе математики содержатся основы всех конформных преобразований Лапласа, Фурье, Мёбиуса, " z " и др. Мы (инженеры) постоянно пользуемся этими преобразованиями не только в "Теории управления", но и во всех других науках. Почти половина терминов нашего профессионального общения базируется на этих понятиях. Полезно иметь свое представление об этих основах.

Пример: , где α=Т₁^-1.

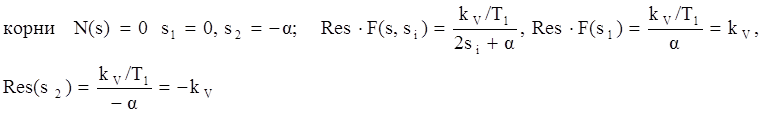
Следовательно:

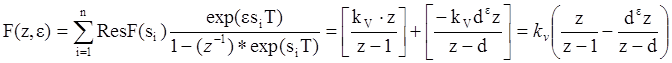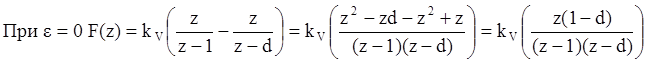Замечание (практически очень важное). Часто пользуются зарубежной переводной литературе, где есть таблицы  преобразований, Однако вместо "российского" понятия "смещенных" функций F(z, ε) в них используется понятие "модифицированных" функций F(z, m). При этом нужно иметь в виду, что формально  m–1=ε. Поэтому: F(z, ε)= z ×F(z, m).

4. 3.Вычисление смещенных и несмещенных дискретных передаточных функций (ДПФ) в ДСАУ с экстраполятором нулевого порядка.

Передаточная функция экстраполятора 0-го порядка была нами ранее представлена в виде К_Э0(s)=(1–e^-sT)/s. Представим, что таким экстраполятором "с запоминанием на полный интервал" (квантования) (γ=1) предваряется некоторый непрерывный объект управления с передаточной функцией К_О(s).

Тогда запишем:

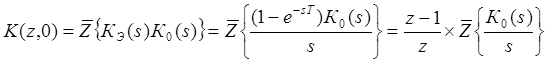.               (8. 6.)

Если необходимо найти смещенное z преобразование той  же комбинации, то получим:

.                                           (9.6.)

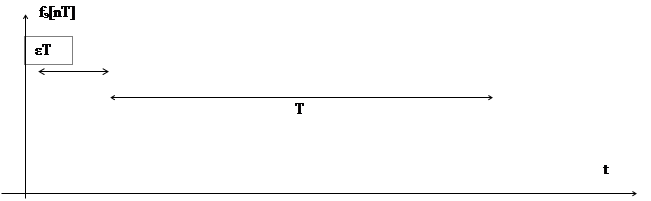
В выражениях (8. 6) и (9. 6.) принято: . Эти преобразования находятся по упомянутым ранее таблицам. Сложнее находятся преобразование той же комбинации блоков, если "интервал запоминания" экстраполятора  (См. рис. 4. 6).

Здесь импульс имеет продолжительность γΤ, а величина интервала εТ может быть и меньше (см. рис. 4. 6) и больше γΤ. Тогда при εТ< γΤ  информацию находят в последующем (правом) интервале, а затем "возвращают " её обратно домножением преобразований на z^-1. Это выглядит так:

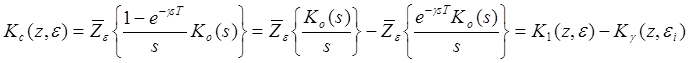.  (10.6.)

 

γΤ                                                                      (γ+1)Τ

Рис. 4.6

Обратим внимание на то, что расчеты по формуле (10.6.) выполняются различным образом.

При εТ < γΤ будем иметь:

,                                                                          (10¹. 6.)

.                                                (10². 6.)

Итак, например, если задано ε= 0,4, а γ =0,6, то (10¹. 6) находится при ε= 0,4, но  определяется при=. Напоминаем, что найденное выражение ,согласно (10². 6.), умножается на z^-1.

При εТ > γΤ преобразования выражения (10. 6) будут иным. Первое слагаемое определяется так же (10¹. 6.) .Но второе слагаемое будет:

.                                                      (10³. 6.)

Последнее выражение существенно отличается от формулы (10². 6.).

Наконец, рассмотрим применение (10. 6) для несмещённых  функций , тогда ε =0 и (10¹. 6.) находится как несмещённое преобразование, а (10².6.)определяется при ε₁=1- γ.

Скорректировано 16.03.09. Повторно скорректировано 25.03.10.