Основные правила преобразования структурных схем ДСАУ. Примеры типовых преобразований. Различие формирования структурных схем, как расчетных и имитационных моделей, страница 3

¹⁾Примечание 1.⁾. Здесь следует оговориться. Обычно для синтеза ДСАУ предлагается использовать метод пространства состояний (МПС) – в том числе и для работы в "z"-плоскости. По убеждению. С Ковчина, все это не просто и не так достоверно.

Дело в том, что, во-первых, для использования МПС необходимо знать корни синтезированной (уже синтезированной!) ДСАУ. Во-вторых, при этом используются стандартные формы полиномов знаменателей замкнутых систем. А по ним еще надо знать и уметь найти структуру синтезированной системы при заданной структуре силовой части ЭМС. При этом выбранная структура модели может плохо подходить под "стандартные формы". В третьих, синтезированная система не должна иметь нулей, – то есть вообще числитель ее передаточной функции должен представляться константой. В другом случае нули должны иметь заданный порядок (не выше второго) и параметры, тогда задается и астатизм разомкнутой системы. Наконец, в четвертых, стандартные формы полиномов есть только для аналоговых систем. Для моделей ДСАУ их нет. Рассмотрим полином  знаменателя замкнутой аналоговой системы:

N(s)=a₀s³+a₁s²+a₂s+a₃.

Пусть корнями N(s) являются вещественные числа s₁, s₂ и s₃.

Тогда: N(s)=a₀(s–s₁)(s–s₂)(s–s₃).

При переходе к z-изображению мы получим следующее выражение: N(z)=b₀z³+b₁z²+b₂z¹+b=b₀(z–z₁)(z–z₂)(z–z₃).Однако ведь в этой формуле корни не являются конкретными числами:z₁=exp(s₁T), z₂=exp(s₂T), z₃=exp(s₃T). Они же зависят от периода квантования!!! Теперь мы имеем дело с множеством комплектов корней. Ввиду этих сложностей, метод пространства состояний в данном курсе рассматриваться не будет. Взамен ему у нас (на кафедре САУ СПбГПУ, бывшего ЛПИ) разработан альтернативный метод Ковчина-Шендеровского-Муафака. Этот метод позволяет синтезировать системы в плоскости Z, во временной области.

4.2. Вычисление  - преобразования РФ с помощью вычетов²⁾

Для  - преобразований смещенных и несмещенных решетчатых функций, естественно, имеются специальные таблицы³⁾. Процедура получения -преобразований основана на использовании вычетов аналитической функции F(s) в особых точках (полюсах) s_i.

Покажем процедуру вычисления z-преобразований в этих таблицах для функций полином N(s) имеет только простые корни. Тогда формула для смещенных z-преобразований будет такой:

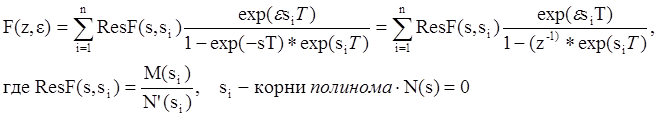. (6.6.)

Формулу для несмещенного z-преобразования получим из выражения (6. 6.) при ε=0:

. (7.6)

В случае кратных корней следует применять более сложную формулу. Впрочем, такие случаи, разумеется, встречаются нечасто.

Продемонстрируем использование указанного метода.

_____________________________________________________________________________

Примечание 2 (Р.Горковенко). Учебные группы приема 2003 г. очень "удачно" попали на период организационного "эксперимента", связанного с уменьшением времени академической "пары" до 1 часа 15 минут. В связи с этим, а также с тем, что курс математики был лишь в течение 3 семестров, чтение материала по вычетам прошло в достаточно сжатой форме. Поэтому, на мой взгляд, актуально рассмотреть эту тему "с бóльшим пристрастием". (С.Ковчин) Согласен, что сокращение (по любым причинам) установившегося курса математики при дальнейшем обучении где - то " аукнется не по доброму". Обещаю учесть это в практических занятиях. В лекциях же я хотел только пояснить процедуру (методику получения) -преобразований