|
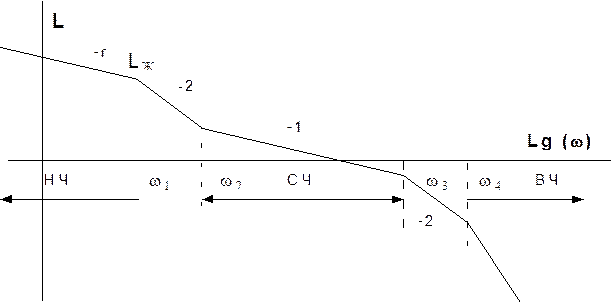
Рис. 8. Вид типовой желаемой логарифмической частотной характеристики. |
Желаемая ЛАХ формируется на основе технических требований к точности (низкочастотная область (НЧ) и динамическим характеристикам (среднечастотная область (СЧ) ЛАХ проектируемой системы.
3.1. Логарифмическая амплитудно-частотная характеристика нескорректированной разомкнутой системы
Асимптотические логарифмические частотные характеристики исходной системы имеют вид рис.9 для системы стабилизации (r=0) и рис.10 для следящей системы (r=1)..
ЛАХ исходной системы (рис. 9, 10) показаны для
соотношения постоянных времени ТМ/ТЭ<4. В случае,
если это соотношение будет больше 4 следует заменить выражение ![]() на
на ![]() в
передаточных фукнциях, а Lисх(ω)
будут иметь наклоны не 0 - 1 - 2-…,
а 0 - 2… для статической системы (рис. 9), и не 1 - 2 - 3 -…, а 1 - 3 - …
для астатической системы (рис. 10).
в
передаточных фукнциях, а Lисх(ω)
будут иметь наклоны не 0 - 1 - 2-…,
а 0 - 2… для статической системы (рис. 9), и не 1 - 2 - 3 -…, а 1 - 3 - …
для астатической системы (рис. 10).
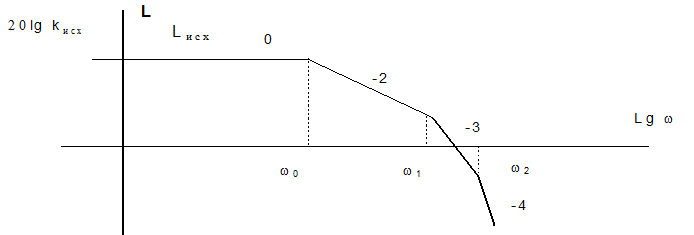
Рис. 9. ЛАХ исходной системы
стабилизации ![]() .
.
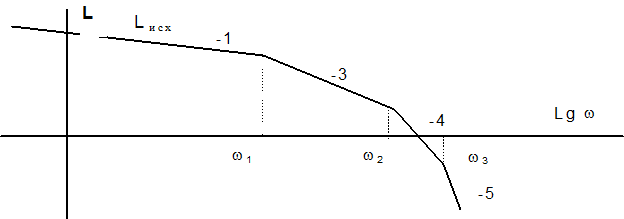
Рис.
10. ЛАХ исходной следящей системы ![]() .
.
3.2. Построение " запретной зоны по точности" для "желаемой" логарифмической амплитудно-частотной характеристики скорректированной системы по заданным динамическим и статическим параметрам механизма
Конфигурация запретной зоны в низкочастотной области
определяется характером изменения входного сигнала во времени и требованиями к
точности его воспроизведения. Первоначально необходимо вычислить значения ![]() ,
, ![]() и
и
![]() по заданным kv, kа, и емакс (см п.1.2.2.).Согласно
техническому заданию (табл.1) в курсовой работе студентом рассматривается один
из двух вариантов.
по заданным kv, kа, и емакс (см п.1.2.2.).Согласно
техническому заданию (табл.1) в курсовой работе студентом рассматривается один
из двух вариантов.
Входное воздействие g(t)
меняется во времени по произвольному закону, но при ограниченных амплитуды (![]() ), скорости (
), скорости (![]() ) и ускорения (
) и ускорения (![]() ). Кроме того на систему неблагоприятным образом
действуют два возмущения: нестабильность питания сети
). Кроме того на систему неблагоприятным образом
действуют два возмущения: нестабильность питания сети ![]() и момента нагрузки
и момента нагрузки ![]() .
Этому случаю соответствует запретная зона LНЧ (рис.11).
.
Этому случаю соответствует запретная зона LНЧ (рис.11).
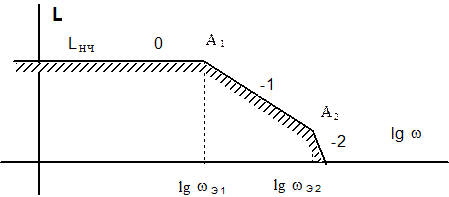
Рис. 11. Запретная зона по точности для системы стабилизации
Координаты точки А1
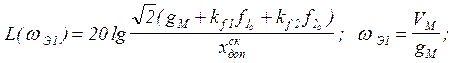 (3.1)
(3.1)
где![]()
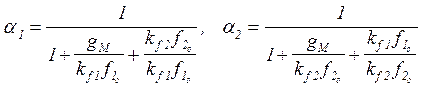 ,
,
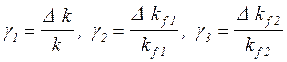
![]() Значения
Значения ![]() приведены в техническом задании (табл.1,2)
и в табл.3.
приведены в техническом задании (табл.1,2)
и в табл.3. ![]() -скорректированное значение
допустимой ошибки, коэффициент Ö2 в формуле (1) применяется,
если
-скорректированное значение
допустимой ошибки, коэффициент Ö2 в формуле (1) применяется,
если ![]() равна или близка к какой-либо из
частот излома ЛАХ исходной системы. В противном случае вместо Ö2 в формуле (3.1) следует подставить 1.0 .
равна или близка к какой-либо из
частот излома ЛАХ исходной системы. В противном случае вместо Ö2 в формуле (3.1) следует подставить 1.0 .
Координата ![]() определяется из выражения
определяется из выражения ![]() .
.
В
случае, когда ускорение ![]() не ограничено,
участок с наклоном -20 дБ/дек на рис.11 продлевается до оси lgw.
не ограничено,
участок с наклоном -20 дБ/дек на рис.11 продлевается до оси lgw.
Запретная зона для этого случая показана на рис.12.
Координата контрольной точки Ак определяется по формулам
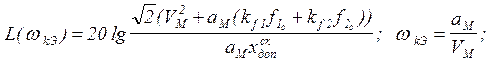 (3.2)
(3.2)
|
Рис. 22 Запретная зона по точности для следящей системы (r=1). |
где![]() ,
, ![]() -
значение допустимой ошибки отработки заданного сигнала,
-
значение допустимой ошибки отработки заданного сигнала, ![]() - значение допустимой ошибки, скорректированное
с учетом нестабильности параметров.
- значение допустимой ошибки, скорректированное
с учетом нестабильности параметров. ![]() - ²уходы² коэффициентов передачи
- ²уходы² коэффициентов передачи ![]() .
Формулы для определения
.
Формулы для определения ![]() приведены в
табл.3. a1 , a2 - доли
составляющей ошибки вследствие действия возмущений f1(t) и f2(t) в
общей ошибке. Эти коэффициенты определяются по формулам:
приведены в
табл.3. a1 , a2 - доли
составляющей ошибки вследствие действия возмущений f1(t) и f2(t) в
общей ошибке. Эти коэффициенты определяются по формулам: 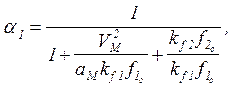
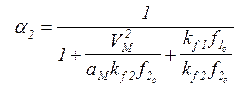 .
Коэффициент Ö2 в формуле (3.2) применяется, если
.
Коэффициент Ö2 в формуле (3.2) применяется, если ![]() равна или близка к какой-либо из
частот излома ЛАХ исходной системы. В противном случае вместо Ö2 в формуле (2) следует подставить 1.0.
равна или близка к какой-либо из
частот излома ЛАХ исходной системы. В противном случае вместо Ö2 в формуле (2) следует подставить 1.0.
3.3. Построение " разрешенной зоны " для "желаемой" логарифмической амплитудно-частотной характеристики скорректированной системы по предельным динамическим параметрам двигателя
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.