Потребности новых районов застройки города в телефонах. Экономико-математическая модель задачи, составленная с помощью модифицированного метода линейного программирования

Министерство Российской Федерации по связи и         информатизации

Сибирский Государственный Университет Телекоммуникаций и Информатики

Межрегиональный центр переподготовки специалистов

Контрольная работа

по дисциплине: «Экономико-математические методы и модели в отрасли связи »

Выполнил слушатель:

                                                                      Группа: ЭДТ – 32

Проверил преподаватель:

г. Тайшет  2006 год

Задача №1

На территории города имеется три телефонные станции А, Б, и В. незадействованные ёмкости станций составляют на станции А-Qа, Б-Qб, В-Qв номеров. Потребности новых районов застройки города в телефонах составляют: 1-Q1, 2-Q2, 3-Q3, 4-Q4 номеров.

Необходимо составить экономико-математическую модель задачи с помощью модифицированного метода линейного программирования найти вариант распределения ёмкостей телефонных станций между районами новой застройки, который обеспечивал бы минимальные затраты как на строительство, так и на эксплуатацию линейных сооружений телефонной сети. Естественно, что таким вариантом при прочих равных условия будет такое распределение ёмкости, при котором общая протяжённость абонентских линий будет минимальной.

Запишем условия задачи в виде таблице:

Станции	Районы				Возмож-ность
	1	2	3	4
А	4	5	6	4	500
Б	3	2	1	4	1100
В	6	7	5	2	900
Спрос	200	500	900	200

Пусть х₁₁, х₁₂, х₁₃, х₁₄,-число номеров со станции А, размещенных соответственно в 1,2,3 и 4-х районах.

Пусть х₂₁, х₂₂, х₂₃, х₂₄,- число номеров со станции Б, размещенных соответственно в 1,2,3 и 4-х районах.

Пусть х₃₁, х₃₂, х₃₃, х₃₄,- число номеров со станции В, размещенных соответственно в 1,2,3 и 4-х районах.

В этом случае целевая функция будет иметь следующий вид:

при ограничениях:

х₁₁+х₁₂+х₁₃+х₁₄500

х₂₁+х₂₂+х₂₃+х₂₄1100

х₃₁+х₃₂+х₃₃+х₃₄900

х₁₁+х₂₁+х₃₁200

х₁₂+х₂₂+х₃₂500

х₁₃+х₂₃+х₃₃900

х₁₄+х₂₄+х₃₄200

х_ij, i=, j=

Сформулированная таким образом задача является задачей линейного программирования  и для ее решения целесообразно воспользоваться симплекс-методом.

Приведем задачу к каноническому виду, для чего введем дополнительные переменные у₁, у₂, у₃, у₄, у₅, у₆, у₇

Получаем:

Ограничения имеют вид:

х₁₁+х₁₂+х₁₃+х₁₄+ у₁=500

х₂₁+х₂₂+х₂₃+х₂₄+ у₂=1100

х₃₁+х₃₂+х₃₃+х₃₄+ у₃= 900

х₁₁+х₂₁+х₃₁+ у₄= 200

х₁₂+х₂₂+х₃₂+ у₅= 500

х₁₃+х₂₃+х₃₃+ у₆= 900

х₁₄+х₂₄+х₃₄+ у₇= 200

Дополнительные переменные вводятся также в целевую функцию с нулевыми коэффициентами.

Видно, что эту задачу можно решить методом линейного программирования, так как число переменных n=19>m=7 (m-число уравнений в ограничениях)

Для решения поставленной задачи необходимо выбрать исходный опорный базис, которому соответствует исходный опорный базис, которому соответствует исходный опорный план. В качестве исходного базиса должна быть выбрана система линейно-независимых векторов из системы ограничений. В частности, для рассматриваемого случая в качестве исходного опорного базиса можно взять исходный опорный план из у₁, у₂, у₃, у₄, у₅, у₆, у₇ не равных нулю и значение целевой функции

Приступим к построению симплекс таблицы: таблица №1, таблица №2, таблица №3, таблица №4, таблица №5, таблица №6, таблица №7.

Таблица 1
Базис	X11	x12	x13	x14	x21	x22	x23	x24	x31	x32	x33	x34	у1	у2	у3	у4	у5	у6	у7	B
Z	4	5	6	4	3	2	1	4	6	7	5	2	0	0	0	0	0	0	0
у1	1	1	1	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	500
у2	0	0	0	0	1	1	1	1	0	0	0	0	0	1	0	0	0	0	0	1100
у3	0	0	0	0	0	0	0	0	1	1	1	1	0	0	1	0	0	0	0	900	900
у4	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	0	200
у5	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	500	500
у6	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	900
у7	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	200
Ведущий столбец х32, ведущая строка у5
Таблица 2
Базис	X11	x12	x13	x14	x21	x22	x23	x24	x31	x32	x33	x34	у1	у2	у3	у4	у5	у6	у7	B
Z	4	-2	6	4	3	-5	1	4	6	0	5	2	0	0	0	0	-7	0	0
у1	1	1	1	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	500
у2	0	0	0	0	1	1	1	1	0	0	0	0	0	1	0	0	0	0	0	1100
у3	0	-1	0	0	0	-1	0	0	1	0	1	1	0	0	1	0	-1	0	0	400	400
у4	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	0	200	200
х32	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	500
у6	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	900
у7	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	200
Ведущий столбец х31, ведущая строка у4
Таблица 3
Базис	X11	x12	x13	x14	x21	x22	x23	x24	x31	x32	x33	x34	у1	у2	у3	у4	у5	у6	у7	B
Z	-2	-2	6	4	-3	-5	1	4	0	0	5	2	0	0	0	-6	-7	0	0
у1	1	1	1	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	500	500
у2	0	0	0	0	1	1	1	1	0	0	0	0	0	1	0	0	0	0	0	1100
у3	-1	-1	0	0	-1	-1	0	0	0	0	1	1	0	0	1	-1	-1	0	0	200
х31	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	0	200
х32	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	500
у6	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	900	900
у7	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	200
Ведущий столбец х13, ведущая строка у1
Таблица 4
Базис	X11	x12	x13	x14	x21	x22	x23	x24	x31	x32	x33	x34	у1	у2	у3	у4	у5	у6	у7	B
Z	-8	-8	0	-2	-3	-5	1	4	0	0	5	2	-6	0	0	-6	-7	0	0
х13	1	1	1	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	500
у2	0	0	0	0	1	1	1	1	0	0	0	0	0	1	0	0	0	0	0	1100
у3	-1	-1	0	0	-1	-1	0	0	0	0	1	1	0	0	1	-1	-1	0	0	200	200
х31	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	0	200
х32	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	500
у6	-1	-1	0	-1	0	0	1	0	0	0	1	0	-1	0	0	0	0	1	0	400	400
у7	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	200
Ведущий столбец х33, ведущая строка у3
Таблица 5
Базис	X11	x12	x13	x14	x21	x22	x23	x24	x31	x32	x33	x34	у1	у2	у3	у4	у5	у6	у7	B
Z	-3	-3	0	-2	2	0	1	4	0	0	0	-3	-6	0	-5	-1	-2	0	0
х13	1	1	1	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	500
у2	0	0	0	0	1	1	1	1	0	0	0	0	0	1	0	0	0	0	0	1100	1100
х33	-1	-1	0	0	-1	-1	0	0	0	0	1	1	0	0	1	-1	-1	0	0	200
х31	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	0	200
х32	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	500
у6	0	0	0	-1	1	1	1	0	0	0	0	-1	-1	0	-1	1	1	1	0	200
у7	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	200	200
Ведущий столбец х24, ведущая строка у7
Таблица 6
Базис	X11	x12	x13	x14	x21	x22	x23	x24	x31	x32	x33	x34	у1	у2	у3	у4	у5	у6	у7	B
Z	-3	-3	0	-6	2	0	1	0	0	0	0	-7	-6	0	-5	-1	-2	0	-4
х13	1	1	1	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	500
у2	0	0	0	-1	1	1	1	0	0	0	0	-1	0	1	0	0	0	0	-1	900	900
х33	-1	-1	0	0	-1	-1	0	0	0	0	1	1	0	0	1	-1	-1	0	0	200
х31	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	0	200	200
х32	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	500
у6	0	0	0	-1	1	1	1	0	0	0	0	-1	-1	0	-1	1	1	1	0	200	200
х24	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	200
Ведущий столбец х21, ведущая строка у6
Таблица 7
Базис	X11	x12	x13	x14	x21	x22	x23	x24	x31	x32	x33	x34	у1	у2	у3	у4	у5	у6	у7	B
Z	-3	-3	0	-4	0	-1	-1	0	0	0	0	-5	-4	0	-3	-3	-4	-2	-4
х13	1	1	1	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	500
у2	0	0	0	0	1	0	0	0	0	0	0	0	1	1	1	-1	-1	-1	-1	700
х33	-1	-1	0	-1	-1	0	1	0	0	0	1	0	-1	0	0	0	0	1	0	400
х31	1	0	0	1	1	-1	-1	0	1	0	0	1	1	0	1	0	-1	-1	-1	0
х32	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	500
х21	0	0	0	-1	1	1	1	0	0	0	0	-1	-1	0	-1	1	1	1	0	200
х24	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	1	200

Ответ: х₁₃=500, х₂₁=200, х₂₄=200, х₃₁=0, х₃₂=500, х₃₃=400, у₇= 0

х₁₁=х₁₂=х₁₄=х₂₂=х₂₃=х₃₄=у₁=у₃= у₄= у₅=у₆=у₇=0

Примечание: у₂=700-возможность станции Б незадействованная.

Задача №2

Необходимо оценить работу автоматической телефонной станции (АТС), которая имеет n линий связи. Моменты поступления вызовов на станцию являются случайными и независимыми друг от друга. Средняя плотность потока равна λ вызовов в единицу времени. Продолжительность каждого разговора является величиной случайной и подчинена показательному закону распределения. Среднее время одного разговора равно t_обс единиц времени.

Дано:

Количество линий n, n=7

Средняя плотность потока  (вызова в ед.вр)

Среднее время разговора , t_обс=2 (един., времени)

Необходимо оценить работу АТС

Решение:

Определим интенсивность потока обслуживания  обслуживание в ед. времени.

Определим интенсивность нагрузки канала Р

Р= (вызовов)

Таким образом находим вероятности

Р₀-вероятность того, что все каналы свободны

Р₁- вероятность того, что один канал занят, остальные свободные

……

Р₇-вероятность того что все каналы заняты

Р₇=Р_отк (вероятность отказа)

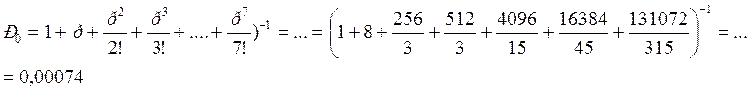
Р_отк=0,3082 (все каналы заняты)

Относительная пропускная способность Q

Абсолютная пропускная способность А

Результаты сведем в Таблицу №1

таблица №1
характеристика обслуживания	Число линий
	1	2	3	4	5	6	7
вероятность (Р)	0,0059	0,0237	0,0632	0,1264	0,2022	0,2696	0,3082
Относительная пропуск.,спо-ть	0,9941	0,9763	0,9368	0,8736	0,7978	0,7304	0,6918
Абсолютная пропуск.,спо-ть	3,9764	3,9052	3,7472	3,4944	3,1912	2,9216	2,7672
р=	8
Ро	0,0007

Ответ:

1)  То есть вероятность того, что будет занят 1 канал, все остальные