Министерство Российской Федерации по связи и информатизации
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
"Экономико-математические методы и модели в отрасли связи"
Контрольная работа
В-10
Выполнила: Макарова Г.Ш.
ЭДВ-55
Проверил:
2006
ЗАДАЧА 1.
На территории города имеется три телефонные станции А, Б, и В. незадействованные ёмкости станций составляют на станции А-Qа, Б-Qб, В-Qв номеров (таблица 1.1). Потребности новых районов застройки города в телефонах составляют: 1-q1, 2-q2, 3-q3, 4-q4 номеров таблицы (таблица 1.2).
Необходимо составить экономико-математическую модель задачи с помощью модифицированного метода линейного программирования найти вариант распределения ёмкостей телефонных станций между районами новой застройки, который обеспечивал бы минимальные затраты как на строительство, так и на эксплуатацию линейных сооружений телефонной сети. Естественно, что таким вариантом при прочих равных условия будет такое распределение ёмкости, при котором общая протяжённость абонентских линий будет минимальной.
Исходные данные:
Таблица 1.1-незадействованные ёмкости телефонных станций.
|
Возможности станций, номеров |
Варианты |
|
10 |
|
|
QА |
600 |
|
QБ |
400 |
|
QВ |
200 |
Таблица 1.2- Спрос на установку телефонов.
|
Спрос районов, номеров |
Варианты |
|
10 |
|
|
Q1 |
200 |
|
Q2 |
160 |
|
Q3 |
240 |
|
Q4 |
600 |
Таблица 1.3-Среднее расстояние от станции до районов застройки, км (для всех вариантов)
|
Станции |
РАЙОНЫ |
|||
|
1 |
2 |
3 |
4 |
|
|
А |
4 |
5 |
6 |
4 |
|
Б |
3 |
2 |
1 |
4 |
|
В |
6 |
7 |
5 |
2 |
Так как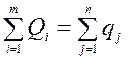 ,1200=1200, у задачи закрытая
транспортная модель. Для решения задачи используется матрица распределительного
метода.
,1200=1200, у задачи закрытая
транспортная модель. Для решения задачи используется матрица распределительного
метода.
Экономико-математическая модель (ЭММ).
Если Xij-количество абонентов j- микрорайона подключаемых к i-ой станции, то модель может быть представлена следующими уравнениями:
xA1+ xA2+ xA3 =600
xБ1+ xБ2+ xБ3 =400
xВ1+ xВ2+ xВ3 =200 выражает ограничение по возможности поставщика (АТС)
Xij![]() 0
0
xA1+ xБ1+ xВ1 =200
xA2+ xБ2+ xВ2+ =160
xA3+ xБ3+ xВ3 = 240
xA4+ xБ4+ xВ4 =600
выражает ограничение по возможности потребителя (АТС)
Для получения исходного допустимого решения используем метод “северо-западного угла”.
В маленьких квадратах указаны расстояния от АТС до районов новой застройки.
В остальной части каждой клетки проставлена величина потребности, удовлетворяемая за счет соответствующей АТС. Для успешного применения распределительного метода количество заполненных клеток должно быть равно m+n-1,где m –количество АТС, а n-количество новых районов. И для нашего примера 4+3-1=6 .Суммы чисел, расположенных в клетках каждой строки, равны возможностям соответствующих АТС, а сумма чисел каждого столбца – потребностям районов.
Таблица 1.4
|
АТС |
Микрорайоны |
Qi |
|||||||||
|
1 |
2 |
3 |
4 |
||||||||
|
А |
4 |
160 |
5 |
6 |
240 |
4 |
600 |
||||
|
200 |
|||||||||||
|
Б |
3 |
2 |
240 |
1 |
160 |
4 |
400 |
||||
|
В |
6 |
7 |
5 |
2 |
200 |
||||||
|
200 |
|||||||||||
|
qj |
240 |
1200 |
|||||||||
|
200 |
160 |
600 |
|||||||||
Проверку полученного плана на оптимальность производим с помощью характеристик ПТЗ (прирост транспортных затрат) для всех свободных мест плана, а находим их с помощью контуров.
Контуры строятся из горизонтальных и вертикальных отрезков прямых по правилу: одна вершина контура должна находиться в свободной клетке, для которой считается характеристика, а все остальные вершины контура должны находиться в занятых местах. У вершины контура проставляются знаки: у вершины, находящейся в свободной клетке ставится всегда "+", а знаки других вершин чередуются "-" , "+" и т.д.
Характеристика свободных мест:
А1=6-1+4-4=5
Б1=3-4+4-4=7
Б2=2-5+4-4=-3
В1=6-4+4-2=4
В2=7-5+4-2=4
В3=5-1+4-2=6
Для определения протяженности линий при распределении емкости АТС умножим требуемую емкость на расстояние от АТС до района застройки
Z1 =200*4+160*5+240*4+240*1+160*4+200*2=3840 км
Так как прирост протяженности для клетки Б2 является отрицательным, то необходима дальнейшая оптимизация распределения емкости между
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.