
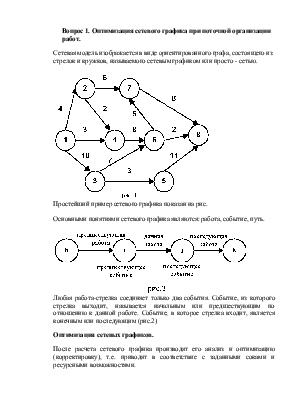






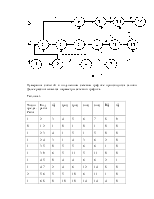











каждой работе создается одна специализированная бригада, которая будет работать на участках в строго определенной последовательности.
Последовательность выполнения любого специализированного потока по участкам рекомендуется принять в порядке возрастания ранних окончаний работ, т. е. сначала на 1, затем на П и наконец, на Ш участке.
Новый сетевой график строится с одноименным добавлением организационных связей, показывающих переход специализированных бригад с одного участка на другой.
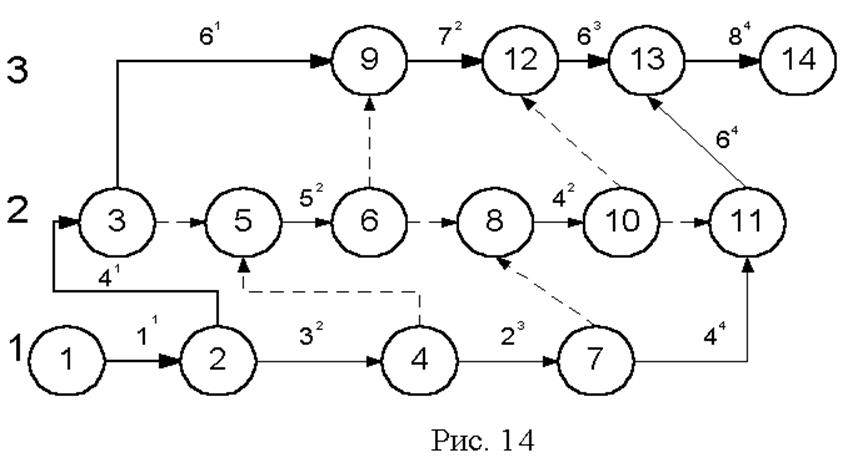
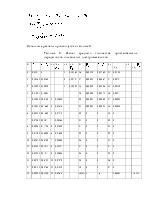
Нумерация событий в полученном сетевом графике производится заново. Далее рассчитываются параметры сетевого графика.
Таблица 4
|
Число предш. Работ |
Код работ |
tij |
tрнij |
tроij |
tпнij |
tпоij |
Rij |
rij |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
1-2 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
2-3 |
4 |
1 |
5 |
1 |
5 |
0 |
0 |
|
1 |
2-4 |
3 |
1 |
4 |
3 |
6 |
2 |
0 |
|
1 |
3-5 |
0 |
5 |
5 |
6 |
6 |
1 |
0 |
|
1 |
3-9 |
6 |
5 |
11 |
5 |
11 |
0 |
0 |
|
1 |
4-5 |
0 |
4 |
4 |
6 |
6 |
2 |
1 |
|
1 |
4-7 |
2 |
4 |
6 |
12 |
14 |
8 |
0 |
|
2 |
5-6 |
5 |
5 |
10 |
6 |
11 |
1 |
0 |
|
1 |
6-8 |
0 |
10 |
10 |
14 |
14 |
4 |
0 |
|
1 |
6-9 |
0 |
10 |
10 |
11 |
11 |
1 |
1 |
|
1 |
7-8 |
0 |
6 |
6 |
14 |
14 |
8 |
4 |
|
1 |
7-12 |
4 |
6 |
10 |
14 |
18 |
8 |
4 |
|
2 |
8-10 |
4 |
10 |
14 |
14 |
18 |
4 |
0 |
|
2 |
9-12 |
7 |
11 |
18 |
11 |
18 |
0 |
0 |
|
1 |
10-11 |
0 |
14 |
14 |
18 |
18 |
4 |
0 |
|
1 |
10-12 |
0 |
14 |
14 |
18 |
18 |
4 |
4 |
|
2 |
11-13 |
6 |
14 |
20 |
18 |
24 |
4 |
4 |
|
2 |
12-13 |
6 |
18 |
24 |
18 |
24 |
0 |
0 |
|
2 |
13-14 |
8 |
24 |
32 |
24 |
32 |
0 |
0 |
Новый критический путь равен 32 дням и проходит по всем трем участкам : вначале по 1, потом по П и затем по Ш.
Вопрос 2. Расчет оптимальной нормы обслуживания технических устройств методами теории массового обслуживания
Для разработки оптимальных норм обслуживания необходимо рассчитать показатели обслуживания для конкретных условий при различном числе обслуживаемого персонала.
Рассмотрим определение норм обслуживания на примере.
Требуется установить норму численности дежурных электромехаников, обслуживающих приёмные и вещательные передатчики.
В цехе установлено 30 передатчиков. В результате исследований процесса методом фотографии рабочего дня получены следующие данные: среднее количество требований на обслуживание, поступающих в одну минуту от каждого передатчика, равно 0,0078, среднее время обслуживания одного передатчика - 12,48 мин., средняя продолжительность времени между двумя последовательными требованиями (время спокойной работы) - 121,4 мин.
Проанализируем входящий поток и распределение времени обслуживания.
Входящим потоком в данном примере является поток требований на обслуживание передатчиков, которое заключается в устранении причин выхода из строя, настройки и т.п.
Если поток
простейший, то интервал времени между двумя последовательными требованиями
подчиняется показательному закону распределения с параметром λ. При этом
среднее время спокойной работы обратно пропорционально параметру λ, т.е. 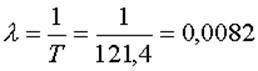 ,
что весьма близко к результату полученному путём фотографии рабочего дня
(0,0078). Это служит ещё одним подтверждением того, что рассматриваемый поток
является простейшим. Для дальнейших расчётов принимает:
,
что весьма близко к результату полученному путём фотографии рабочего дня
(0,0078). Это служит ещё одним подтверждением того, что рассматриваемый поток
является простейшим. Для дальнейших расчётов принимает:
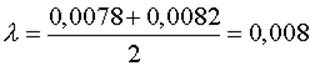
Проверка соответствия эмпирического распределения времени обслуживания теоретическому показывает, что время обслуживания также подчиняется показательному закону распределения. Следовательно:
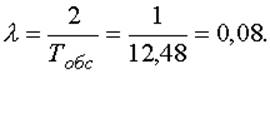
Таким образом, необходимо рассчитать характеристики системы массового обслуживания при простейшем потоке требований с показательным законом распределения времени обслуживания. В этом случае вероятность того, что в системе обслуживания с n - передатчиками обслуживания электромеханиками в момент времени t находится k требований определяется по формулам (13) и (14).
Значение ![]() определяется
из равентства
определяется
из равентства
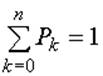
Характеристики системы рассчитываются по формулам с (15) по (22).
Для установления нормы численности дежурных электромехаников вначале рассчитываются параметры системы при условии, что обслуживание всего оборудования осуществляет 3 электромеханика.
Прежде всего,
определяется ![]()
Вероятности ![]() ,
,
![]() и
(k≤r, где z=3) определяются по формулам (13)
и
(k≤r, где z=3) определяются по формулам (13)
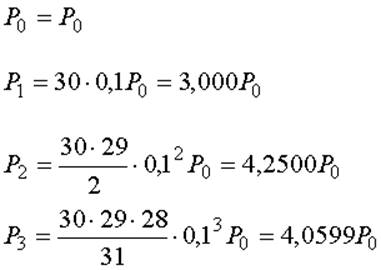
Вероятности ![]() определяются
по формулам (14).
определяются
по формулам (14).
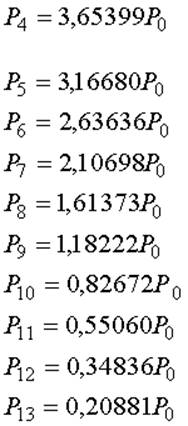
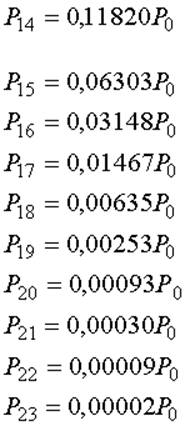
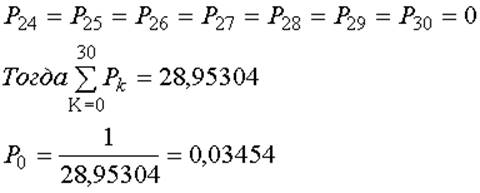
Остальные расчёты производятся в таблице 6.
Таблица 6. Расчёт среднего количества простаивающих передатчиков и незанятых электромехаников
|
K |
|
|
k-r |
(k-r) |
r-k |
(r-k) |
K |
|
|
k-r |
(k-r) |
r-k |
(r-k) |
|
0 |
0,0354 |
0 |
3 |
0,10362 |
16 |
0,00110 |
0,01760 |
13 |
0,01430 |
- |
- |
||
|
1 |
0,10362 |
0,10362 |
2 |
0,20724 |
17 |
0,00051 |
0,00867 |
14 |
0,00714 |
- |
- |
||
|
2 |
0,15025 |
0,30050 |
1 |
0,15025 |
18 |
0,00022 |
0,00396 |
15 |
0,00330 |
- |
- |
||
|
3 |
0,14023 |
0,42063 |
- |
- |
19 |
0,00009 |
0,00171 |
16 |
0,00144 |
- |
- |
||
|
4 |
0,12620 |
0,50480 |
1 |
0,12620 |
- |
- |
20 |
0,00003 |
0,00060 |
17 |
0,00051 |
- |
- |
|
5 |
0,10938 |
0,54690 |
2 |
0,21876 |
- |
- |
21 |
0,00001 |
0,00021 |
18 |
0,00018 |
- |
- |
|
6 |
0,09115 |
0,54690 |
3 |
0,27345 |
- |
- |
22 |
0 |
0 |
19 |
0 |
- |
- |
|
7 |
0,07292 |
0,51044 |
4 |
0,29168 |
- |
- |
23 |
0 |
0 |
20 |
0 |
- |
- |
|
8 |
0,05591 |
0,44728 |
5 |
0,27955 |
- |
- |
24 |
0 |
0 |
21 |
0 |
- |
- |
|
9 |
0,04100 |
0,36900 |
6 |
0,24600 |
- |
- |
25 |
0 |
0 |
22 |
0 |
- |
- |
|
10 |
0,02870 |
0,28700 |
7 |
0,20090 |
- |
- |
26 |
0 |
0 |
23 |
0 |
- |
- |
|
11 |
0,01913 |
0,21043 |
8 |
0,15304 |
- |
- |
27 |
0 |
0 |
24 |
0 |
- |
- |
|
12 |
0,01212 |
0,14544 |
9 |
0,10908 |
- |
- |
28 |
0 |
0 |
25 |
0 |
- |
- |
|
13 |
0,00727 |
0,09451 |
10 |
0,07270 |
- |
- |
29 |
0 |
0 |
26 |
0 |
- |
- |
|
14 |
0,00412 |
0,05768 |
11 |
0,04532 |
- |
- |
30 |
0 |
0 |
27 |
0 |
- |
- |
|
15 |
0,00220 |
0,03300 |
12 |
0,02640 |
- |
- |
итого |
1 |
4,6 |
2,06093 |
0,46111 |
На основании
данных таблицы 6 определяем коэффициент простоя одного передатчика 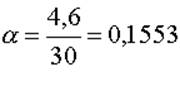 ,
коэффициент простоя передатчика в ожидании обслуживания
,
коэффициент простоя передатчика в ожидании обслуживания 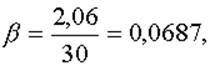 коэффициент
простоя дежурных электромехаников
коэффициент
простоя дежурных электромехаников 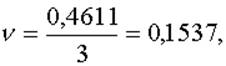 .
Следовательно, при обслуживании 30 передатчиков тремя дежурными
электромеханиками простои передатчиков (на обслуживании и в ожидании
обслуживания) составляют 15,33% времени работы, а постои электромехаников
(из-за отсутствия отказов) - 15,37% рабочего времени.
.
Следовательно, при обслуживании 30 передатчиков тремя дежурными
электромеханиками простои передатчиков (на обслуживании и в ожидании
обслуживания) составляют 15,33% времени работы, а постои электромехаников
(из-за отсутствия отказов) - 15,37% рабочего времени.
Для разработки оптимальных норм обслуживания необходимо рассчитывать показатели обслуживания на различном числе дежурных электромехаников (например, при работе 4,5,6 и т.д. электромехаников).
Результаты расчёта аналогичные таблице 6 приведены в таблице 7.
Таблица 7
|
Показатели системы обслуживания |
Число дежурных электромехаников |
|||
|
3 |
4 |
5 |
6 |
|
|
Коэффициент простоя передатчика |
0,1533 |
0,1065 |
0,095 |
0,092 |
|
Коэффициент простоя передатчика в ожидании обслуживания |
0,0687 |
0,0172 |
0,0045 |
0,0011 |
|
Коэффициент простоя электромеханика |
0,1537 |
0,3299 |
0,4557 |
0,5457 |
Данные таблицы 7 могут быть использованы для установления оптимальной по определённому критерию нормы численности дежурных электромехаников. Так если, поставлена цель установить такие нормы численности, при которых общие потери от простоев оборудования и дежурного персонала были бы наименьшими (при стоимости одного часа простоя электромеханика 1 руб., а одного часа простоя одного передатчика 3 руб.). Тогда общие потери за один час работы 30 передатчиков составят:
3 электромеханикам 30∙0,1533∙3+3∙0,1537∙1=14,26 руб/час
4 электромеханикам 30∙0,1065∙3+4∙0,3299∙1=10,90 руб/час
5 электромеханикам 30∙0,095∙3+5∙0,4557∙1=10,83 руб/час
6 электромеханикам 30∙0,092∙3+6∙0,5457∙1=11,55 руб/час
Следовательно, оптимальная норма численности (по критерию минимальных суммарных потерь) составляет 5 дежурных электромехаников на 30 передатчиков.
Следует отметить, что практически санкции за 1 час простоя передатчиков во много крат превосходят потери от простоя единицы дежурного персонала и поэтому при любых условиях снижения коэффициента простоя оборудования для радиопредприятий выгоднее.
Расчёт оптимальных норм обслуживания по графикам.
В качестве критерия экономической эффективности обслуживания
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.