Для определения основных кинематических параметров процесса качения представим колесо в виде плоского обода (рис. 4.2), недеформируемого в радиальном и тангенциальном направлениях. Рассмотрим равномерное качение колеса по недеформируемой поверхности без скольжения и буксования. Тогда мгновенная ось вращения совпадает с точкой О1 на пересечении вертикальной оси и линии опорной поверхности.
Точки, расположенные на ободе колеса, совершают движение двух видов: относительное и переносное. Относительное движение — это вращение колеса вокруг его геометрической оси в точке О со скоростью v0=ωкrк. Переносное движение — это поступательное движение, осуществляемое вместе с осью и трактором со скоростью vп. Абсолютная скорость движения любой точки, расположенной на ободе колеса, может быть найдена сложением векторов этих скоростей. Например, для точки А
(4.6)
Вектор скорости 
в переносном движении направлен в
сторону поступательного движения колеса и параллелен поверхности, по которой
колесо перемещается. Вектор скорости в относительном движении 
направлен в сторону вращения колеса,
касательно к точке обода, т. е. его направление постоянно изменяется по закону
косинуса. На рисунке 4.2 показан графический метод определения абсолютных
скоростей разных точек обода в одно и то же время или одной и той же точки в
разных положениях (в разное время). Результирующая скорость 
точки А во вращательном движении
относительно мгновенного центра О1, направлена в сторону движения колеса
параллельно опорной поверхности и равна сумме векторов +
, а модуль ее равен сумме модулей векторов
(4.6) или
Аналогично результирующая скорость точки В
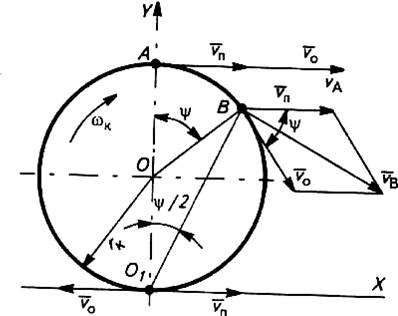
Рисунок 4.2 - Кинематика качения колеса с жестким ободом
Полученный результат
свидетельствует о том, что в точке А скорости относительного и
переносного движений численно равны между собой (ωкrк) и
направлены в одну и ту же сторону. В точке О1 результирующая
скорость 
.
Можно выделить две группы режимов качения колеса, определяемых способом привода колеса во вращение (ведомое, ведущее, тормозящее) и физико-механическими свойствами поверхности качения и колеса. Колесо считается ведомым, если оно катится под действием толкающей силы, приложенной к оси колеса. Колесо приводится во вращение моментом, который образуется толкающей силой и силой трения обода с поверхностью качения на плече, равном радиусу колеса.
Колесо называется ведущим, если оно катится под действием крутящего момента, передаваемого трансмиссией машины от двигателя.
Колесо считается тормозящим, если оно подвержено действию тормозного момента, приложенного к ступице.
В зависимости от конструкции колеса и характера поверхности его качения различаются следующие варианты режимов качения колеса:
• качение колеса с жестким ободом по недеформируемой поверхности. Примером может служить качение железнодорожных колес по рельсам, а в тракторах — опорных катков по гусенице;
• качение колеса с жестким ободом по деформируемой поверхности. К этому варианту можно отнести с некоторым допущением равномерное качение без вертикальных колебаний колеса, с пневматической шиной высокого давления по слабо несущему грунту;
• качение эластичного колеса по недеформируемой поверхности. С некоторым допущением это качение пневматической шины низкого давления по дороге с твердым покрытием;
• качение колеса с эластичным ободом по деформируемой поверхности. Это наиболее типичный случай в эксплуатации сельскохозяйственных тракторов.
4.2.2. Качение пневматического колеса по деформируемой поверхности
Основная проблема, исследуемая в теории качения ведомого колеса — сопротивление качению. Рассмотрим общий случай равномерного качения ведомого колеса мо горизонтальной поверхности: шина эластичная, поверхность качения деформируемая. В этом случае сообщаемая колесу энергия затрачивается на выполнение трех видов работ, составляющих общую энергию сопротивления качению колеса:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.