Поэтому сопротивление качению ведущего колеса следует определять при работе его под разной тяговой нагрузкой. Метод буксировки или протягивания, рекомендуемый для ведомого колеса, не обеспечивает необходимую точность определения коэффициента fк применительно к ведущему колесу.
На рисунке 4.6 показано изменение параметров, характеризующих качение ведущего колеса при разной вертикальной нагрузке. Сила сопротивления качению Pfпрактически линейно растет с увеличением нормальной нагрузки, а касательная сила Рк после достижения GH некоторого значения почти не увеличивается. Результирующая сила Ркр имеет явно выраженный перегиб, отражающий закономерность изменения составляющих Рf и Рк и соответствующий определенному нормальному усилию, равному в рассматриваемом варианте приблизительно 20 кН.
Важно отметить, что максимальное значение КПД ведущего колеса соответствует значениям тяговых сил Рк и Ркр, значительно меньшим максимальных.
Все рассмотренные ранее факторы, так или иначе влияющие на сопротивление качению и буксование ведущего колеса, соответствующим образом отражаются и на коэффициенте полезного действия.
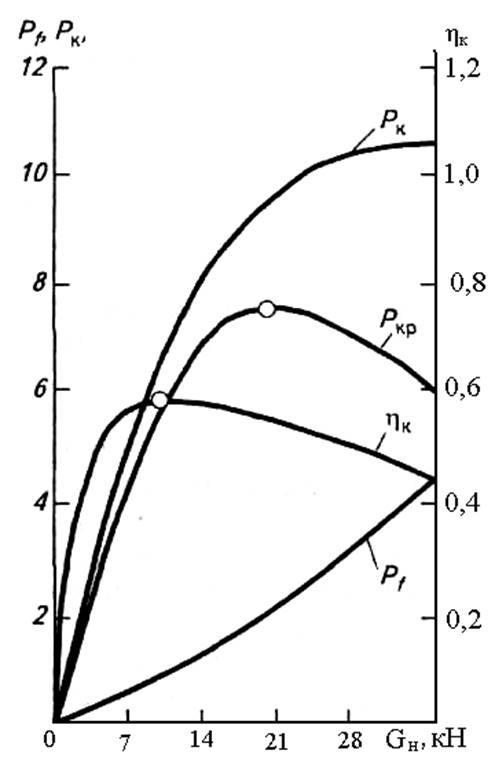
Рисунок 4.6 - Показатели тягово-сцепных свойств колеса
с шиной 12—38 на стерне
4.4. Работа гусеничного движителя
4.4.1. Кинематика гусеничного движителя
Радиус качения. При анализе движения гусеницы относительно поверхности пути предполагается, что шаг звеньев бесконечно мал, гусеница не растягивается и не провисает, а опорная поверхность не деформируется.
При условии равномерного вращения ведущих колес (ωк = const), отсутствии буксования и скольжения гусениц относительно ведущего колеса теоретическая поступательная скорость гусеничного трактора определится по формуле
vT=ωкrк, где ωк - угловая скорость ведущего колеса; rк - радиус ведущего колеса гусеничного движителя.
В действительности гусеница состоит из отдельных звеньев и не является бесконечной гибкой лентой. При всех прочих условиях путь Sn, пройденный трактором за один оборот ведущего колеса, будет равен периметру многоугольника, составленного из звеньев гусеницы, уложенных по всей окружности ведущего колеса (рис. 4.7). Периметр такого многоугольника равен произведению длины одного звена lзв (шага гусеничной цепи) на число зубьев znведущего колеса, принимающих участие в зацеплении за один его оборот
Sn=lзвzn=2πrк.
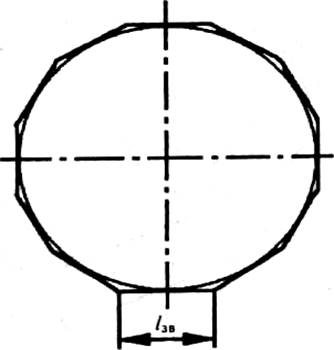
Рисунок 4.7 - Схема укладки звеньев на ведущем колесе
гусеничного движителя
Отсюда радиус ведущего колеса гусеничного движителя
rк=lзвzn/2π. (4.17)
Полученное выражение некорректно для определения кинематического радиуса rк, потому что изначально в качестве радиуса принято расстояние от оси колеса до точки зацепления звена с ведущим колесом, т.e. до точки приложения касательной силы. Основным фактором, определяющим разницу между динамическим и кинематическим радиусами ведущего колеса гусеничного движителя, является его буксование. Отсутствует радиальная деформация ведущего колеса, свойственная эластичной шине, а характер взаимодействия звена гусеничной цепи и ведущего колеса исключает возможность взаимного их проскальзывания. Буксование же гусеничного движителя на сельскохозяйственных фонах не превышает 5 %. При прямолинейном движении с номинальной тяговой нагрузкой буксование чаще всего составляет 2-3 %. Поэтому для практических расчетов можно принять, что кинематический rк и динамический rд радиусы гусеничного движителя равны между собой.
Скорость движения гусеничного трактора. Гусеничная цепь, замкнутая по образованному ведущим колесом, поддерживающими и опорными катками и направляющим колесом контуру составляет гусеничный обвод.
При равномерном вращении ведущего колеса скорость наматывания гусеничного обвода неравномерная. Причиной является звенчатость гусеничной цепи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.