Прямолинейное движение автомобиля. Силы и моменты, действующие на автомобиль при прямолинейном движении, страница 11

P_пp=m_прgψ+δ_вр.прm_пj+P_wпр,                          (2.42)

где m_пр - масса прицепа; δ_вр.пр - коэффициент приведенной массы прицепа; j - ускорение прицепа: j=dv/dt; P_wпр - сила сопротивления воздуха движению прицепа.

Если рассматривать движение автопоезда как единой системы, тогда целесообразно использовать уравнение, аналогичное уравнению (2.41):

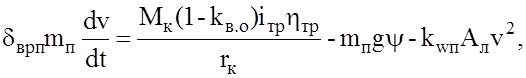  (2.43)

где δ_врп - коэффициент приведенной массы автопоезда (отличается от δ_вр учетом моментов инерции колес прицепа); m_п - масса автопоезда; k_wп - коэффициент сопротивления воздуха: k_wп=(1,2-1,3)k_w.

Если значения моментов инерции J_д, J_тр, J_к.н, J_к.в неизвестны, то δ_вр (или δ_врп) определяют по эмпирической формуле

                 (2.44)

где δ₁=0,03-0,05; δ₂=0,04-0,06; m_a — полная масса автомобиля (автопоезда); m_х — фактическая масса автомобиля.

Для случая движения автомобиля с отсоединенным от трансмиссии двигателем (накат, торможение) δ₂=0. Тогда δ_вр≈1,05.

2.6.2. Движения при буксовании ведущих колес

При движении автомобиля по дороге с низким коэффициентом сцепления и высоким сопротивлением движению (крутой подъем, размокшая грунтовая дорога, движение с прицепом и др.), когда М_в>0,6М_φ, необходимо учитывать внешнее скольжение (буксование) ведущих колес. В этом случае автомобиль при прямолинейном движении необходимо рассматривать как систему с двумя степенями свободы и использовать две независимые фазовые координаты для описания параметров его движения. Выберем в качестве фазовых координат угловую скорость ведущего колеса ω_в и линейную скорость центра масс υ и составим два дифференциальных уравнения.

Первое уравнение получим, рассматривая систему моментов, действующих на ведущее колесо. При неустановившемся движении на ведущее колесо действуют моменты М_в, M_fв, М_jк.в и момент силы сцепления колеса с опорной поверхностью M_φ. Сила сцепления равна предельному значению продольной реакции дороги R_xφ=φ_xR_zв. Момент этой силы относительно оси вращения колеса определяется по формуле M_φ=φ_xR_zвr_д. Динамический радиус колеса r_д примерно равен радиусу качения ведомого колеса r_к, поэтому примем r_д=r_к. В результате

M_φ=φ_xR_zвr_к.                                     (2.45)

Составим общее уравнение динамики ведущего колеса, из которого получим:

М_в-М_fв-М_jв-М_φ=0.                            (2.46)

Инерционный момент ведущих колес М_jк.в

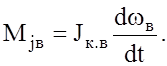                                (2.47)

Для определения подводимого к ведущему колесу момента М_в используем выражение (2.28). Принимая во внимание, что v=r_кω_в, получим:

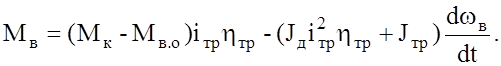      (2.48)

После подстановки значений моментов в выражение (2.46) получим первое дифференциальное уравнение:

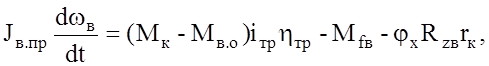       (2.49)

где J_в.пр - приведенный к ведущему колесу суммарный момент инерции двигателя, трансмиссии и колеса:

                    (2.50)

Второе дифференциальное уравнение составляется для поступательного движения корпуса автомобиля. Движущей силой корпуса является тяговая сила ведущего колеса Р_к, приложенная к его оси. При внешнем скольжении эта сила равна силе сцепления ведущего колеса с опорной поверхностью:

                                (2.51)

На корпус действуют силы сопротивления движению Р_i, P_w, P_п. Кроме того, необходимо учесть сопротивление качению ведомых колес и их инерционные моменты. Учитывая эти факторы, получаем второе дифференциальное уравнение:

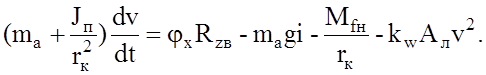       (2.52)

Коэффициент сцепления является функцией двух переменных: φ_х=f(v, ω_в). Поскольку φ_х входит в оба уравнения (2.49) и (2.52), то они представляют собой систему дифференциальных уравнений, решение которых должно осуществляться совместно.