Рассмотрим движение автомобиля без учета внешнего скольжения ведущих колес. Внешнее скольжение практически отсутствует при условии Мв≤(0,4-0,6)Мвφ. Это условие выполняется при движении автомобиля на промежуточных и высших передачах по дороге с твердым покрытием.
При составлении
дифференциального уравнения прямолинейного движения автомобиля используем приведенную
схему системы сил и моментов (рис. 2.1). Составим общее уравнение динамики,
применив принцип Лагранжа - Даламбера, согласно которому алгебраическая сумма работ
всех внешних сил и моментов, приложенных к системе, реакций неидеальных связей
и сил инерции на возможных перемещениях системы равна нулю. Введем следующие
возможные перемещения системы: линейное перемещение центра масс автомобиля 
, угловые перемещения ведомого колеса 
и ведущего 
.
Учитывая взаимные направления сил и моментов и соответствующих им векторов возможных перемещений, получаем общее уравнение динамики:
(2.33)
Установим соотношения между возможными перемещениями δφ1, δφ2 и δх при условии отсутствия внешнего скольжения колес:
(2.34)
(2.35)
Подставим в уравнение (2.33) значения Мв из формулы (2.32) и Рi из формулы (2.2). Используем также выражения (2.34), (2.35), и выражения для определения силы инерции Рjп и инерционных моментов Мjк1, Мjк2. В результате получим:
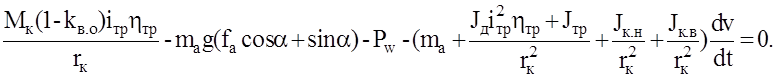
где Jк.н, Jк.в - суммарные моменты инерции соответственно всех ведомых и ведущих колес.
Объединим все члены этого выражения, содержащие ускорение автомобиля dv/dt, и обозначим полученную сумму Рj:
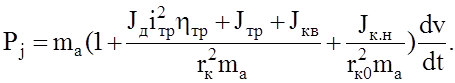(2.36)
Сила Рjа представляет собой приведенную силу инерции автомобиля, приложенную в его центре масс и эквивалентную силам инерции и инерционным моментам всех механизмов автомобиля при неустановившемся прямолинейном движении. Иными словами, сила Рja в рассматриваемых условиях движения эквивалентна совокупности силы инерции Рjп поступательно движущейся массы автомобиля и инерционных моментов Мjд, Мjтр, Мjк.н, Мjк.в масс, совершающих вращательные движения относительно корпуса автомобиля.
Введем обозначения:
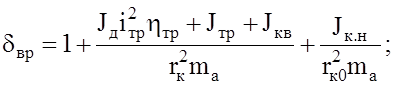(2.37)
(2.38)
Величину mа.пр называют приведенной массой автомобиля. Кинетическая энергия поступательного движения этой массы равна сумме кинетических энергий всех масс автомобиля в их действительных движениях.
Величина δвр называется коэффициентом учета вращающихся масс (приведенной массы) автомобиля. Коэффициент δвр учитывает влияние относительного вращательного движения масс двигателя, трансмиссии и колес на изменение кинетической энергии автомобиля. Он показывает, во сколько раз энергия, затрачиваемая на разгон масс реального автомобиля, больше энергии, необходимой для разгона поступательно движущегося твердого тела массой mа.
Учитывая выражения (2.37) и (2.38), дифференциальное уравнение движения автомобиля с механической трансмиссией можно записать в виде
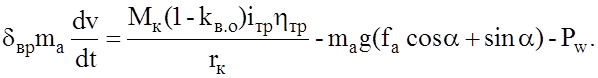(2.39)
Второе слагаемое правой части уравнения (2.39) характеризует суммарное сопротивление дороги (сопротивление подъему и сопротивление качению). При малых значениях α, характерных для автомобильных дорог с твердым покрытием, можно принять cosα=1, sinα=tgα=i и ввести обозначение
ψ=f+i, (2.40)
где ψ - коэффициент суммарного дорожного сопротивления.
Подставим значение Fw в уравнение (2.39), пренебрегая скоростью ветра, и получим дифференциальное уравнение движения автомобиля с механической трансмиссией:
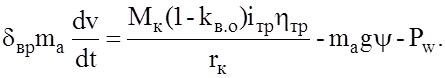(2.41)
Уравнение движения автомобиля (2.41) позволяет проанализировать влияние параметров автомобиля на характеристики движения и в конечном итоге дать оценку показателей его тягово-скоростных свойств в конкретных дорожных условиях.
При анализе движения автопоезда в уравнения (2.39) и (2.41) включается дополнительно сила сопротивления движению прицепа:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.