Моделирование хаотических динамических систем. Преобразование исходного ДУ к виду системы ДУ первого порядка

Санкт-Петербургский государственный технический университет Факультет Технической Кибернетики

Кафедра Компьютерных Систем и Программных Технологий

ЛАБОРАТОРНАЯ РАБОТА №3

Дисциплина: Моделирование систем управления

Тема: Моделирование хаотических динамических систем

Выполнил студент гр. 4081/1                          

Руководитель, к.т.н., доцент                            

"___ "_________ 2011 г.

Санкт-Петербург 2011

1.  Цель работы

Провести исследование хаотической системы в пакете Simulink.

2.  Программа работы

·  Преобразование исходного ДУ к виду системы ДУ первого порядка;

·  Построить в Simulink модели для исследования заданной системы;

·  Задать начальные условия для интеграторов, изходя из указанных начальных условий;

·  Промоделировать систему при различных значениях параметров.

Табл. 2.1. Индивидуальные параметры

·   

3.  Выполнение работы

3.1.  Преобразование исходного ДУ к виду системы ДУ первого порядка

3.2.  Получение модели в Simulink

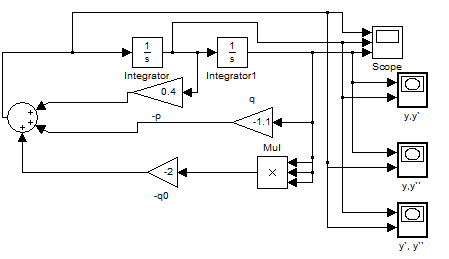
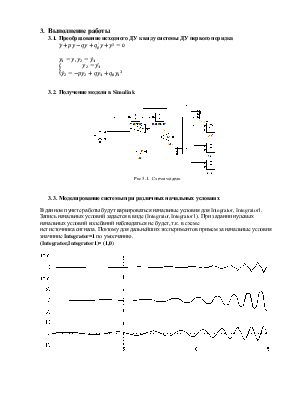
Рис 3.1. Схема модели

3.3.  Моделирование системы при различных начальных условиях

В данном пункте работы будут варьироваться начальные условия для Integrator, Integrator1. Запись начальных условий задается в виде (Integrator,Integrator1). При задании нулевых начальных условий колебаний наблюдаться не будет, т.к. в схеме нет источника сигнала. Поэтому для дальнейших экспериментов примем за начальные условия значиние Integrator=1 по умолчанию.

(Integrator,Integrator1)= (1,0)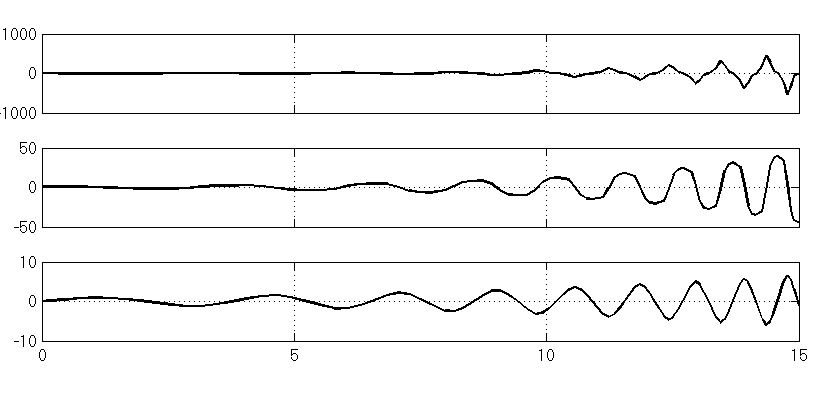

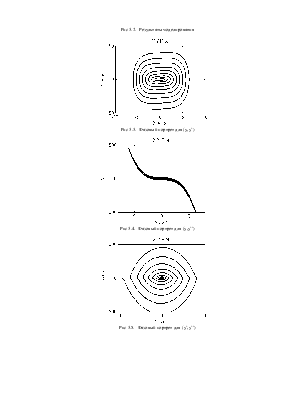
Рис 3.2. Результаты моделирования

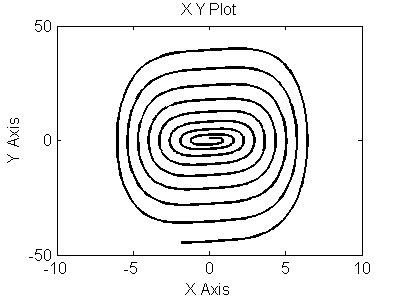
Рис 3.3. Фазовый портрет для (y,y`)

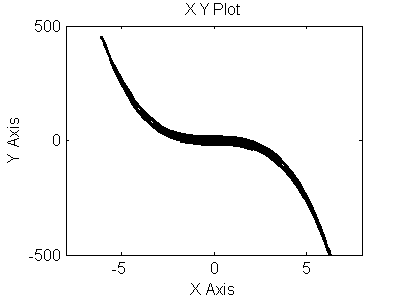
Рис 3.4. Фазовый портрет для (y,y``)

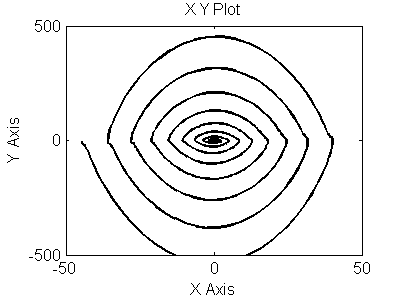
Рис 3.5. Фазовый портрет для (y`,y``)

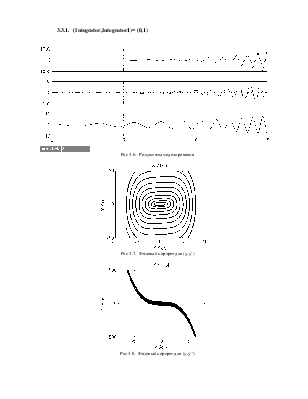
3.3.1.  (Integrator,Integrator1)= (0,1)

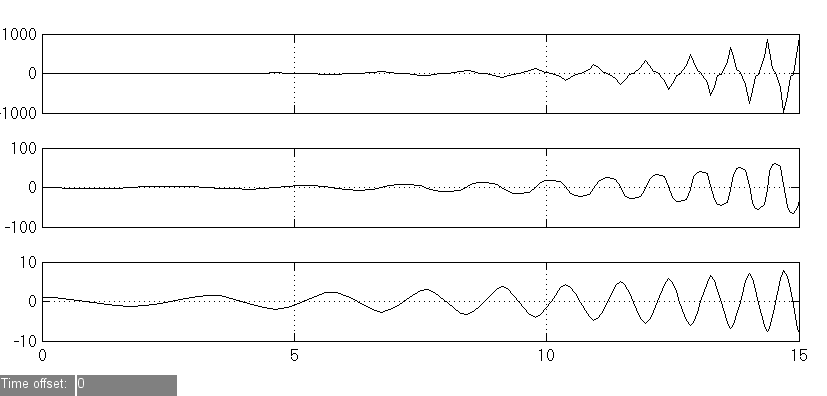
Рис 3.6. Результаты моделирования

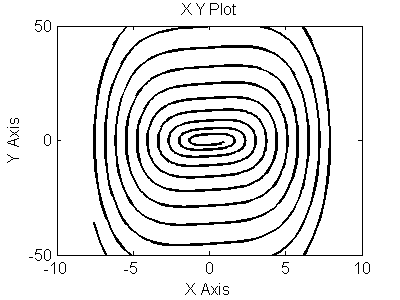
Рис 3.7. Фазовый портрет для (y,y`)

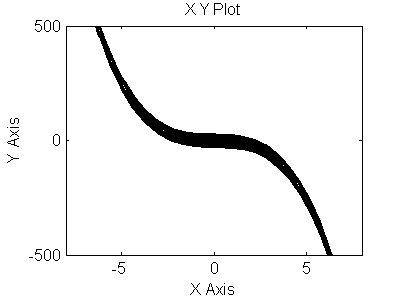
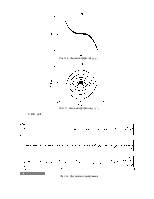
Рис 3.8. Фазовый портрет для (y,y``)

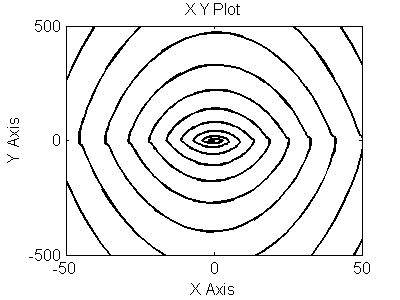
Рис 3.9. Фазовый портрет для (y`,y``)

3.4.  Моделирование системы при различных значениях параметров

В качестве изменяемого параметра выберем q0.

3.4.1.  q0=-2

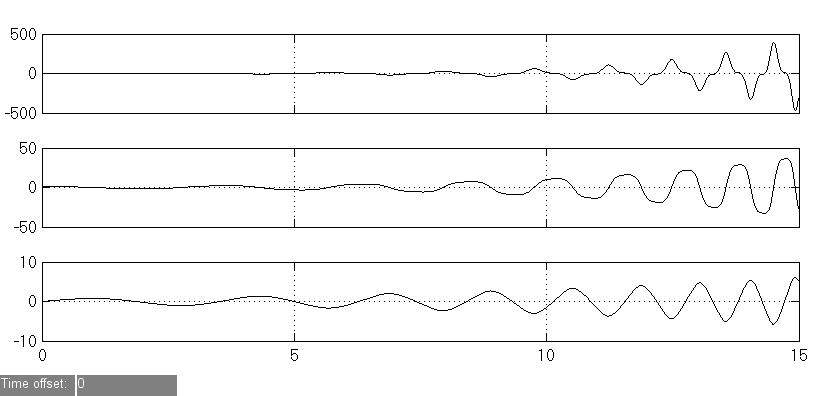
Рис 3.14. Результаты моделирования

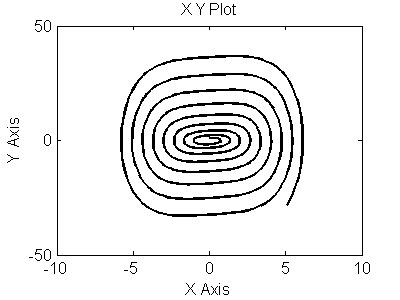
Рис 3.15. Фазовый портрет для (y,y`)

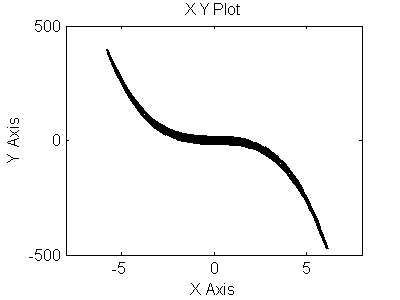
Рис 3.16. Фазовый портрет для (y,y``)

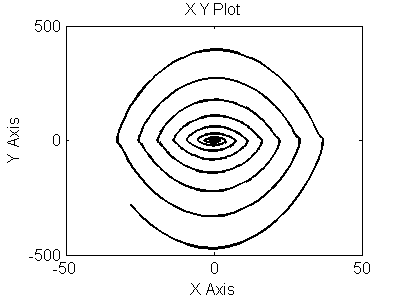
Рис 3.17. Фазовый портрет для (y`,y``)

3.4.2.  q=1

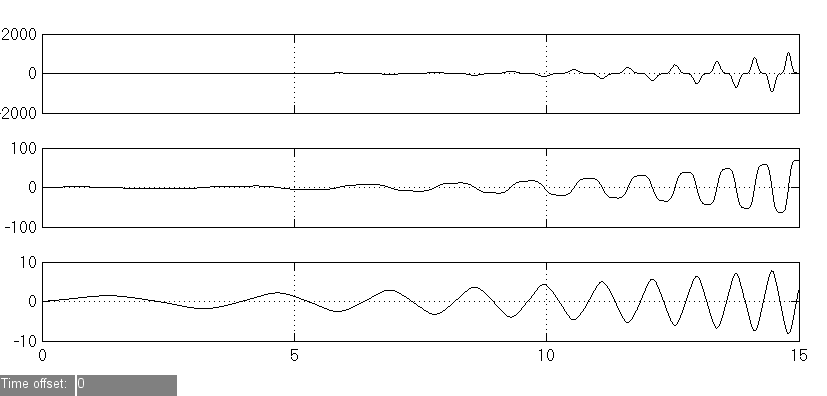
Рис 3.18. Результаты моделирования

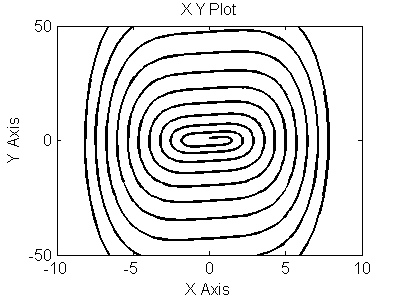
Рис 3.19. Фазовый портрет для (y,y`)

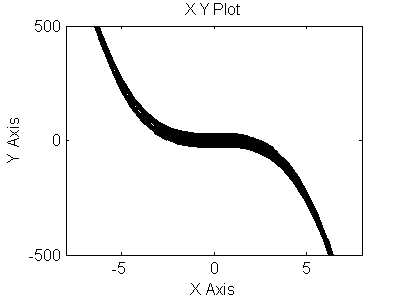
Рис 3.20. Фазовый портрет для (y,y``)

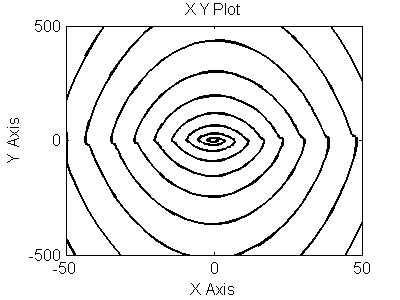
Рис 3.21. Фазовый портрет для (y`,y``)

При изменении параметра произошло изменение всех фазовых портретов, сигнал на выходе также изменился, стал чаще меняться.

Выводы

В данной работе была исследована динамическая система для получения хаотических колебаний на выходе. Исходное уравнение Дуффинга было преобразовано к виду Коши и построена модель исходного уравнения в пакете Simulink. Для исследования полученной  модели изменялись ее параметры и начальные условия, на выходе мы наблюдали измененение хаотического сигнала.