Санкт-Петербургский государственный технический университет Факультет Технической Кибернетики
Кафедра Компьютерных Систем и Программных Технологий
ЛАБОРАТОРНАЯ РАБОТА №1
Дисциплина: Моделирование систем управления
Тема: Моделирование линейных динамических систем
Выполнил студент гр. 4081/1
Руководитель, к.т.н., доцент
"___ "_________ 2011 г.
Санкт-Петербург 2011
Вариант №5:
Передаточная функция
исследуемого звена: ![]() (варьируем
K)
(варьируем
K)
1. Подготовительный этап
1.1. Перейти от записи системы в виде передаточной функции к записи в виде уравнений состояния:
- аналитически
![]()
![]() -
система уравнений состояния стационарной системы, где А – матрица состояния,В – матрица управления, С – матрица выхода по состоянию, D – матрица выхода по управлению,
Х – вектор состояния.
-
система уравнений состояния стационарной системы, где А – матрица состояния,В – матрица управления, С – матрица выхода по состоянию, D – матрица выхода по управлению,
Х – вектор состояния.
![]()
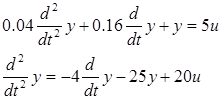
![]()
переменные состояния: ![]() ,
, ![]()
![]()
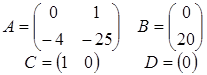
- с использованием Control System Toolbox
>> sys = tf(5, [0.04, 0.16, 1])
Transfer function:
5
---------------------
0.04 s^2 + 0.16 s + 1
>> sys_ss = ss(sys)
a =
x1 x2
x1 -4 -6.25
x2 4 0
b =
u1
x1 4
x2 0
c =
x1 x2
y1 0 7.813
d =
u1
y1 0
Continuous-time model.
Переход от передаточной функции к уравнениям состояния является неоднозначным, поэтому матрицы, полученные аналитически и с использованием Control System Toolbox, различаются.
1.2. Определить нули и полюса системы с использованием Control System Toolbox
>> pole(sys)
ans =
-2.0000 + 4.5826i
-2.0000 - 4.5826i
1.3. Построить в Simulink модель исследования колебательного звена второго порядка с заданными параметрами К, Т и z
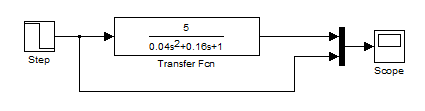
Рис 1.3. Схема набора модели
1.4. Написать скрипт на языке Matlab, который по данным переходного процесса будет определять показатели качества (перерегулирование, время переходного процесса, колебательность)
%Определение параметров качества переходного процесса
function [tp, sigma, koleb] = quality_dron( sys )
% [TP SIGMA X0] = quality( sys ), где sys - система управления,
% описанная функциями tf, ss, zpk возвращает значения времени
% переходного процесса, перерегулирования, колебательности
% переходного процесса в системе
sys = tf(5, [0.25, 0.7, 1]); % передаточная функция
%вычисляем полюса системы
p1 = pole(sys);
%вычисляем мнимые части полясов
p2 = imag(p1);
%вычисляем вещественные части полясов
pl = real(p1);
%проверка на правые полюса
if ( any(pl>0) ) return; end;
pl = -pl;
%вычисляем степень устойчивости
n = min(pl);
%вычисляем степень колебательности
k = min(p2);
koleb = tan(k/n);
%вычисляем время переходного процесса (приближенно)
tp = log(20) / n;
%вычисление перерегулирования
[y t] = step(sys);
xmax = Get1Maximum(y);
%вычисление установившегося значения
[y t] = step(sys, t(end)*100);
x0 = y(end);
%вычисляем перерегулирование
sigma = xmax/x0 - 1;
%вывод результатов в командное окно
tp = tp
sigma = sigma
koleb = koleb
return;
%поиск максимального подъема переходной характеристики
function h = Get1Maximum( x )
h = x(1);
for (i=2:length(x))
if ( x(i) >= h ) h = x(i);
else break;
end;
end;
return;
>> результаты
tp = 2.1398
sigma = 0.0460
koleb = -1.6289
ans = 2.1398
1.5. Определить передаточную функцию системы, полученной из заданной путем ее замыкания через единичную отрицательную обратную связь (ООС), перейти от записи системы в виде передаточной функции к записи в виде уравнений состояния, определить нули и полюса системы.
Для нахождения передаточной функции системы, полученной из заданной путем ее замыкания через единичную ОС, воспользуемся функцией feedback:
>> K=5;
>> T=0.04;
>> z=0.16;
>> func = tf( [K/T^2], [1 2*z/T 1/T^2] );
>> func_os = feedback( func, 1 )
Transfer function:
3125
---------------s^2 + 8 s + 3750
Переход от записи системы в виде передаточной функции к записи в виде уравнений состояния:
>> [A, B, C, D] = tf2ss( func_os.num{1}, func_os.den{1} )
A = -8 -3750
1 0
B = 1
0
C = 0 3125
D = 0
Поиск нулей системы:
>> matr = ss( A, B, C, D )
a = x1 x2
x1 -8 -3750
x2 1 0
b = u1
x1 1
x2 0
c = x1 x2
y1 0 3125
d = u1
y1 0
Continuous-time model.
Поиск полюсов системы:
>> pol = pole( ss_sys )
pol = -4.0000 +61.1065i
-4.0000 -61.1065i
1.6. Построить в Simulink модель для исследования полученной замкнутой системы с ООС
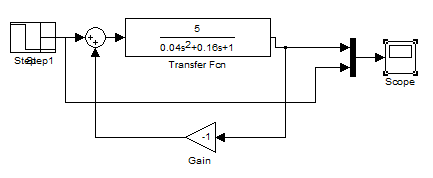
Рис 1.6. Схема набора модели с отрицательной ОС
2. Моделирование временных характеристик звена
2.1. Построить переходную функцию звена с использованием Simulink и Control System Toolbox
>> sys = tf(5, [0.25, 0.7, 1]);
>> step(sys)
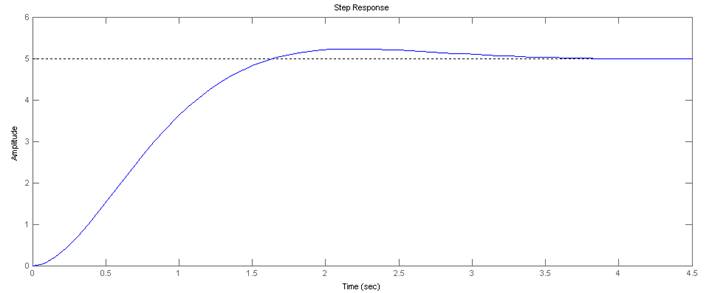
Рис 2.1.1. Переходная характеристика в Control System Toolbox
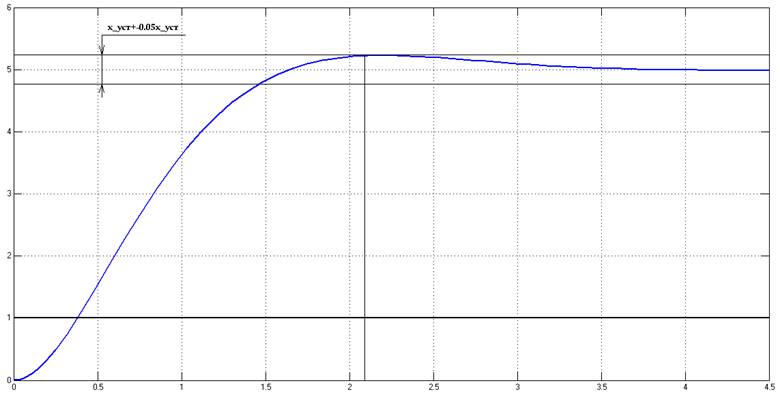
Рис 2.1.2. Переходная характеристика в Simulink
2.2. По переходной характеристике определить показатели качества переходного процесса
Быстродействие (время переходного процесса): 2.13 сек (см. Рис 2.1.2)
Перерегулирование:
![]()
Колебательность = число колебаний выходной величины за время переходного процесса = 1
2.3. Исследовать влияние заданного параметра (K) на вид переходной функции
Функция размещает графики переходных функций для различных z на одном рисунке:
function f = step_sys(sys)
sys1 = tf(5, [0.16, 0.04, 1]);
step(sys1)
hold on;
sys2 = tf(5*0.1, [0.16, 0.04, 1]);
step(sys2)
hold on;
sys3 = tf(5*0.5, [0.16, 0.04, 1]);
step(sys3)
hold on;
sys4 = tf(5*2, [0.16, 0.04, 1]);
step(sys4)
hold on;
sys5 = tf(5*5, [0.16, 0.04, 1]);
step(sys5)
hold on;
sys6 = tf(5*10, [0.16, 0.04, 1]);
step(sys6)
hold on;
grid on;
legend('10%z','50%z','100%z','150%z','200%z','1000%z');
return;
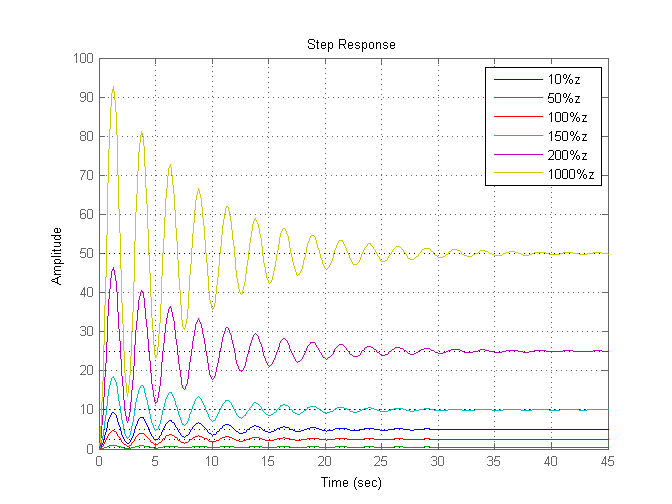
Рис 2.3. Переходная характеристика для различных K
Легко заметить, что изменение К не влияет на исследуемые показатели качества переходного процесса. Пропорционально изменению К меняется установившееся значение (собственно, оно равно К).
2.5. Построить весовую функцию звена с использованием Simulink и Control System Toolbox
>> sys = tf(5, [0.04, 0.16, 1]);
>> impulse(sys)
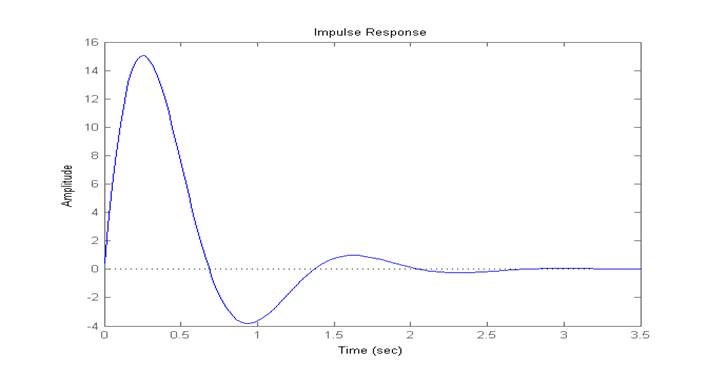
Рис 2.5.1. Весовая функция в Control System Toolbox
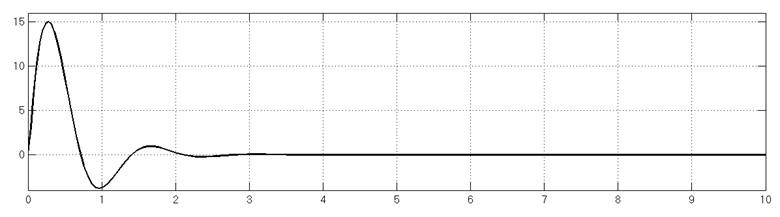
Рис 2.5.2. Весовая функция в Simulink
2.6. Исследовать влияние заданного параметра на вид весовой функции
Функция размещает графики весовых функций для различных z на одном рисунке:
function f = impulse_sys(sys)
sys1 = tf(5, [0.25, 0.7*0.1, 1]);
impulse(sys1)
hold on;
sys2 = tf(5, [0.25, 0.7*0.5, 1]);
impulse(sys2)
hold on;
sys3 = tf(5, [0.25, 0.7, 1]);
impulse(sys3)
hold on;
sys4 = tf(5, [0.25, 0.7*1.5, 1]);
impulse(sys4)
hold on;
sys5 = tf(5, [0.25, 0.7*2, 1]);
impulse(sys5)
hold on;
sys6 = tf(5, [0.25, 0.7*10, 1]);
impulse(sys6)
hold on;
grid on;
legend('10%z','50%z','100%z','150%z','200%z','1000%z');
return;
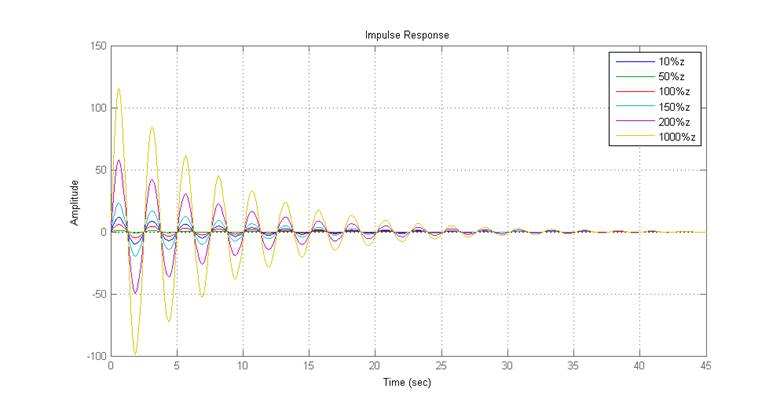
Рис 2.6. Весовые функции для различных K
Так же, как и в случае с переходными характеристиками, изменение параметра K не влияет на показатели качества.
3. Моделирование частотных характеристик звена
3.1. Построить частотные характеристики (АЧХ и ФЧХ) с использованием Control System Toolbox
>> sys = tf(5, [0.04, 0.16, 1]);
>> bode(sys)
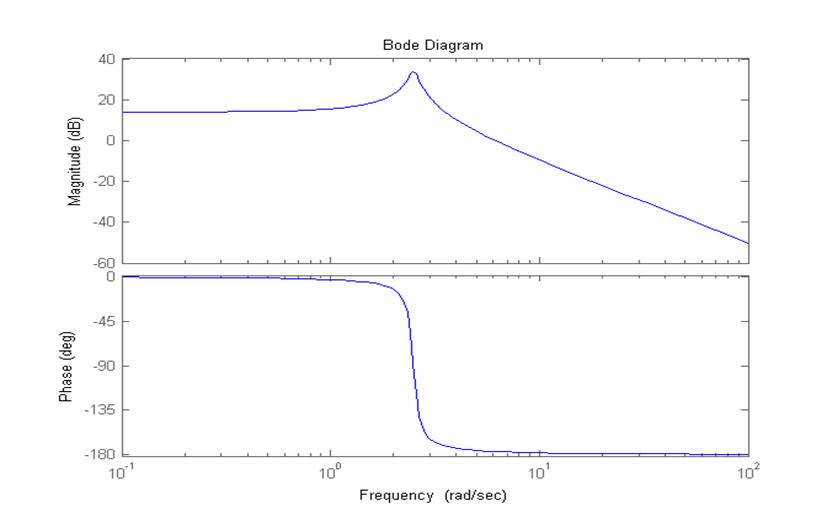
Рис 3.1. АЧХиФЧХв Control System Toolbox
3.2. Исследовать влияние заданного параметра (K) на вид частотных характеристик
Функция, размещающая графики АЧХ и ФЧХ для различных K на одном рисунке, аналогична представленным выше функциям.
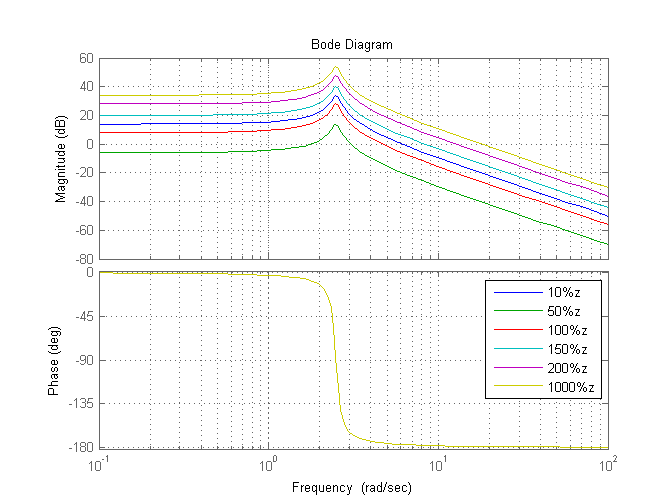
Рис 3.2. АЧХ и ФЧХ для различных K
Заметим, что изменение коэффициента усиления не оказывает влияния на вид фазовой частотной характеристики. Данный параметр влияет только на уровень, на котором проходит амплитудная частотная характеристика.
3.3. Построить АФЧХ с использованием Control System Toolbox
>> sys = tf(5, [0.25, 0.7, 1]);
>> nyquist(sys)
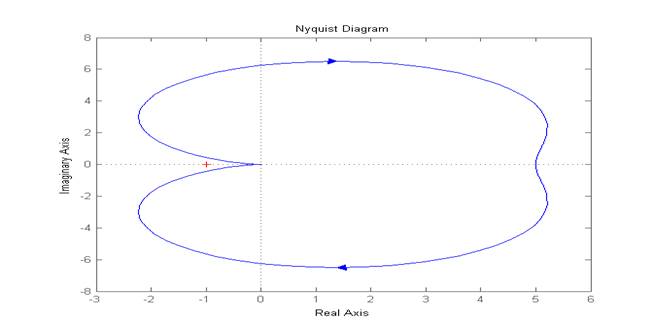
Рис 3.1. АФЧХв Control System Toolbox
3.4. Исследовать влияние заданного параметра (z) на вид АФЧХ
Функция, размещающая графики АФЧХ для различных K на одном рисунке
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.