Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Компьютерных Систем и Программных Технологий
Отчет
по лабораторной работе №4
Моделирование стохастических динамических систем
Моделирование систем управления
Работу выполнила:
группа 4081/11
Преподаватель: .
Подпись преподавателя:___________________
Санкт-Петербург
2011
Вариант №12:
|
T1 |
T2 |
K1 |
K2 |
Kos |
C |
d1 |
d2 |
Ку |
|
|
|
0.04 |
0.25 |
5 |
8 |
0.5 |
1.6 |
0.3 |
0.8 |
0.5 |
0.4 |
0.2 |
1. Подготовительный этап
1.1. Написать скрипт на языке Matlab, который по данным процесса на выходе системы будет определять характеристики случайного процесса (математическое ожидание и дисперсию)
Формулы
для вычисления: математического ожидания: 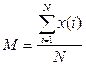 ,
дисперсии:
,
дисперсии: ![]() .
.
function [M,D] = findMD( X );
M = mean( X )
D = std( X ).^2
return;
Результаты моделирования белого шума (использовали блок Band-Limited White Noise):
>> findMD(shym)
M = 0.0031
D = 1.0009
2. Исследовать реакцию системы на нормальный случайный процесс
2.1. Исследовать реакцию системы на нормальный случайный
процесс (белый шум): ![]()
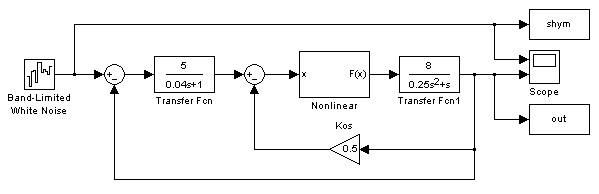
Рис 2.1.1. Схема набора исследуемой системы
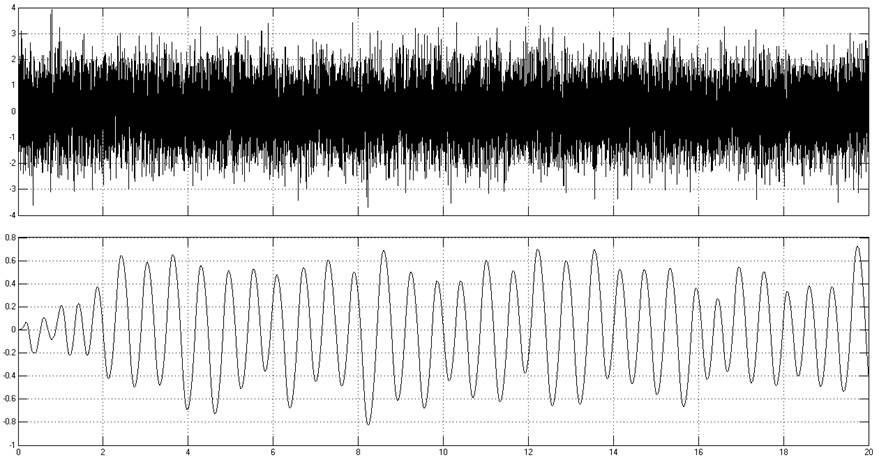
Рис 2.1.2. Осциллограммы входного и выходного сигналов
Параметры входного сигнала: M = -0.000063, D = 0.988888, выходного сигнала: M = -0.001531, D = 0.145139.
2.2. Исследовать влияние математического ожидания и дисперсии входного сигнала на выходной сигнал:
|
|
|
|
|
0 |
0.001531 |
0.145139 |
|
1 |
0.892494 |
0.157551 |
|
2 |
1.792294 |
0.188421 |
|
3 |
2.688120 |
0.239240 |
|
4 |
3.583264 |
0.323140 |
|
5 |
4.479441 |
0.443398 |
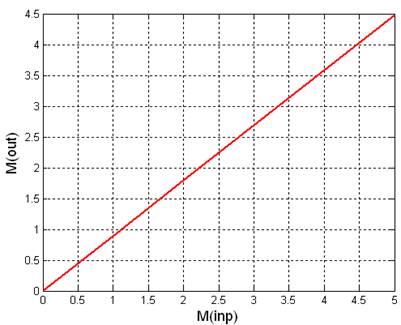
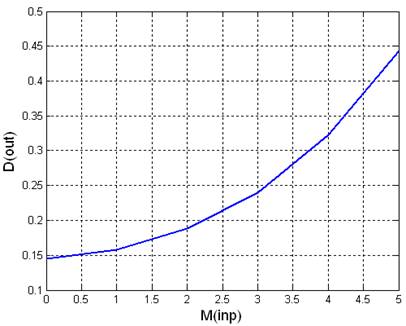
Рис 2.2.1. Графики зависимостей математического ожидания и дисперсии выходного сигнала от математического ожидания входного сигнала
|
|
|
|
|
0.2 |
0.024899 |
0.270530 |
|
0.5 |
0.010335 |
0.483812 |
|
1 |
0.008895 |
0.598695 |
|
2 |
0.050999 |
0.791531 |
|
3 |
0.022822 |
0.942146 |
|
4 |
0.020883 |
1.171229 |
|
5 |
0.026206 |
1.416452 |
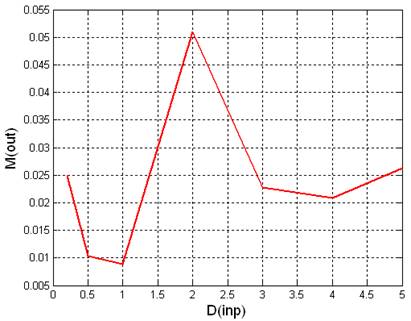
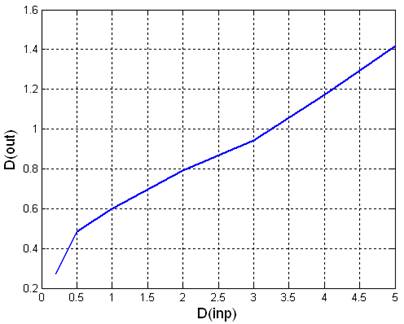
Рис 2.2.2. Графики зависимостей математического ожидания и дисперсии выходного сигнала от дисперсии входного сигнала
3. Исследовать реакцию системы на коррелированный случайный процесс
3.1. Сформировать блок-подсистему, реализующую
преобразование случайного процесса с помощью дискретного фильтра по методу
скользящего суммирования для получения нормального случайного процесса с
корреляционной функцией ![]() .
.
Чтобы преобразовать белый шум в случайный процесс с заданной корреляционной функцией, будем использовать метод скользящего суммирования:
![]() - нормальный случайный процесс
- нормальный случайный процесс
![]() - случайный процесс, который
необходимо сформировать
- случайный процесс, который
необходимо сформировать
Коэффициенты
разностного уравнения находятся из следующей системы: 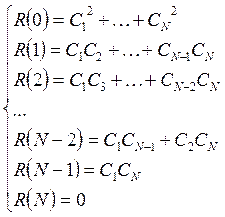
% Скрипт в Matlab для системы из пяти уравнений
sigma = 0.4;
alpha = 0.2;
deltat = 4;
% Корреляционная функция
K0 = sigmag^2 * exp( -alpha*0*deltat );
K1 = sigmag^2 * exp( -alpha*1*deltat );
K2 = sigmag^2 * exp( -alpha*2*deltat );
K3 = sigmag^2 * exp( -alpha*3*deltat );
K4 = sigmag^2 * exp( -alpha*4*deltat );
% Решение системы
syms c1 c2 c3 c4 c5;
s5 = c1*c5 – K4;
s4 = c1*c4 + c2*c5 – K3;
s3 = c1*c3 + c2*c4 + c3*c5 – K2;
s2 = с1*с2 + с2*с3 + с3*с4 + с4*с5 - K1;
s1 = с1^2 + с2^2 + с3^2 + с4^2 + с5^2 - K0;
S = solve( s1,s2,s3,s4,s5,c1,c2,c3,c4,c5 );
В результате решения системы получаем массив из 64 коэффициентов, из него выбираем значения, на основании которых синтезируем подсистему (подставляем полученные значения в блоки Gain на рисунке 3.1)
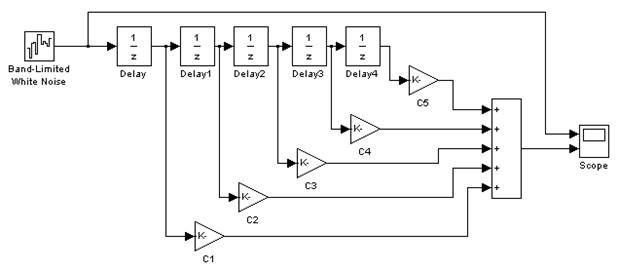
Рис 3.1. Синтезированная модель для исследования
3.2. Построить график оценки корреляционной функции случайного процесса, полученного на выходе построенной подсистемы. Сравнить с графиком заданной корреляционной функции
Для этого добавим в схему, изображенную на рисунке 3.1 блок ToWorkspace, с помощью которого будем получать выходное значение системы (out) и использовать его в представленном ниже скрипте.
% Заданная корреляционная функция
sigma = 0.4; alpha = 0.2;
t = -20:0.01:20;
R = sigma^2 * exp( -alpha*abs(t) );
plot( t, R );
hold on;
% Корреляционная функция случайного процесса, полученного на выходе построенной подсистемы
R = xcorr(out)/length(out);
tau = -20:Tp:20;
lt = length( tau );
s1r = round(length(R)/2)-lt/2;
s2r = round(length(R)/2)+lt/2-1;
plot( tau, R(s1r:s2r) );
grid on;
Результаты моделирования:
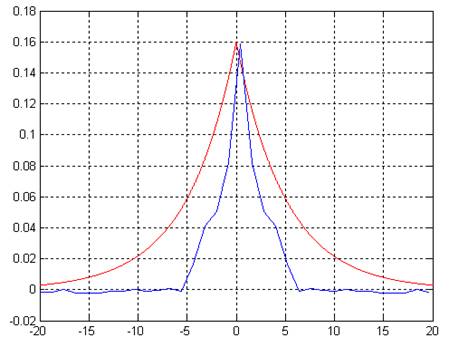
Рис 3.2. Заданная корреляционная функция (красный график) и ее оценка (синий)
3.3. Исследовать реакцию системы на нормальный случайный процесс с данной корреляционной функцией
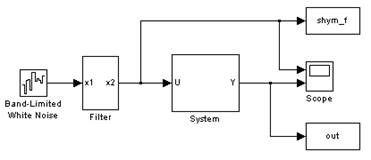
Рис 3.3.1. Модель для исследования в Simulink
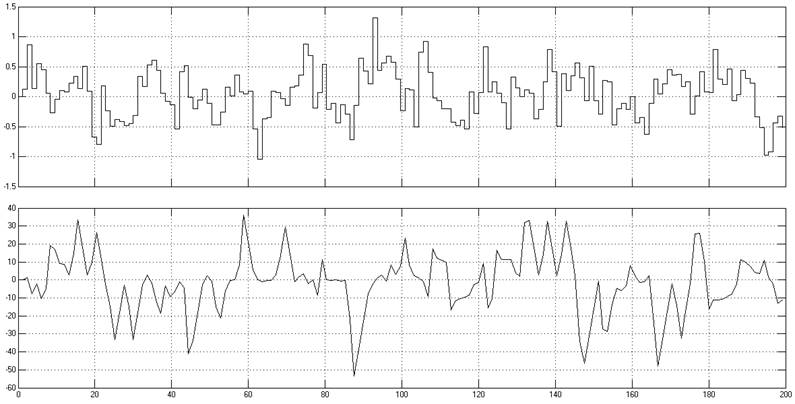
Рис 3.3.2. Снятые осциллограммы в Simulink: входной отфильтрованный сигнал и выходной сигнал
|
|
|
|
|
0 |
-0.116159 |
250.567828 |
|
1 |
0.658607 |
251.198340 |
|
2 |
2.558266 |
242.738447 |
|
3 |
2.428229 |
237.146421 |
|
4 |
3.744880 |
252.940122 |
|
5 |
4.266708 |
257.150833 |
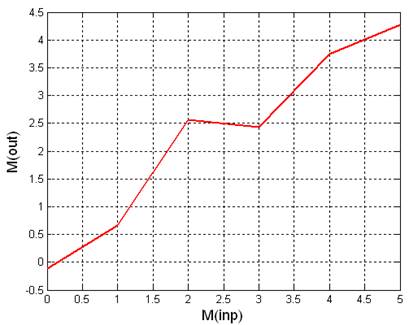
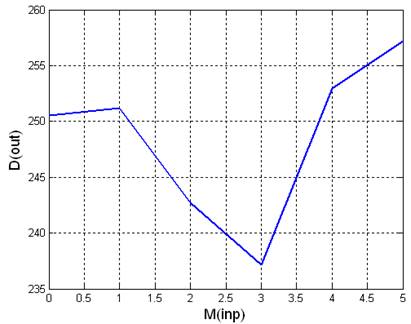
Рис 3.3.3. Графики зависимостей математического ожидания и дисперсии выходного сигнала от математического ожидания входного сигнала
|
|
|
|
|
0.2 |
-3.758841 |
135.319673 |
|
0.4 |
0.808303 |
227.404094 |
|
0.5 |
0.249562 |
233.707178 |
|
0.7 |
0.420329 |
251.477897 |
|
0.9 |
0.313443 |
248.317473 |
|
1 |
0.329484 |
247.050105 |
|
2 |
-0.318222 |
257.482268 |
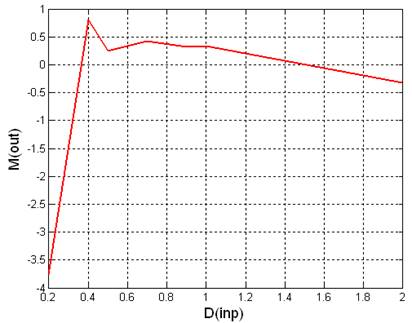
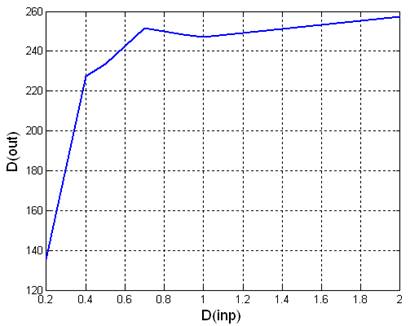
Рис 3.3.4. Графики зависимостей математического ожидания и дисперсии выходного сигнала от дисперсии входного сигнала
4. Исследовать прохождение случайного процесса через линейную систему
4.1. Заменить нелинейный элемент блоком масштабирования с
коэффициентом усиления ![]() .
.
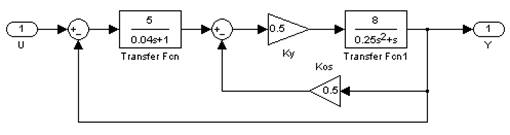
Рис 4.1. Структурная схема линейной системы
4.2. Рассчитать дисперсию сигнала на выходе системы при подаче на вход нормального случайного процесса (белого шума)
Дисперсию сигнала при подаче на вход нормального случайного процесса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.