Коэффициенты прямых материальных затрат. Объемы конечной продукции. Изменение удельной условно-чистой продукции, страница 4

Отрасль	А	Б	В	Г	∑	Y	X
А	115,075	230,865	88,09	117,485	551,515	1750	2301,52
Б	552,36	153,91	176,18	195,8	1078,25	2000	3078,26
В	690,45	307,82	308,31	97,9	1404,48	3000	4404,503
Г	828,54	461,73	0	146,85	1437,12	1500	2937,135
∑	2168,425	1154,325	572,58	558,035	4471,365
Z	115,092	1923,935	3831,923	2379,1
X	2301,52	3078,26	4404,503	2937,135

Задание 3

В матричном виде модель межотраслевого баланса имеет вид:

 ,где

X – матрица-столбец объемов валовой продукции отраслей;

Y – матрица-столбец объемов конечной продукции отраслей;

A – матрица коэффициентов прямых материальных затрат.

Матричное решение:

Обозначим матрицу                 как матрицу B

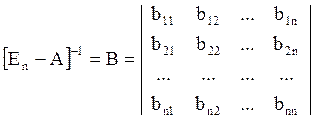
Теперь                или в матричном виде: X=B*Y.

X=B*Y представляет собой модель объемов выпуска. Эта модель дает выражение объемов валовой продукции отраслей через объемы конечной продукции и числа b_ij.

Коэффициенты b_ij называются коэффициентами полных материальных затрат и показывают количество валовой продукции, которое необходимо произвести i-ой отрасли, чтобы обеспечить выпуск единицы конечной продукции входит в b_ij, поскольку включаются не только прямые затраты, но и косвенные.

B =

Домножим обе части уравнения на матрицу

 

Обозначим     , тогда получим       или в индексной форме:

          ,          

Это соотношение позволяет получить n систем уравнений для нахождения компонентов матрицы B (коэффициентов b_ij): каждая система для нахождения элементов одного столбца матрицы:

                                             система уравнений для

 нахождения 1-го столбца

матрицы B

	система уравнений для нахождения 2-го столбца матрицы B

 

Найдем элементы матрицы С ([E_n-A]=C) для заданных условий:

0,05   0,15   0,04   0,12                      0,95   -0,15   -0,04   -0,12

А =     0,12   0,05   0,04   0,10     =>  C =   -0,12    0,95   -0,04   -0,10

0,15   0,10   0,07   0,05                     -0,15   -0,10    0,93   -0,05

0,12   0,10   0,00   0,05                     -0,12   -0,10   0,00     0,95

 

0,95b₁₁-0,15b₂₁-0,04b₃₁-0,12b₄₁=1

-0,12b₁₁+0,95b₂₁-0,04b₃₁ – 0,10b₄₁=0

-0,15b₁₁-0,10b₂₁+0,93b₃₁-0,05b₄₁=0

-0,12b₁₁-0,10b₂₁+0,95b₄₁=0

 

0,95b₁₂-0,15b₂₂-0,04b₃₂-0,12b₄₂=0

-0,12b₁₂+0,95b₂₂-0,04b₃₂ – 0,10b₄₂=1

-0,15b₁₂-0,10b₂₂+0,93b₃₂-0,05b₄₂=0

-0,12b₁₂-0,10b₂₂+0,95b₄₂=0

 

0,95b₁₃-0,15b₂₃-0,04b₃₃-0,12b₄₃=0

-0,12b₁₃+0,95b₂₃-0,04b₃₃ – 0,10b₄₃=0

-0,15b₁₃-0,10b₂₃+0,93b₃₃-0,05b₄₃=1

-0,12b₁₃-0,10b₂₃+0,95b₄₃=0

 

0,95b₁₄-0,15b₂₄-0,04b₃₄-0,12b₄₄=0

-0,12b₁₄+0,95b₂₄-0,04b₃₄ – 0,10b₄₄=0

-0,15b₁₄-0,10b₂₄+0,93b₃₄-0,05b₄₄=0

-0,12b₁₄-0,10b₂₄+0,95b₄₄=1

Значения полных материальных затрат (b_ij), найденные по методу Гаусса:

1,1071   0,1979   0,0561   0,1636

В =     0,1649   1,099      0,0544   0,1394

0,2048   0,1577   1,0909    0,0999

0,1572   0,1407    0,0129   1,088

Задание 4

Перемножим матрицу B и Y, это позволит найти точные значения объемов выпуска продукции отраслей:

 

1,1071   0,1979   0,0561   0,1636                  300                     460,255

0,1649   1,099      0,0544   0,1394     *          200      =             307,775

0,2048   0,1577   1,0909    0,0999                300                     440,48