Коэффициенты прямых материальных затрат. Объемы конечной продукции. Изменение удельной условно-чистой продукции, страница 2

X₂=0,12 x₁ +0,05 x₂ +0,04 x₃ +0,10 x₄ +200;

X₃=0,15 x₁ +0,10 x₂ +0,07 x₃ +0,05 x₄ +300;

X₄=0,12 x₁ +0,10 x₂ +0,05 x₄ +100.

Поскольку экономико-математическая модель МОБ сводится к системе уравнений из n-линейных уравнений (в данном случае из четырех), то к ней применимы обычные методы решения этих систем, которые можно разделить на точные (прямые) и итерационные (приближенные).

Прямые методы позволяют найти точное решение за конечное число шагов.

Итерационные методы теоретически также позволяют найти точное решение, но число шагов при этом должно быть равно бесконечности. В приближенных методах каждый шаг приближающий к решению называется итерацией.

В любом итерационном или приближенном методе решение начинается с изобретения начального или нулевого приближения к решению. В методе межотраслевого баланса начальное приближение – это объемы конечной продукции, т. е. нулевым приближением будет являться:

X_i⁽⁰⁾=Y_i

Суть итерационного метода заключается в последовательном приближении к точному решению. По известным x⁽⁰⁾ определяем первое приближение, т. е. улучшенное решение:

1.  Для метода простой итерации:

X₁⁽¹⁾=a₁₁x₁⁽⁰⁾+a₁₂x₂⁽⁰⁾+…+a_1nx_n⁽⁰⁾+Y₁;

X₂⁽¹⁾=a₂₁x₁⁽⁰⁾+a₂₂x₂⁽⁰⁾+…+a_2nx_n⁽⁰⁾+Y₂;

………………………………………

X_n⁽¹⁾=a_n1x₁⁽⁰⁾+a_n2x₂⁽⁰⁾+…+a_nnx_n⁽⁰⁾+Y_n.

По первому приближению – второе и т. д.

Алгоритм матричный: X^(k)=AX^(k-1)+Y.

Решение будет продолжаться до тех пор, пока не будет выполнено следующее условие: |X_i^(k)-X_i^(k-1)| ≤ ε, i=1,n.

ε – некое малое наперед заданное число.

Чем меньше величина  ε, тем большее число итераций требуется для выполнения последнего условия, тем точнее расчет.

Решение идет с точность до ε.

2.  Для метода Зейделя:

X₁⁽¹⁾=a₁₁x₁⁽⁰⁾+a₁₂x₂⁽⁰⁾+a₁₃x₃⁽⁰⁾+…+a_1nx_n⁽⁰⁾+Y₁;

X₂⁽¹⁾=a₂₁x₁⁽¹⁾+a₂₂x₂⁽⁰⁾+a₂₃x₃⁽⁰⁾+…+a_2nx_n⁽⁰⁾+Y₂;

X₃⁽¹⁾=a₃₁x₁⁽¹⁾+a₃₂x₂⁽¹⁾+a₃₃x₃⁽⁰⁾+…+a_3nx_n⁽⁰⁾+Y₃;

………………………………………………….

X_n⁽¹⁾=a_n1x₁⁽¹⁾+a_n2x₂⁽¹⁾+a_n3x₃⁽¹⁾+…+a_nnx_n⁽⁰⁾+Y_n.

Аналогично определяется 2, 3, ……, k – приближение. Решение продолжается до тех пор, пока не будет выполнено условие: |X_i^(k)-X_i^(k-1)| ≤ ε, i=1,n.

Систему уравнений (1) решим при помощи компьютера итерационными методами..

Вычисляя по методу простой итерации, получаем следующие значения валовой продукции:

Из таблицы видно, что необходимые значения найдены за 25 итераций.

Вычисляя по методу Зейделя, получаем следующие значения валовой продукции:

Из таблицы видно, что необходимые значения объема валовой продукции найдены за 23 итерации.

Изобразим графически зависимость количества итераций от точности расчета.

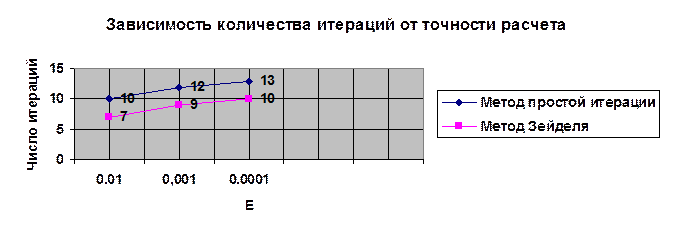
Таким образом, можно сделать вывод, что необходимые значения объемов конечной продукции методом Зейделя были найдены за меньшее число итераций (9), чем методом простых итераций (12).

В нашей задаче это условие выполняется при ε = 0,001. Использование метода Зейделя дает следующие значения:

X₁ =460,3044

X₂ =307,8268

X₃ =440,4504

X₄ =195,8097

Задание 2

Межотраслевой баланс можно представить в виде таблицы, где каждая отрасль представлена дважды.

Представленная строкой отрасль выступает как поставщик продукции всем отраслям, включая себя.

Представленная столбцом отрасль выступает как потребитель, включая себя саму.