Разработка системы связи для передачи дискретных сообщений. Алфавит источника сообщений с вероятностями символов

средняя длина кодовой комбинации для построенного кода

μ_ср=0.167·3+0.131·3+0.102·3+0.102·3+0.092·3+0.085·4+0.074·4+0.067·4+

+0.064·4+0.064·5+0.028·5+0.026·5+0.014·6+0.014·6=3.7

Согласно теореме Шеннона при кодировании можно достичь средней длины

μ_min=H(A)/log₂2=H(A)=3.6

μ_ср≠μ_min

Таким образом, построенный код не является оптимальным.

Вероятность появления нуля (априорная вероятность)

p₀=0.445

Вероятность появления единицы

р₁=1-р₀=1-0.445=0.555

Значит, энтропия кода

H_K=-(p₀log₂p₀+p₁log₂p₁)

H_K=-(0.445log0.445+0.555log0.555)=0.99125 бит

Избыточность кода

где H_Kmax=log₂m=log₂2=1

Скорость передачи информации по каналу без помех

где τ=0.7·10^-6с – длительность посылки.

6.  Описание процесса принятия приемником решения

 при приеме сигнала.

В системах передачи информации с пассивной паузой, использующих бинарный код, задача анализа сигнала сводится к тому, что решающее устройство должно определить есть сигнал (принята «1») или нет (принят «0»).

Модулированный сигнал u(t), проходя через канал связи, подвергается воздействию помехи. На выходе получаем сигнал z(t), который является смесью переданного сигнала с помехой (z(t)=u(t)+η(t)).Задача демодулятора состоит в том, чтобы по наблюдаемому колебанию z(t) принять решение о переданном сигнале, такое, чтобы обеспечить максимальную верность. Правило принятия решения – это закон преобразования z(t) в b_ц(t).

При приеме сигнала используется пороговый обнаружитель. Принимаемая смесь сигнала с шумом z(t), сравнивается с определенным порогом z_п и, если происходит превышение порога, то считается, что передана «1», иначе «0».

Из-за помех приемник может дать ошибочный результат, и вместо передаваемого символа мы получим другой. Эти ошибки можно классифицировать: 

1.  Ошибка первого рода (ложная тревога): при передаче элемента 0 принято решение о том, что передан   элемент  1; условная вероятность такого события обозначается  p₀₁.

2.  Ошибка второго рода (не обнаружение сигнала): при передаче элемента 1 принято решение о том, что передан   элемент  0; условная вероятность такого события обозначается  p₁₀.

Тогда средняя вероятность ошибки p_ош=p₀·p₁₀+p₁·p₀₁.

В данном задании помеха аддитивная и представляет собой  гауссовский белый шум с нулевым математическим ожиданием. Он характеризуется нормальной плотностью распределения вероятности

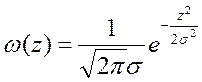
где σ² – дисперсия шума.

Гипотеза – предположение о передаваемом сигнале. Пусть гипотеза Н₀ – посылки нет (“0”), гипотеза Н₁ – посылка есть (“1”).

Далее рассматривается распределение случайной величины z в зависимости от того, есть ли сигнал (ω(z|H₁), (распределение при гипотезе Н₁) или нет (ω(z|H₀)-распределение при гипотезе Н₀. 

     

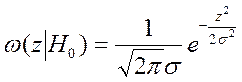
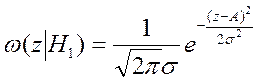
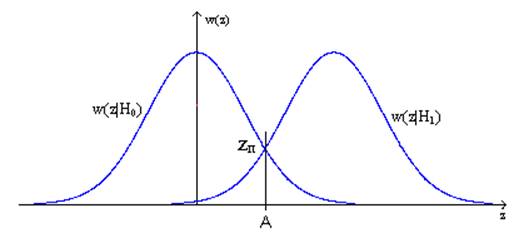
Рис.3 Условные плотности распределения вероятности

при наличии (ω(z|H₁)) и отсутствии (ω(z|H₀)) сигнала.

Оптимальный порог z_п находится в точке пересечения графиков распределения плотности вероятности.

7. Расчет характеристик системы согласно п.1.2.3.

7.1. Когерентный прием.

Когерентный прием – прием сигнала при условии, что форма сигнала на интервале наблюдения точно известна, неизвестен лишь сам факт наличия или отсутствия сигнала в наблюдаемом колебании.

Плотность распределения вероятности (ПРВ) в отсутствии сигнала

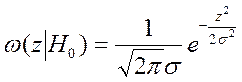
ПРВ при наличии сигнала

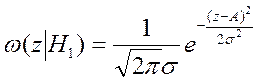
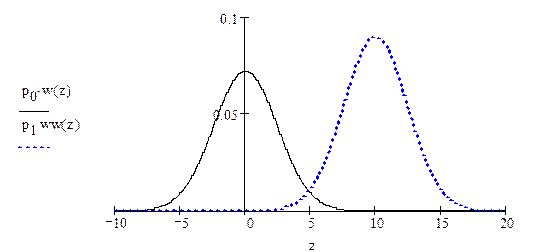
Рис4. Графики функций плотностей вероятности для мгновенных значений сигнала  z.

Оптимальный порог по критерию идеального наблюдателя (когда потери, связанные с различными ошибками, принимаются равными друг другу, приемник обеспечивает минимальную среднюю вероятность ошибки р_ош) определяем как точку пересечения графиков р₀ ω(z|H₀) и р₁ ω(z|H₁)

z_п=4.97

Вероятность ошибки первого рода определяется выражением

   

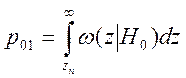
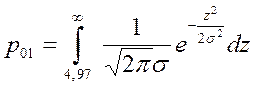
р₀₁=0.021

Вероятность ошибки второго рода

 

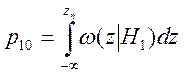
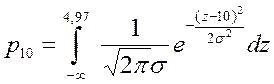
р₁₀=0.02

Тогда средняя вероятность ошибки согласно критерию идеального наблюдателя

 , i≠j

В нашем случае всего два символа 0 и 1, значит, i  и j принимают значения либо 0 либо 1.

р_ош=р₀р₀₁+р₁р₁₀

р_ош=0.445∙0.021+0.555∙0.02=0.02

Скорость передачи информации

где I(X,Y) – взаимная информация.

где p(x_i,y_i)=p(x_i)p(y_i|x_i) – совместная вероятность,

p(y_i|x_i) – условная вероятность.

В нашем случае существуют четыре совместные вероятности: р(1,0)=р₁р₁₀=0,0111

р(1,1)=р₁р₁₁=0,549

р(0,0)=р₀р₀₀=0,441

р(0,1)=р₀р₀₁=0,0093

где р₀₀=1-р₀₁=0,9906

р₁₁=1-р₁₀=0,9889

Вероятность того, что на выходе будет 0: р(y=0)=p₁₀p₁+p₀₀p₀=0.552

На выходе – 1: p(y=1)=p₁p₁₁+p₀p₀₁=0.5583

Тогда

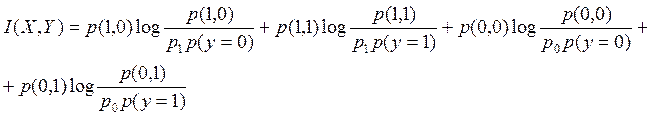
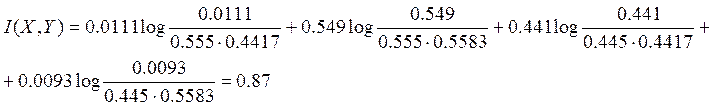
Тогда, скорость передачи информации

7.2 Некогерентный прием.

Некогерентный прием – прием сигнала, параметры которого известны не полностью, в частности, рассматривается задача приема сигнала со случайной начальной фазой.

ПРВ в отсутствии сигнала

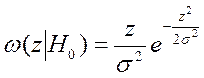
ПРВ при наличии сигнала

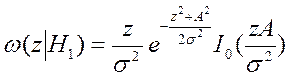
где I₀ – модифицированная функция Бесселя нулевого порядка

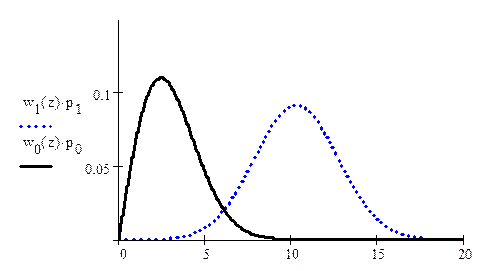
Рис.5 Графики ПРВ при некогерентном приеме.

Оптимальный порог определяем как точку пересечения плотностей распределения вероятностей.

z_п=6.13

Вероятность ошибки первого рода

    

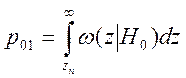
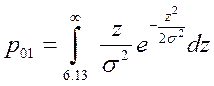
р₀₁=0,044

Вероятность ошибки второго рода

     

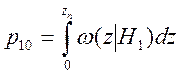
р₁₀=0,041

Тогда средняя вероятность ошибки

р_ош=р₀р₀₁+р₁р₁₀

р_ош=0,042

Скорость передачи информации при некогерентном приеме вычисляем аналогично когерентному приему

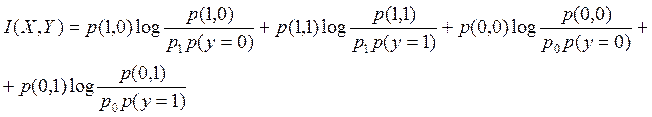
Преобразовав, получим

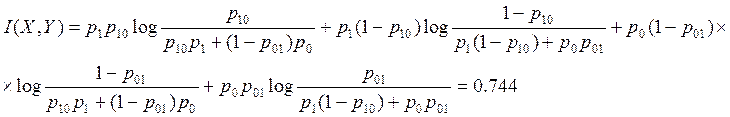
Тогда

Сравним результаты, полученные при когерентном и некогерентном приемах.

Таблица 2.

Способ приема	Вероятность ошибки первого рода р01	Вероятность ошибки второго рода р10	Средняя вероятность ошибки рош	Скрость передачи информации V(X,Y)
Когерентный	0.021	0.02	0.02	1.24·106бит/с
Некогернтный	0.0444	0.041	0.042	1.06·106бит/с

Как видно из таблицы 2 при когерентном приеме сигнала вероятности