Разработка системы связи для передачи дискретных сообщений. Канальное кодирование кодом Хемминга. Схема системы связи для передачи дискретных сообщений

работе используется бинарный код, то максимальная энтропия равна 1 бит

Н_max=1 бит

c(B)=(1-0.991)/1

c(B)=8,866×10^-3

Скорость передачи информации рассчитаем по формуле (5.10)

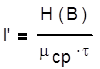
(5.10)

I¢=0.091/(3,693×1,2×10^-6)

I¢=2.237×10⁵ (бит/сек)

6. Описание процесса принятия приемником решения при приеме сигнала.

На первый взгляд принцип оценки качества приема вероятностью правильного приема символа кажется вполне естественным и даже единственно возможным. Ниже будет показано, что это не всегда так и что существуют и другие критерии качества, применимые в тех или иных частных случаях.

Пусть при передаче дискретных сообщений используются реализации сигнала S_i(t), соответствующие кодовым символам. В течение интервала времени от 0 до Т на вход приемного устройства поступает некоторое колебание, которое вследствие искажений и помех (x(t)) в канале не совпадает в точности ни с одним из передаваемых сигналов. Следовательно, в этом случае приемное устройство должно выбрать одну из n возможных взаимоисключающих гипотез. Решение о том, какой символ был передан на входе, принимается в демодуляторе. В случае, когда код бинарный демодулятор решает: был сигнал на входе или его не было («1» и «0» соответственно).

Для выполнения данной задачи устанавливается порог: если сигнал превышает заданный порог, то принимается решение в пользу «1», если – нет, то – «0».

Для того, чтобы вероятность ошибки была как можно меньше, необходимо установить оптимальный порог. При передаче дискретных сообщений в качестве критерия обычно принимают среднюю вероятность ошибки приёма одного элемента двоичной последовательности. Этот критерий называется критерием идеального наблюдателя. Он является частным случаем критерия минимума среднего риска Байеса при одинаковых штрафах за все неправильные решения. Алгоритм принятия решения отражен в формуле (6.1).

P₀×W₀(y)      p₁×W₁(y)

Данное соотношение можно переписать в виде:

     

7. Расчет характеристик системы согласно п.2.3.

Рассмотрим случай когерентного приема (прием, при котором известны параметры системы. Основная задача заключается в определении наличия сигнала):

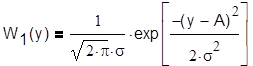Плотность распределения огибающей сигнала с шумом равна:

, а плотность распределения огибающей шума равна:

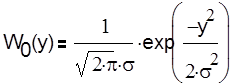
Пороговое значение определяем из равенства (7.1)

(7.1)

Z₀=3.093 (В)

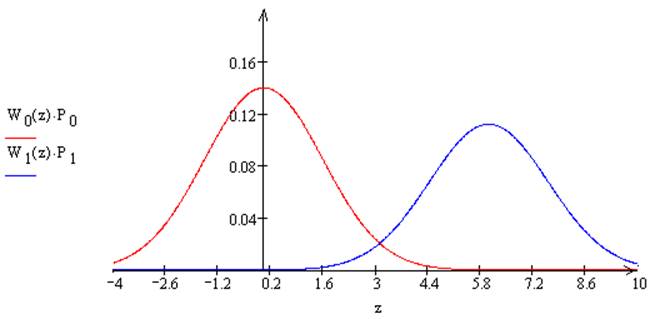Графики распределения плотностей вероятности выглядят следующим образом:

Рис. 7.1. Распределение плотности вероятности в случае когерентного приема.

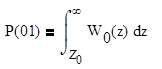    Ошибка первого рода - «ложная тревога» (передавалась единица, а принят - ноль) вычисляется по формуле (7.2).

(7.2)

    Ошибка второго рода – «пропуск» (передавался ноль, а принята единица) вычисляется по формуле (7.3).

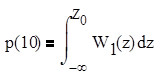(7.3)

p(0|1)=0,014

p(1|0)=0,015

    Вероятность ошибки вычисляется по формуле (7.4).

(7.4)

р_ош=0,555×0,014+0,445×0,015

р_ош=0,014

Найдем скорость передачи информации в канале с шумом:

Условные вероятности равны:

р(0|0)=1 - р(0|1)

р(1|1)=1 - р(1|0)

р(0|0)=0,976

р(1|1)=0,967

Совместные плотности вероятностей вычислим по формулам:

                                                         p(0,0)= р(0|0)×p₀=0.548                                                 (7.5)

                                                      p(0,1)= р(0|1)×p₀=6.519×10^-3                                              (7.6)

                                                      p(1,0)= р(1|0)×p₁=7.783×10^-3                                               (7.7)

                                                          p(1,1)= р(1|1)×p₁=0.548                                                   (7.8)

Среднее количество информации, теряемое при передаче произвольного сигнала по каналу с помехами находится по формуле (7.5)

Н(А/В)=р(0,0)·logр(0|0)+ р(0,1)·logр(0|1)+ р(1,0)·logр(1|0)+ р(1,1)·logр(1|1)                      (7.9)

Н(А/В)=0,108 (бит)

Тогда скорость передачи информации (R) при наличии помех в канале равна:

R=1.993·10⁵ (бит/сек)

Рассмотрим некогерентный прием:

Прием, при котором не известна начальная фаза.

    В данном случае плотность распределения огибающей суммы сигнала и шума равна:

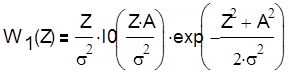Плотность распределения огибающей шума:

    Пороговое значение находится аналогично случаю когерентного приема. Используя формулу (7.1), рассчитаем Zo:

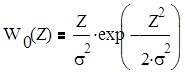Zo=3.938 (B)

 

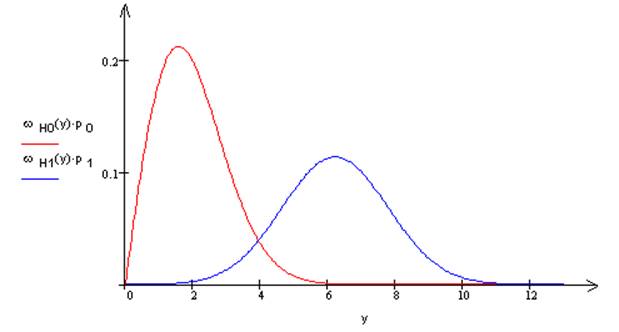
Рис. 7.2. Распределение плотности вероятности при некогерентном приеме.

Ошибки первого и второго рода найдем по формулам (7.2) и (7.3) соответственно.

p(0|1)=0.032

p(1|0)=0.025

Используя формулу (7.4) найдем вероятность ошибки:

Р_ош=0,028

Условные вероятности p(0|0) и p(1|1) равны:

p(0|0)=0,975

p(1|1)=0,968

Используя формулы (7.5)-(7.8) найдем совместные вероятности ошибок в случае некогерентного приема.

p(0,0)=0.541

p(0,1)=0.014

p(1,0)=0.014

p(1,1)=0.413

Воспользовавшись формулами (7.9) и (7.10) найдем среднее количество информации и скорость передачи информации при наличии помех в канале в случае некогерентного приема:

Н(А/В)=0,183 (бит)

R=1,822·10⁵ (бит/сек)

Сравнив полученные результаты, получим, что вероятности ошибок первого