Разработка системы связи для передачи дискретных сообщений. Структурная схема системы связи. Качественные временные диаграммы

Этот критерий называется критерием Байеса, а приёмник соответствующий этому критерию – Байесовским приёмником. Это наилучший критерий, потому что он учитывает все вероятности и потери.

В некоторых случаях (например, при приёме дискретных сообщений) можно назначить постоянные D_ij , тогда можно вынести  D_ij за скобку и добиваться минимума того, что осталось. В этом случае возникает средняя вероятность ошибки

N      N

р_ош = å  å р_i × р_ij .

i=0   j=0    

i¹j

Этот критерий называется критерием Котельникова (идеального наблюдателя) – критерий минимума средней вероятности ошибки. Если демодулятор удовлетворяет минимуму р_ош , то это идеальный приёмник, который принимает решение по одному отсчёту смеси сигнала с шумом Z(t₀) = S_i(t₀) + x(t₀).

Для бинарного случая средняя вероятность ошибки с учётом априорных вероятностей передачи символов р_ош = р₀ × р₀₁ + р₁× р₁₀

Вероятность ошибки зависит от: вида модуляции, способа детектирования (когерентный, некогерентный), способа фильтрации (оптимальный фильтр, не оптимальный фильтр), мощность Р_с (энергии Е_с) сигнала, мощности Р_п (спектральной плотности мощности N_п) помехи. 

Итак, имеются две гипотезы (предположения): Н₀ – передан символ 0, и Н₁ – передан символ 1. Задача проверки гипотез – это задача выбора реакции приёмника на переданные сигналы. Так как сигналы случайны, то каждой гипотезе соответствует класс ПРВ мгновенных значений. Пусть распределение вероятностей задаётся по нормальному закону, тогда для гипотез  Н₀ и Н₁ , соответственно, функции ПРВ мгновенных значений сигнала вычисляются по формулам:

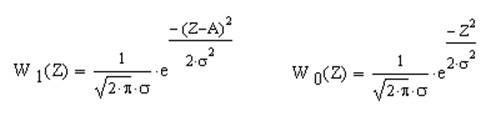
, где Z – это мгновенные значения сигнала на входе приёмника, р₀ и р₁- вероятности правильного приёма символов 0 и 1 для соответствующих гипотез.

Так как А - амплитуда и s² - дисперсия известны, то Н₀ и Н₁ – простые гипотезы и каждой из них соответствует одна ПРВ.

Принятие решения для бинарного случая согласно критерию Байеса осуществляется по следующему алгоритму:                             

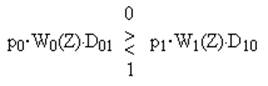
, то есть приёмник принимает решение о передаче символа “0”, если значение левой части неравенства больше значения правой, и наоборот.

Принятие решения для бинарного случая согласно критерию идеального наблюдателя (когда мы задаёмся равными потерями) осуществляется по следующему алгоритму:                             

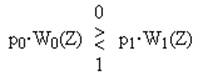
Следует отметить, что при передаче дискретных сообщений широко используется критерий Котельникова (критерий идеального наблюдателя). Согласно этому критерию принимается решение, что передан сигнал S₁(t), соответствующий передаче символа “1”, если мгновенное значение напряжения сигнала Z(t) на входе приёмника больше порогового. Аналогично, принимается решение, что передан сигнал S₀(t), соответствующий передаче символа “0”, если мгновенное значение напряжения сигнала Z(t) на входе приёмника меньше порогового.

Оптимальный порог (z_p) определяется точкой пересечения графиков функций ПРВ для мгновенных значений сигнала Z на входе приёмника

При использовании такого критерия полная вероятность ошибочного решения (или средняя вероятность - р_ош) будет минимальной.

Неравенство, по которому осуществляется принятие решения согласно критерию идеального наблюдателя, можно переписать в следующем виде:

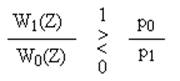
Это выражение называют отношением правдоподобия для критерия идеального наблюдателя при передаче двух сигналов. Если вероятности передаваемых символов одинаковы, то p₀ / p₁ = 1, а критерий становится общим и называется критерием максимального правдоподобия.  

Итак, для моего случая значения выражений в правой и левой частях отношения правдоподобия можно представить в численном виде.                                                                      

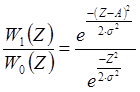
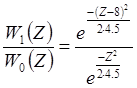
   Отношение правдоподобия примет вид: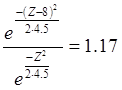     

Когерентный прием.

Вероятности ошибок первого и второго рода для когерентного приёма (когда сигналы полностью известны) рассчитываются по следующим формулам:

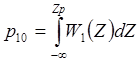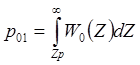, , где W₁(Z) и W₀(Z) – функции плотности распределения вероятности:  ,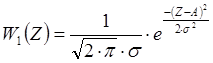 

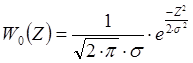
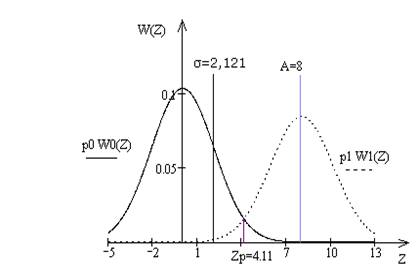Рис.6.   Графики функций ПРВ для мгновенных значений сигнала Z (когерентный прием)

Порог определяется графически, как абсцисса точки пересечения графиков ПРВ: Zp=4.11

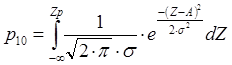
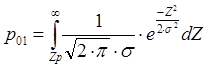
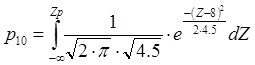
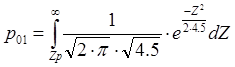
Тогда                     

С учётом вероятностей ошибок при приёме скорость передачи информации рассчитывается по следующей формуле:

   (бит/с),   где I(X,Y) – взаимная информация, вычисляемая по формуле:

         .

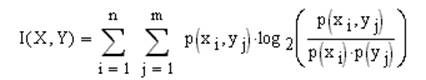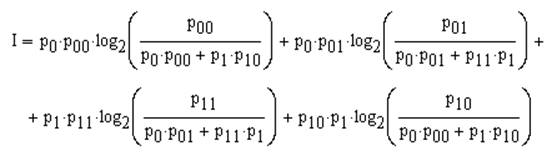
, где р₁₁ = 1 – р₁₀ и р₀₀ = 1 – р₀₁ – вероятности правильного приёма