Найти спектр сигнала в базисе Уолша, построить спектральную диаграмму.
|
|
Для этого воспользуемся данной формулой:
Waln(t) - функция Уолша n-ого порядка.
n изменяется от 0 до 7.
![]() – площадь
– площадь
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
В результате получаем спектральную диаграмму:
|
|
· Найти аналитически спектральную плотность прямоугольного видеоимпульса относительно ядра Фурье.
|
|
За прямоугольный импульс примем:
|
|
Исходя из прямого преобразования Фурье спектральная плотность данного сигнала определяется как:
S(ω)=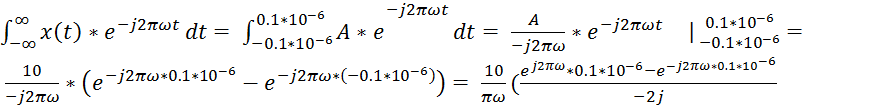 )=
)=![]()
● Найти спектральную плотность сигнала относительно ядра Фурье, построить графики её модуля и аргумента.
Решение: Для перехода описания сигнала во времени ![]() к описанию в
частотной области
к описанию в
частотной области ![]() используют прямое
преобразование Фурье:
используют прямое
преобразование Фурье:
![]()
Таким образом, одиночный импульс, заданный на всей
бесконечной оси времени, имеет сплошной спектр в виде непрерывной функции
частоты ![]() , которая называется спектральной
плотностью.
, которая называется спектральной
плотностью.
Значение спектральной плотности прямоугольного импульса находится из формулы:
![]()
Используем одну из основных теорем о спектрах – теорему о
сдвиге: ![]()
Найдём длительность и задержку исходного сигнала:
Длительность: ![]() ,
,
Задержка: ![]() .
.
Подставляем в формулу и получаем:
![]()
Откуда графики модуля и аргумента выглядят следующим образом:
|
|
|
|
● Найти спектр периодической последовательности, полученной повторением данного сигнала, относительно комплексного базиса Фурье, построить амплитудную и фазовую спектральные диаграммы.
Спектральная плотность связана простым соотношением
с амплитудами периодического сигнала ![]() ,
полученного повторением с периодом
,
полученного повторением с периодом ![]() одиночного
импульса
одиночного
импульса ![]() .
. ![]()
![]()
|
|
В нашем случае имеем следующее: ![]()
Для наглядности графики спектральных диаграмм изобразим совместно:
|
|
● Найти автокорреляционную функцию сигнала, построить график.
Решение: Одной из важных временных
характеристик детерминированных сигналов, устанавливающих энергетическую связь
сигнала ![]() с его сдвинутой на
величину
с его сдвинутой на
величину ![]() копией
копией ![]() , является автокорреляционная
функция (АКФ).
, является автокорреляционная
функция (АКФ).
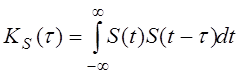
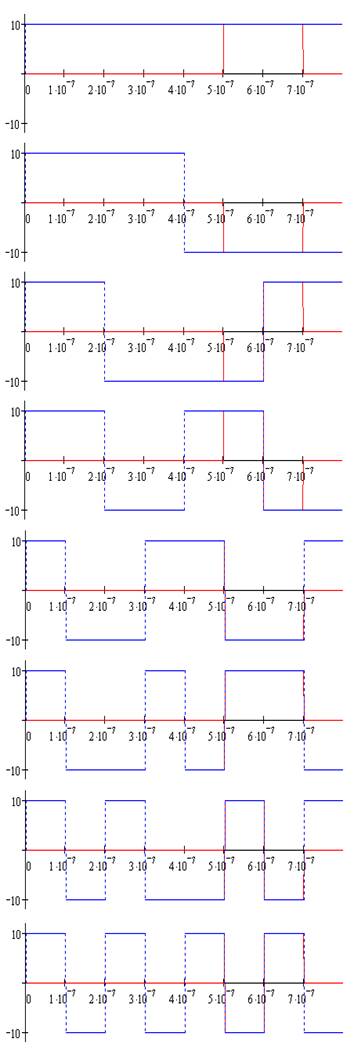
В теории сигналов также доказывается, что АКФ и энергетический спектр связаны парой преобразований Фурье:
![]()
Графически изобразим принцип метода
определения АКФ. Для этого покажем степень связи (корреляции) сигнала ![]() со своей копией,
сдвинутой на величину
со своей копией,
сдвинутой на величину ![]() по оси
времени. На графиках, приведенных ниже, можно
наблюдать смещение оригинала и копии сигнала на величину Δt (Δt = 0..8·10-7 c.).
по оси
времени. На графиках, приведенных ниже, можно
наблюдать смещение оригинала и копии сигнала на величину Δt (Δt = 0..8·10-7 c.).
Сi – интервал совпадения сдвинутого сигнала с оригиналом
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ясно, что функция ![]() достигнет своего
максимума при
достигнет своего
максимума при ![]() . При этом
максимальное значение корреляционной функции равно энергии сигнала.
. При этом
максимальное значение корреляционной функции равно энергии сигнала.
|
|
В результате получаем график:
● Определить эффективную ширину спектра.
Решение: Полная энергия одиночного импульса может быть вычислена либо во временной области, либо в частотной в соответствии с равенством Парсеваля:
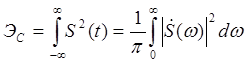
В частотной области можно определить эффективную ширину спектра сигнала ωэф - это такой частотный интервал, в котором сосредоточена подавляющая часть (kэ) полной энергии сигнала. Обычно kэ = 0.9(90%) или 0.95(95%). Она находится так:
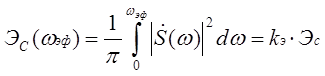
|
|
Так как автокорреляционная функция достигает максимума при τ = 0, то максимальная энергия сигнала равна:
|
|
|
|
Значит, эффективная энергия равна:
Предположим, что:
|
|
Тогда, используя блок Given-Find, определим эффективную ширину спектра сигнала:
|
|
|
|
Следовательно, ωэф=6.512·107 рад/с.
|
|
● Найти сигнал, который получается из заданного при воздействии фильтра с прямоугольной АЧХ и линейной ФЧХ (частота среза fсрфильтра в МГц и крутизна S ФЧХ в рад/МГц приведены в табл. 2), построить временной график полученного сигнала.
Таблица 2.
|
Вариант |
2 |
|
Fср |
22 |
|
Подвариант |
1 |
|
S |
0.9 |
Решение: Определим передаточную функцию цепи
имея данные значения частоты среза ![]() фильтра
и крутизны
фильтра
и крутизны ![]() :
: ![]() , где
, где ![]() вышеупомянутая
функция Хевисайда.
вышеупомянутая
функция Хевисайда.
Представим исходный сигнал в операторном виде применив прямое преобразование Лапласа:
![]() ,
,
заменив ![]() на
на ![]() получаем:
получаем:
![]() .
.
Выходной сигнал в частотной области имеет вид:
![]()
Тогда, чтобы найти сигнал во временной области воспользуемся формулой:
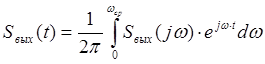 .
.
|
|
Подставляя в данный вид уравнения найденные значения, в системе MathCAD, получаем временной график полученного сигнала при воздействии фильтра:
● Найти сигнал, который получается из заданного при воздействии RС-фильтра НЧ с параметрами, указанными в табл. 3 (R в кОм, С в пФ), построить временной график полученного сигнала
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.