передачи «1» используется радиоимпульс, для передачи «0» -отсутствие радиоимпульса. Для моделирования такой системы помехи будем считатьаддитивным гауссовским белым шумом с нулевым математическим ожиданием.
 Временные диаграммы
Временные диаграммы
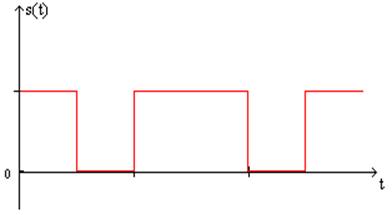
Рис.2 Сигнал на выходе кодера.
 |
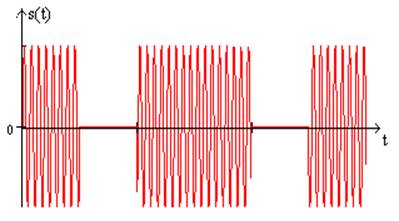
Рис.3 Сигнал на выходе модулятора.
 |
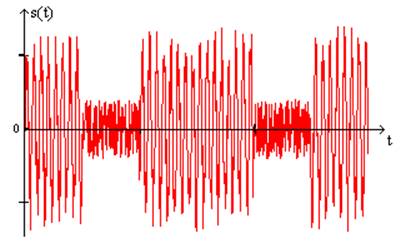
Рис.4 Сигнал с помехой на входе демодулятора.
 |
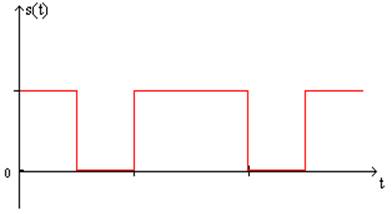
Рис.5 Сигнал на входе декодера .
|
xi |
код |
p(xi) |
μ |
|
р |
011 |
0,121 |
3 |
|
н |
100 |
0,107 |
3 |
|
а |
101 |
0,105 |
3 |
|
в |
110 |
0,105 |
3 |
|
е |
111 |
0,094 |
3 |
|
к |
0000 |
0,093 |
4 |
|
и |
0010 |
0,087 |
4 |
|
с |
0011 |
0,07 |
4 |
|
о |
0100 |
0,066 |
4 |
|
п |
00010 |
0,055 |
5 |
|
ж |
00011 |
0,036 |
5 |
|
б |
01011 |
0,025 |
5 |
|
д |
010100 |
0,02 |
6 |
|
м |
010101 |
0,016 |
6 |
Закодируем следующую фразу: новое.кодирование.неверно
Код фразы: 100.0100.110.0100.111.0000.0100.010100.0010.011.0100.110.101.100.0010.111. 100. 111.110. 111.011.100.0100.
Теорема Шеннона(в отсутствие шума): Среднее число кодовых символов, приходящееся на один
символ сообщения, можно как угодно приблизить к величине
Н / log(L) , где L –число
кодовых символов.
Если символы алфавита неравновероятны и независимы, то более вероятным символам ставятся в соответствие более короткие кодовые комбинации. Значит, для кодирования неоптимального источника нужно использовать неравномерный код. Для неравномерных кодов непременно должно выполняться префиксное условие: код должен быть неперекрываемым, т.е. никакая кодовая комбинация не является началом другой кодовой комбинации.
Производительность источника: Н'=Н/τ [бит/с], τ - время передачи одного символа
Скорость передачи информации:I’xy=Ixy/τ [бит/с], где Ixy - количество информации, пере-
данной от X к Y
Пропускная способность канала: С=max I’xy
Теорема Шеннона (для канала с помехами):Если производительность источника Н' меньше пропускной способности канала С, то существует процедура кодирование-декодирование, при которой вероятность ошибочного декодирования сколь угодно мала.
Если Н'![]() С, то для
уменьшения вероятности появления ошибки кодовые комбинации нужно делать
большими, но это влечет за собой задержку во времени, то в
противном случае ошибка неизбежна.
С, то для
уменьшения вероятности появления ошибки кодовые комбинации нужно делать
большими, но это влечет за собой задержку во времени, то в
противном случае ошибка неизбежна.
Расчет энтропии и избыточности источника:
μср=![]() pi×μi , где μср
- средняя
длина кодовой комбинации, μi - длина i буквы;
pi×μi , где μср
- средняя
длина кодовой комбинации, μi - длина i буквы;
μср= ![]()
Н =![]() - энтропия источника;
- энтропия источника;
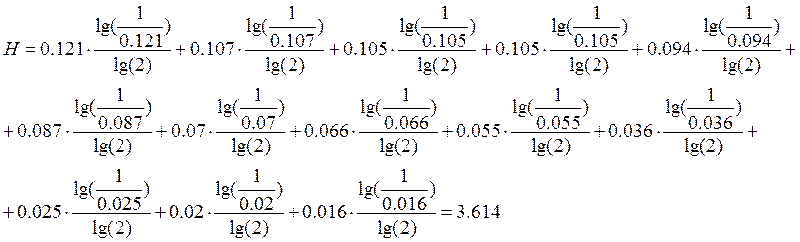
Hmax =![]() , где n – количество букв алфавита;
, где n – количество букв алфавита;
Hmax = 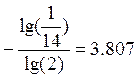
c = (Hmax-H)/Hmax ![]() ; избыточность источника;
; избыточность источника;
![]() производительность
источника;
производительность
источника; ![]()
Расчет вероятностей передаваемых символов, избыточности кода, скорости передачи информации:
Вероятность символа
«0»: ![]() , где
, где ![]() -
количество нолей в i-ой кодовой строке;
-
количество нолей в i-ой кодовой строке;
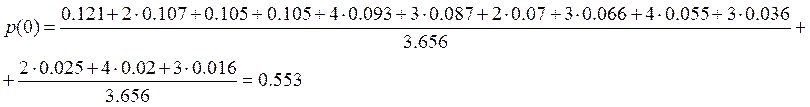
Вероятности p(0) и p(1) связаны соотношением: p(0)+ p(1)=1,получаем p(1) = 1- p(0);
![]()
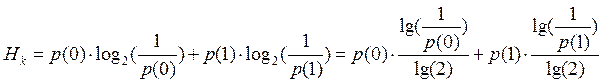 ;
;
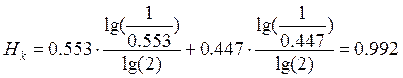
При передаче бинарного кода: Нк мах=1.
Избыточность кода: 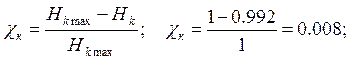
Скорость передачи
информации: ![]()
Процесс принятия приемником решения при приеме сигнала.
В системах передачи информации с пассивной паузой, использующих бинарный код (совокупность «0» и «1») решающее устройство должно однозначно определять есть сигнал в линии связи или нет, т.е. передавался символ «0» или «1».Задача демодулятора по наблюдаемому канальному сигналу z(t)принять решение о переданном сигнале. Закон преобразования z(t) > b’ц(t) называется правилом решения алгоритмом работы демодулятора.
Если поступивший из линии сигнал превышает установленный пороговый уровень передана «1», ниже порогового уровня-«0».Этот алгоритм легко реализуется в современной электронике с помощью микросхем-компараторов, сравнивающих два сигнала, один из которых поступает из линии, а другой является эталонным, он и играет роль порога.
Вот только какой величины этот порог устанавливать? Если не большой, то демодулятор будет обнаруживать каждый переданный импульс, даже c сильно искаженный помехами, но из-за частого превышения шумом невысокого порога за «1» будут приняты переданные «0».Если порог сделать очень высоким, демодулятор не будет пропускать переданные «0», но некоторые импульсы, означающие передачу «1», будут восприняты за «0».
Критерий идеального наблюдателя(Критерий Котельникова).
Самым лучшим приемником является оптимальный по критерию Байеса, но при его расчете появляется трудность - оценка потерь. Если принять потери за ошибочные решения одинаковыми, то от критерия Байеса мы перейдем к критерию идеального наблюдателя, который сводится к отысканию минимума средней вероятности ошибки.
Гипотеза Н0: передан символ «0»
Гипотеза Н1: передан символ «1»
Рош=Р0*Р01+Р1*Р10
Когерентный прием.
Плотности распределения вероятностей мгновенных значений колебания на входе демодулятора при приеме посылки и паузы:
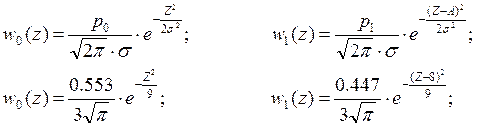
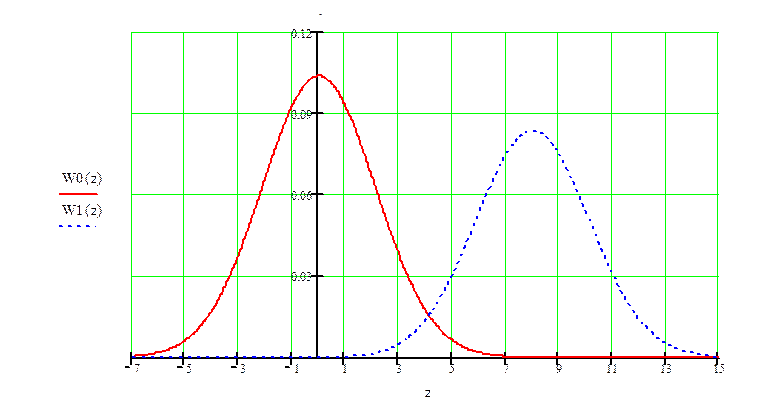
По графику определяем ![]() , так как
, так как ![]()
Теперь определяем вероятность
ошибки первого рода (ложной тревоги) ![]() и
вероятность ошибки второго рода (пропуск сигнала)
и
вероятность ошибки второго рода (пропуск сигнала) ![]() , где
, где
 ;
;

Найдем среднюю вероятность ошибки ![]() ;
;
![]() ;
;
![]() так
как
так
как ![]() , то
, то ![]()
p01 – вероятность «1» при передачи «0»
p10 – вероятность «0» при передачи «1»
Найдем скорость передачи информации при наличии помех:
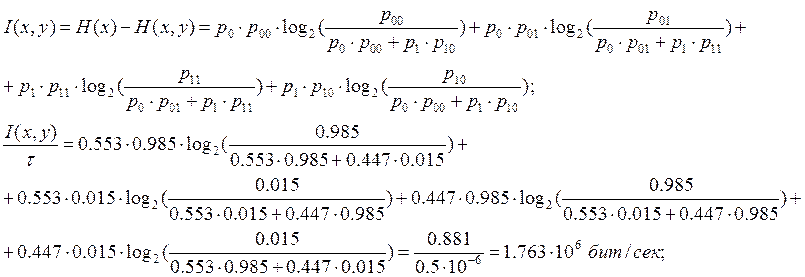
Некогерентный прием.
Запишем плотность распределения огибающей помехи и плотность распределения огибающей суммы сигнала и помехи, которые определяются законом и обобщенным законом Рэлея.
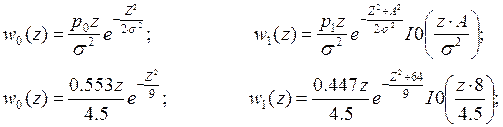
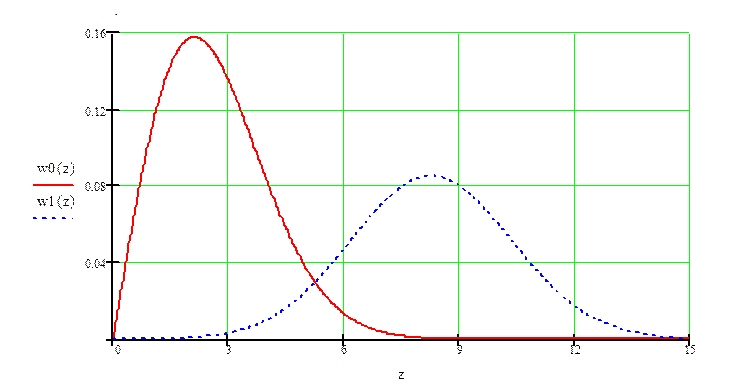
По графику определяем ![]() , так как
, так как ![]()
Теперь определяем вероятность
ошибки первого рода (ложной тревоги) ![]() и
вероятность ошибки второго рода (пропуск сигнала)
и
вероятность ошибки второго рода (пропуск сигнала) ![]() , где
, где
 ;
;
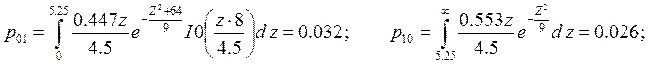
Найдем среднюю вероятность ошибки ![]() ;
;
![]() ;
;
![]()
![]()
Найдем скорость передачи информации при наличии помех:
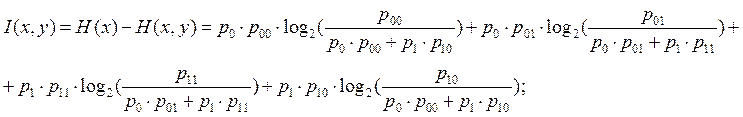
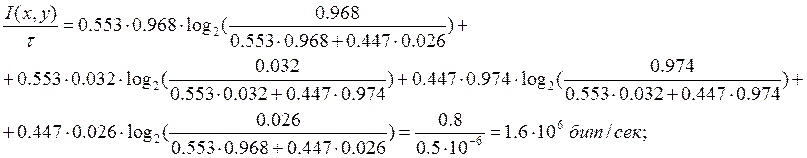
Ниже в таблице приведены сравнения вероятности ошибок первого и второго рода, средних ошибок, при когерентном и некогерентном приеме:
|
|
|
|
|
|
когерентный |
0,015 |
0,015 |
0,015 |
|
некогерентный |
0,032 |
0,026 |
0,029 |
Из данной таблицы видно, что вероятности ошибок первого и второго рода
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.