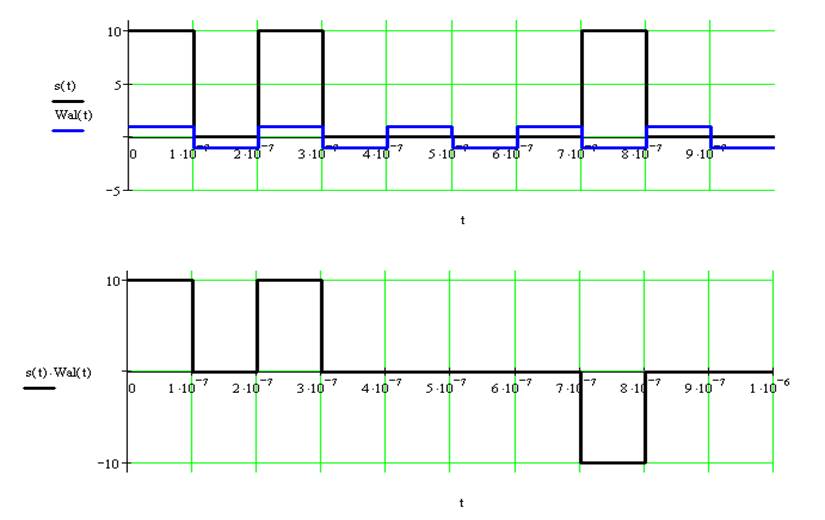
Записать математическую модель сигнала в виде линейной комбинации функций Хевисайда, построить временной график
![]() -
амплитудное значение сигнала,
-
амплитудное значение сигнала,
![]() -
продолжительность одного импульса,
-
продолжительность одного импульса,
![]() - функция
Хевисайда
- функция
Хевисайда
![]()
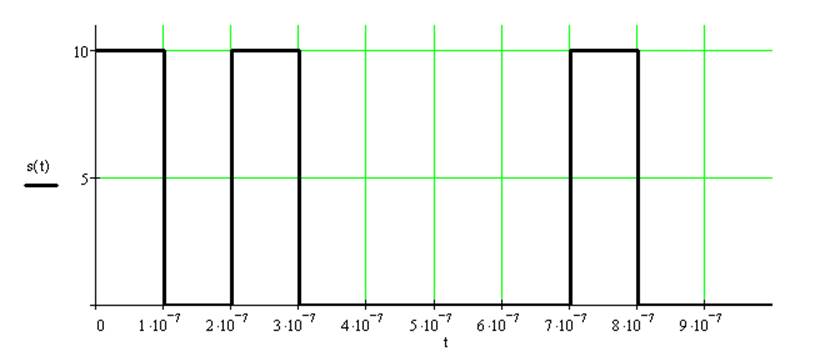
Найти спектр сигнала в базисе Уолша, построить спектральную диаграмму
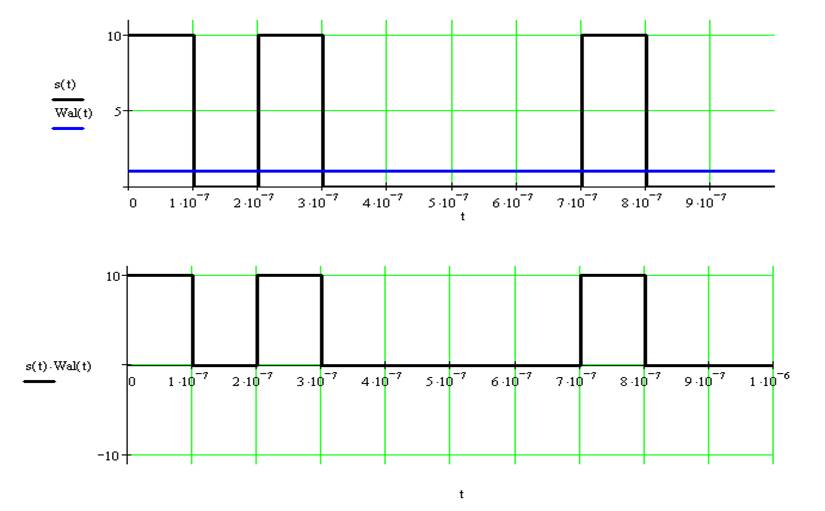
В данном РГЗ имеет смысл рассматривать только 8
первых функций Уолша.
первая функция Уолша ![]()
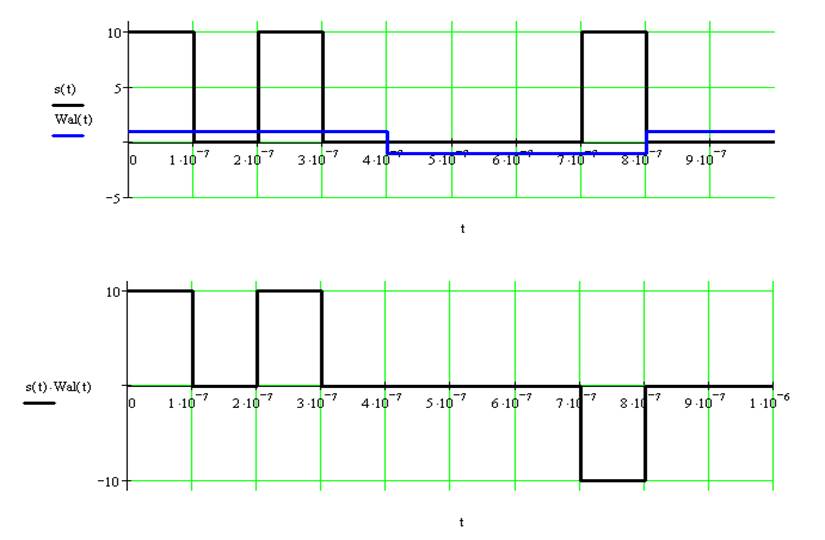
вторая функция Уолша ![]()
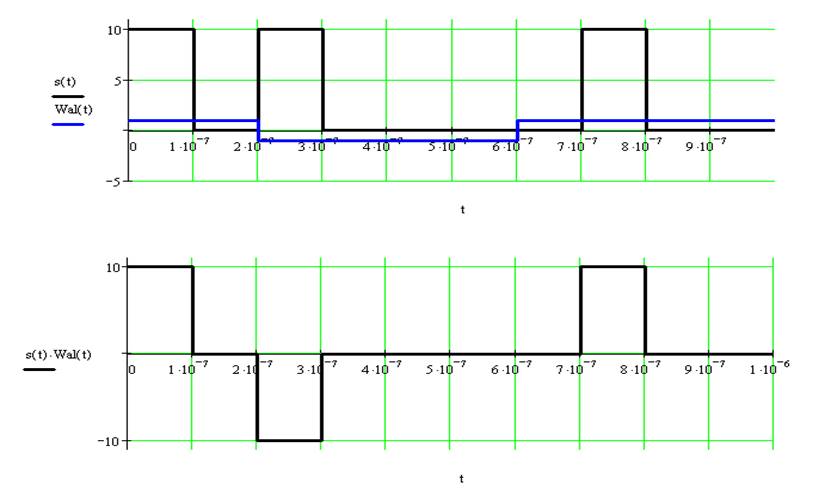
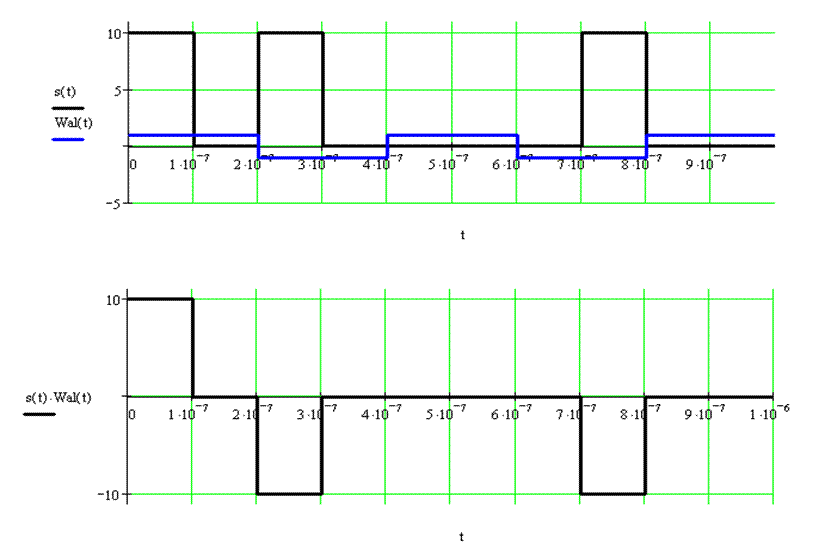
третья функция Уолша ![]()
четвертая функция Уолша ![]()
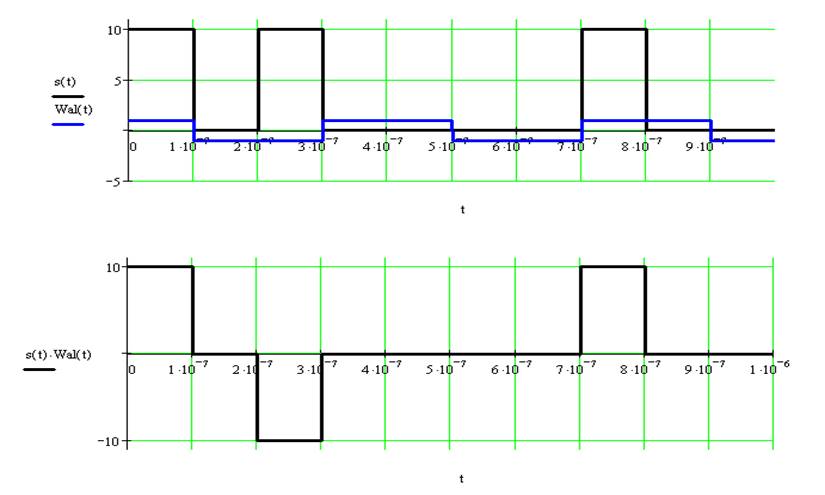
пятая функция Уолша ![]()
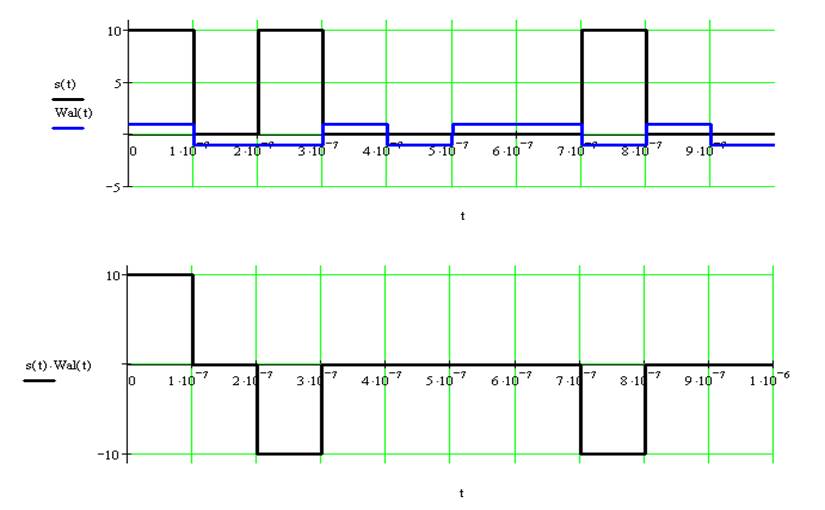
шестая функция Уолша ![]()
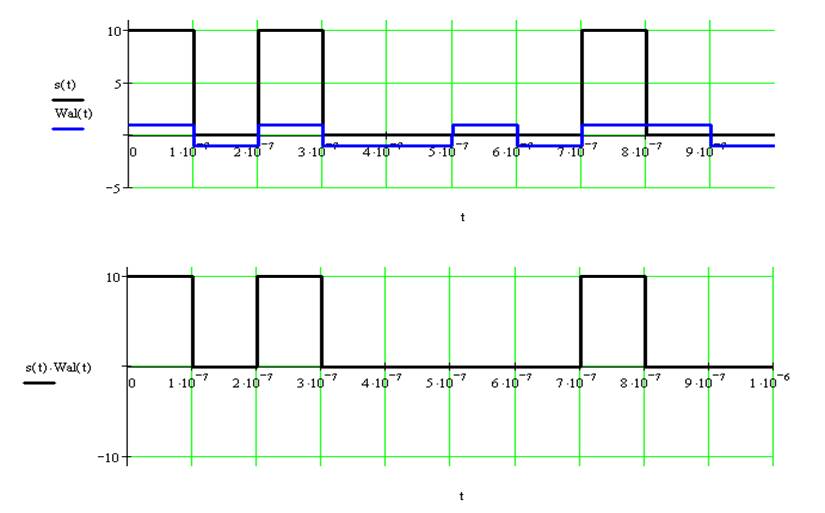
седьмая функция Уолша ![]()
 |
восьмая функция Уолша ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
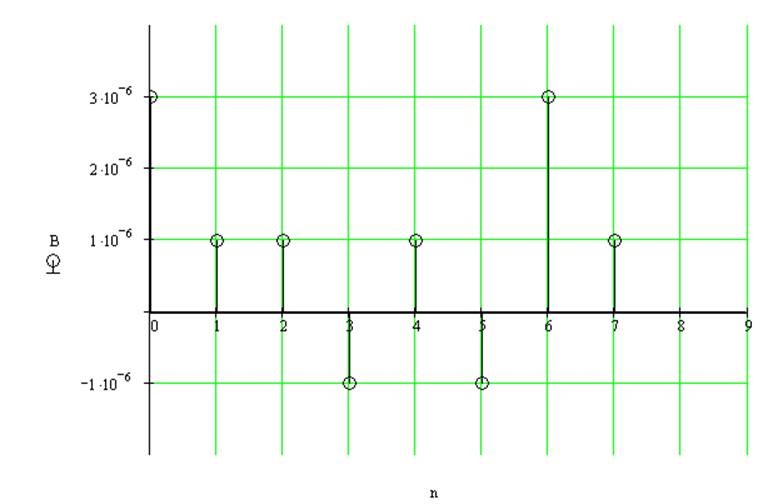
Следовательно, спектр сигнала в базисе Уолша выглядит следующим образом:
 |
Нахождение спектральной плотности сигнала относительно ядра Фурье, построение графиков ее модуля и аргумента.
![]()
Модуль спектральной плотности:
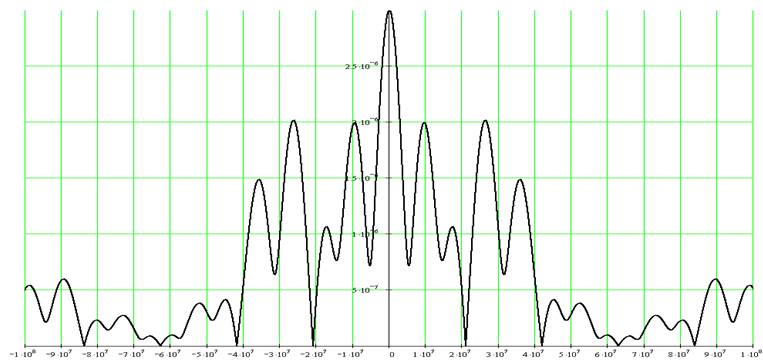
Аргумент спектральной плотности:
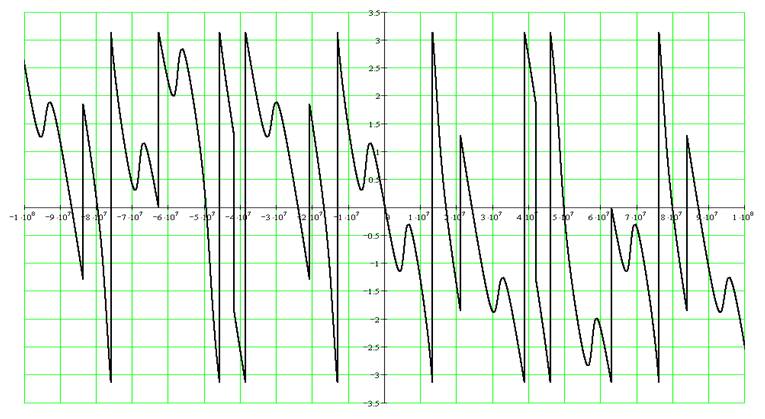
Нахождение спектра периодической последовательности, полученной повторением данного сигнала, относительно комплексного базиса Фурье, построение амплитудной и фазовой спектральные диаграммы.
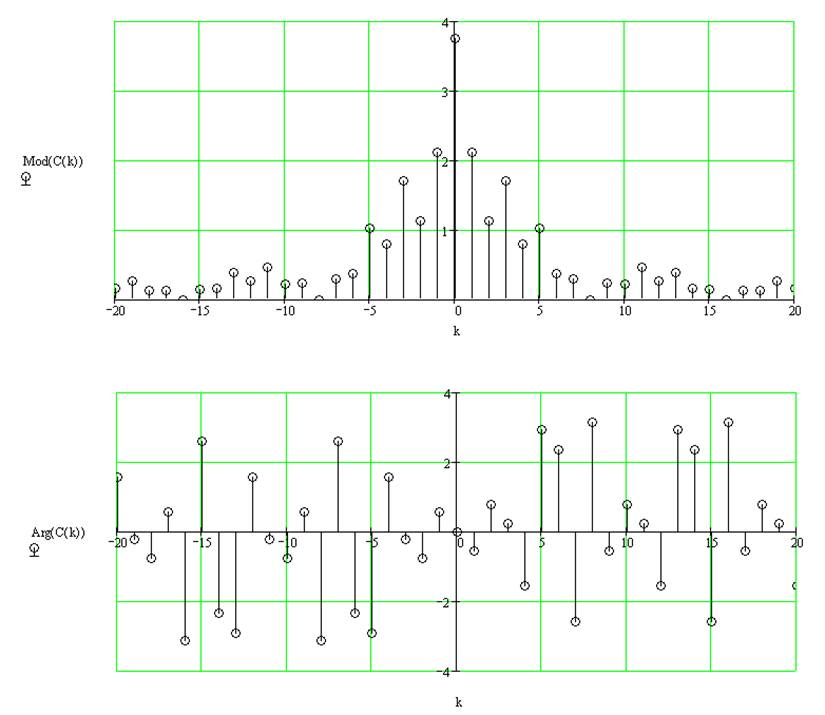
Нахождение автокорреляционной функции сигнала, построение ее графика
График автокорреляционной функции заданного сигнала имеет следующий вид:
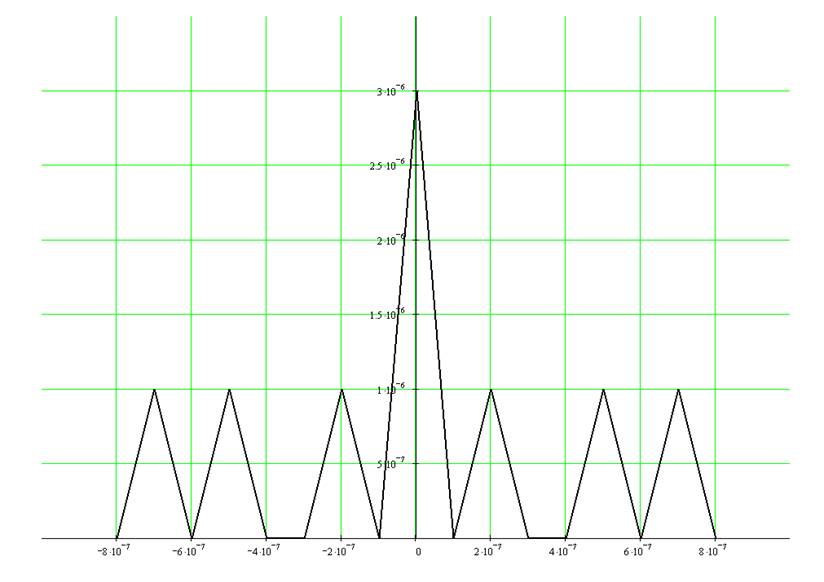
Определение эффективной ширины спектра.
Эффективная ширина спектра – это диапазон частот, внутри которого сосредоточено 95% энергии сигнала, то есть:
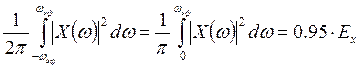
Значение частоты – границы эффективной ширины спектра:
![]()
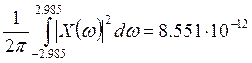
![]() .
.
На
интервале от ![]() до
до ![]() сосредоточено
95% энергии сигнала
сосредоточено
95% энергии сигнала
Нахождение сигнала, который получается из заданного, при воздействии фильтра с прямоугольной АЧХ и линейной ФЧХ, построение временного графика полученного сигнала
fср=22 МГц, S=0,65 рад/МГц
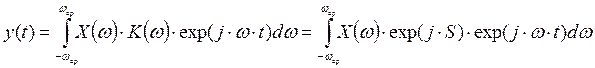
Для данного случая имеем:
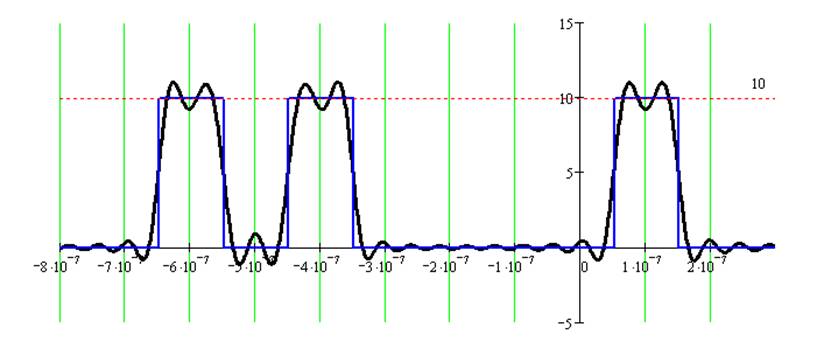
Нахождение сигнала, который получается из заданного при воздействии RC-фильтра НЧ, построить временной график полученного сигнала
R=0.28 кОм, C=650 пФ
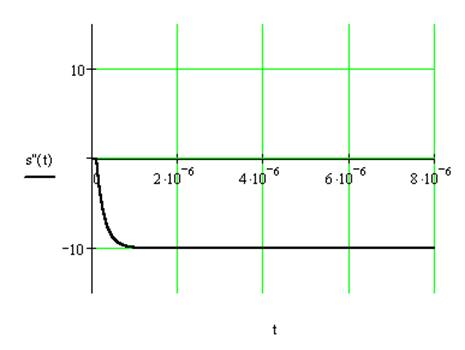
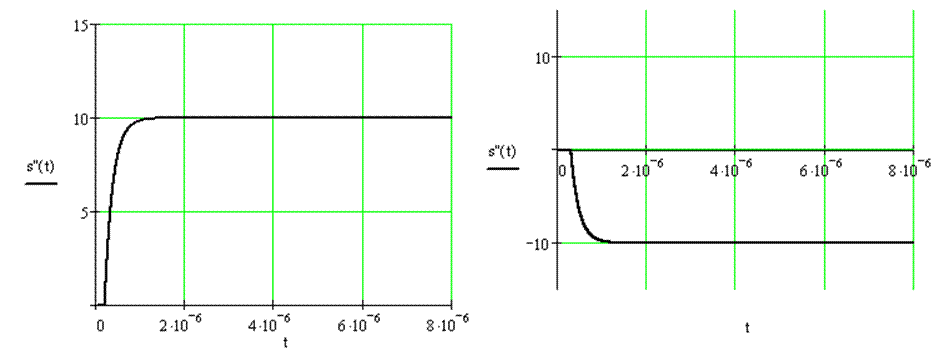
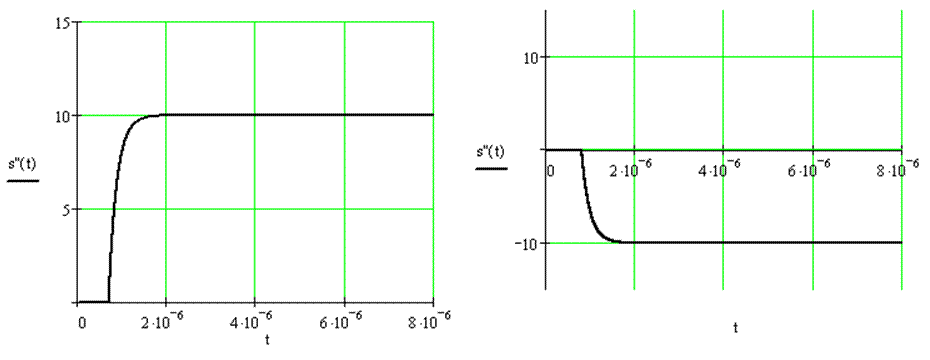
Импульсная характеристика фильтра НЧ имеет следующий вид:
![]() , где
, где ![]() ,
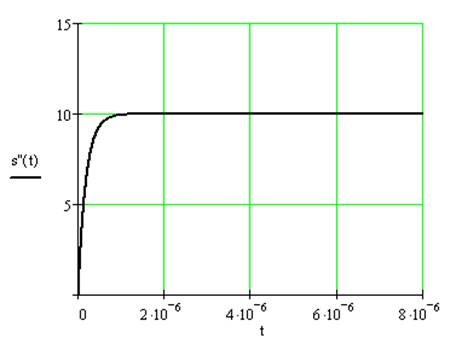
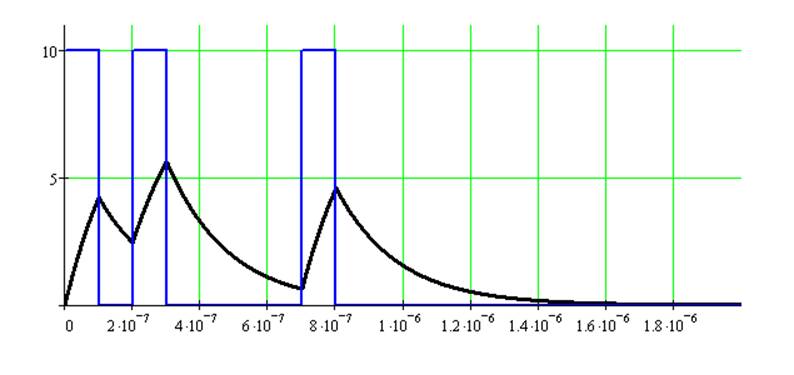
следовательно, сигнал на выходе можно представить как суммы сигналов –
воздействий отдельных функций Хевисайда:
,
следовательно, сигнал на выходе можно представить как суммы сигналов –
воздействий отдельных функций Хевисайда:
 |
|||
 |
|||
![]()
![]()
![]()
![]()
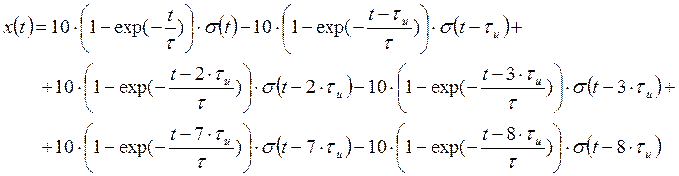 |
 |
Линейные инвариантные к сдвигу цепи.
Нахождение комплексной частотной характеристики цепи.
Построение графиков АЧХ и ФЧХ.
Согласно варианту РГЗ, задана следующая ЛИС-цепь:
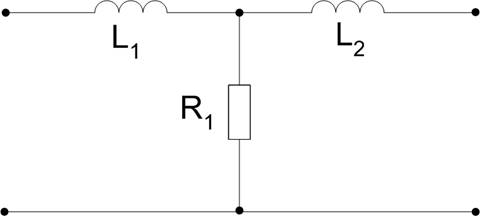 |
с параметрами:
![]()
![]()
![]()
Для удобства преобразуем Т-образную схему в П-образную:
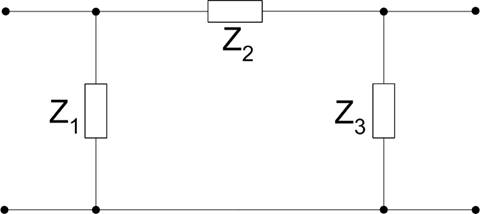 |
для данной схемы значения сопротивлений:
![]()
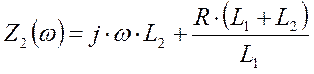
![]()
Тогда комплексная частотная
характеристика ![]() для данной схемы:
для данной схемы:
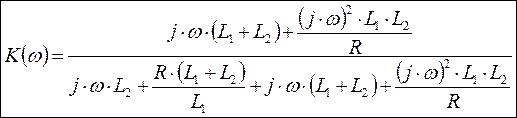 |
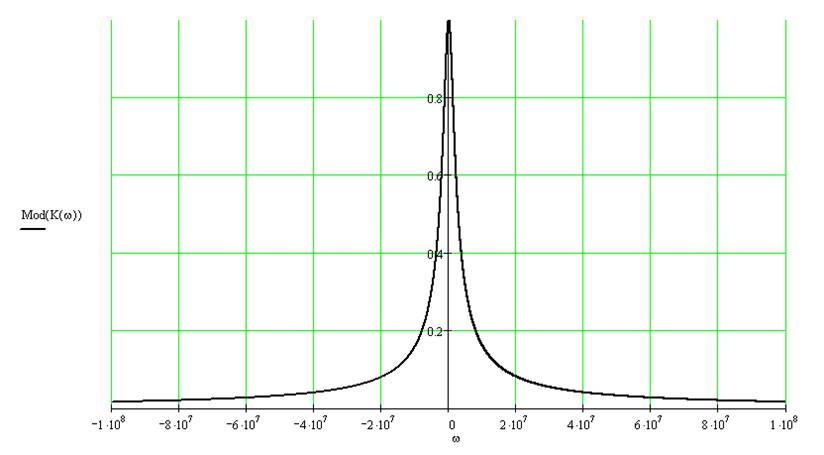
Модуль комплексной частотной характеристики для
цепей есть АЧХ:
Аргумент комплексной частотной характеристики для цепей есть АЧХ:
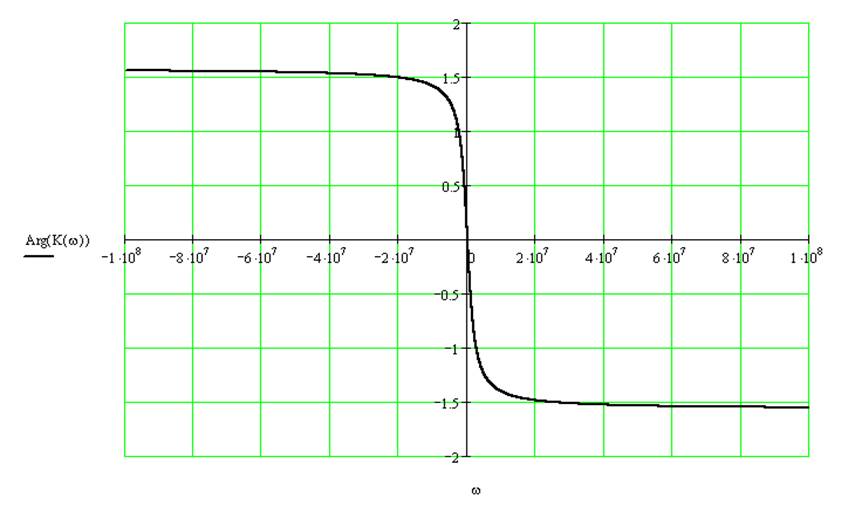
Нахождение импульсной и переходной характеристик
Для простоты нахождения импульсной характеристики воспользуемся операторным методом:
произведем
замену ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Функция ![]() аналитична на всей плоскости p за
исключением конечного числа точек p1, p2, … pn,
являющихся корнями знаменателя. Данные точки, то есть корни уравнения, называют
полюсами передаточной функции K(p). В нашем случае возможны два полюса:
аналитична на всей плоскости p за
исключением конечного числа точек p1, p2, … pn,
являющихся корнями знаменателя. Данные точки, то есть корни уравнения, называют
полюсами передаточной функции K(p). В нашем случае возможны два полюса:
![]()
![]()
Переходная характеристика цепи вычисляется по формуле:
![]()
Импульсная характеристика цепи вычисляется по формуле:
![]()
В
этих формулах ![]() - функция Хевисайда.
- функция Хевисайда.
Для нашего конкретного примера переходная и импульсная характеристики примут следующий вид:
![]()
![]()
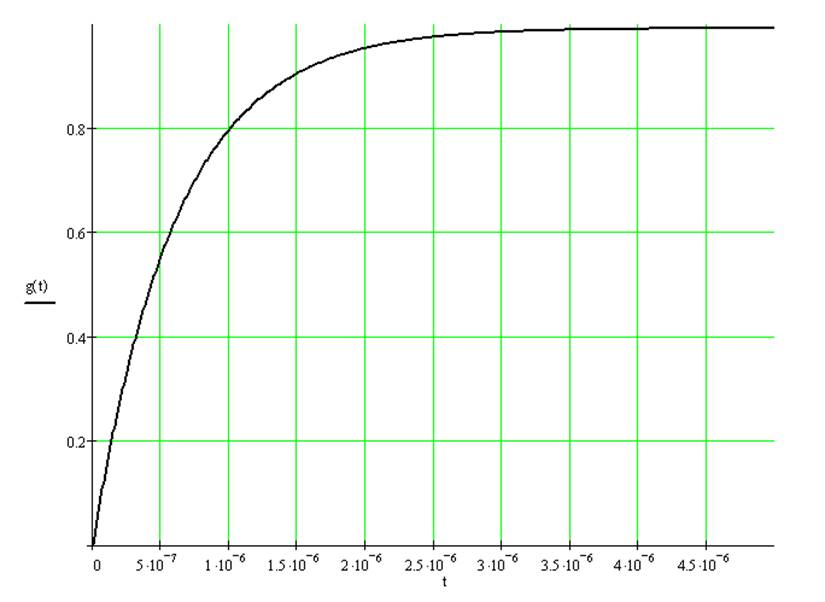
Переходная характеристика:
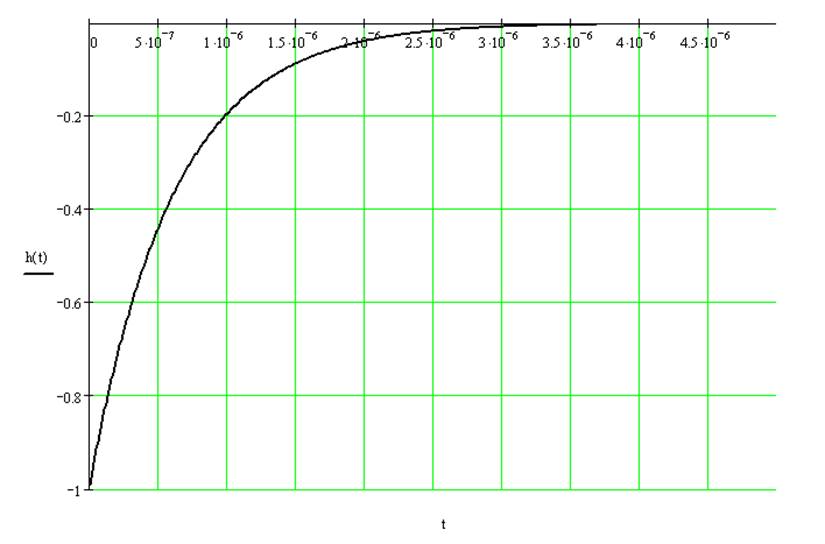
Импульсная характеристика:
Нахождение отклика цепи на заданный сигнал.
Отклик на воздействие, как и ранее, найдем как сумму откликов на одиночные функции Хевисайда:
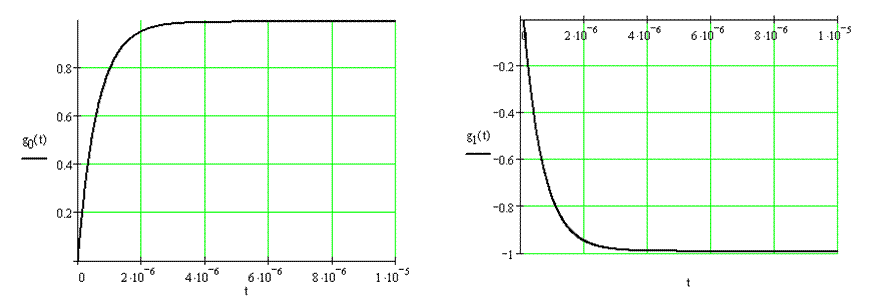
![]()
![]()
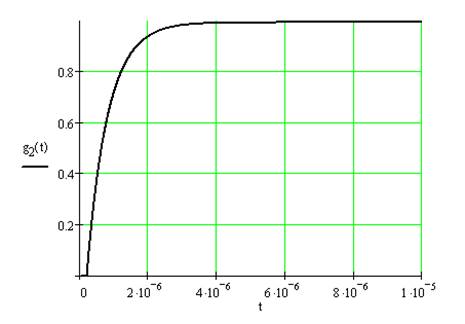
![]()
![]()
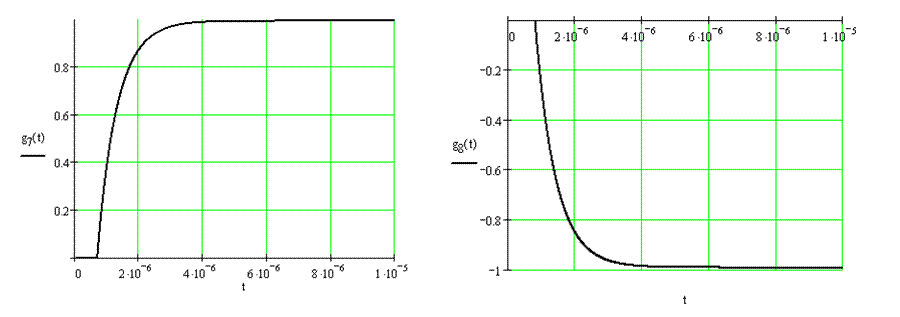
![]()
![]()
отклик цепи на заданный сигнал имеет следующий вид:
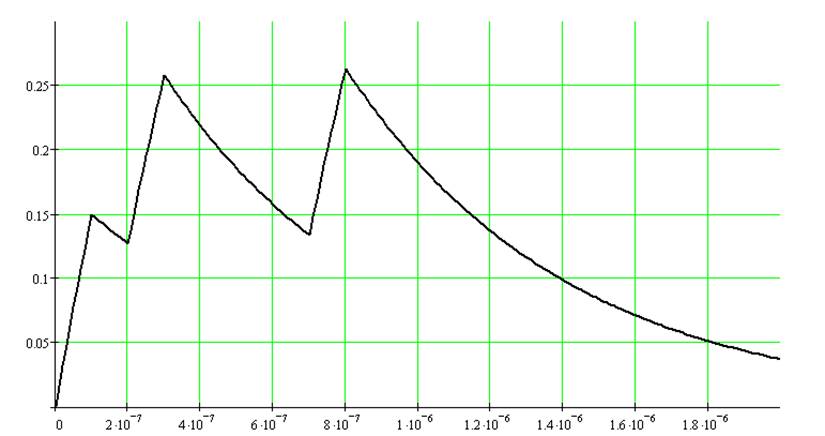 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.