











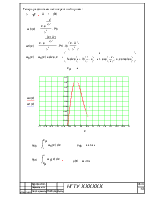





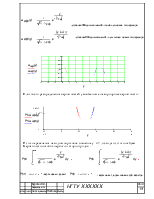







кодере источника каждый символ преобразуется в кодовую
комбинацию- совокупность «0» и «1» Рис.2.
В системе передачи с пассивной паузой «1» соответствует высокий
уровень напряжения, «0»- низкий.
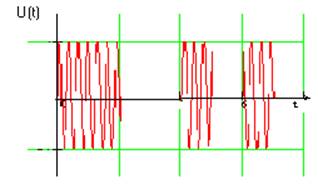
Рис.3.Сигнал на выходе Модулятора.
В модуляторе сигнал высокого уровня напряжения преобразуется в
радиоимпульс U(t) Рис.3.
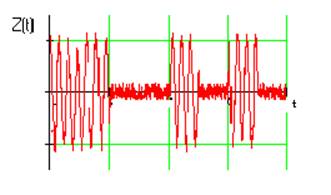
Рис.4.Сигнал на входе Демодулятора.
При прохождении сигнала по каналу связи к нему добавляется
аддитивная помеха n(t) Рис.4.
Изм. Лист
НГТУ XXXXXX
5
Nо документа
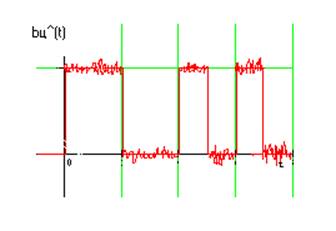
Рис.5.Сигнал на выходе Демодулятора.
В демодуляторе восстанавливаются переданные видеоимпульсы
искаженные из-за действия помех Рис.5, т.е. принимается решение,
какой сигнал пришел из линии, «0» или «1»-происходит различение
сигналов.
Декодер источника преобразует комбинации «0» и «1» в сообщение,
близкое к передаваемому источником (искаженное из-за действия
помех): с, у, и, м, …
Кодирование источника уменьшает нагрузку на канал связи.
Кодирование источника – это представление символов источника
Словами неравномерного кода с целью более полного использования
канала связи Другое название кодирования источника - сжатие. Оно
происходит без потерь информации. Числовой характеристикой
источника информации является энтропия источника. Если все
поступающие от источника символы равновероятны, то такой источник
имеет максимальную энтропию, т.е. максимально информативен.
Избыточность источника рассчитывается по такой формуле:
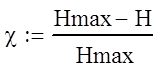
Н-это энтропия источника, а Нмах – энтропия источника который
имеет символы с равными вероятностями появления в слове Р1i:
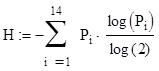
Изм. Лист
НГТУ XXXXXX
6
Nо документа
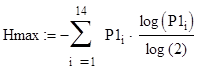
Кодовая комбинация (кодовое слово) – это последовательность
канальных символов соответствующая символам источника .
Теорема Шеннона(в отсутствие шума):
Среднюю длину кодовых слов для передачи символов источника А
с помощью кода с основанием (м) можно приблизить к величине :
Н(А)/log(m) .
Смысл экономного кодирования заключается в том чтобы сделать
вероятности канальных символов как можно более одинаковыми ,
то есть буквы имеющие наибольшую вероятность кодируются
наименьшим количеством символов.
Префиксное свойство кода : ни одна кодовая комбинация не являет-
ся началом другой . Это свойство обеспечивает мгновенное декоди-
рование . Код называется непрерываемым (неприводимым) .
Теорема Шеннона (для канала с помехами):Если производительность источника Н^(А) меньше пропускной способности канала (C), то существует по крайней мере одна процедура кодированиедекодирование, при которой вероятность ошибочного декодирования и ненадёжность (Н(А/В)) сколь угодно мала.
Если же Н^(А) больше (С) то такой процедуры не существует .
А если меньше то нужно в кодовую комбинацию вводить дополнитель
ные символы (проверочные) для повышения помехоустойчивости , но
это приводит к задержки передачи информации .
Построение кода Шеннона-Фано .
1. Все символы источника записываются в порядке убывания их веро-
ятностей .
2. Все символы делятся на две группы так чтобы суммарные вероятности групп были одинаковыми .
3. В первой группе записываются единицы во второй нули и так далее .
4. Средняя длинна
кодовой комбинации 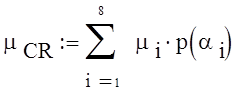
Изм. Лист
.
НГТУ XXXXXX
7
Nо документа
Символ и его
вероятность
Комбинация канальных символов
Длина кодового слова
![]()
![]()
1-ый
2-ой
3-ий
4-ый
5-ый
6-ой
![]()
р
0,122
0
0
0
---
---
---
3
н
0,107
0
0
1
---
---
---
3
а
0,105
0
1
0
---
---
---
3
в
0,105
0
1
1
0
---
---
4
е
0,094
0
1
1
1
---
---
4
к
0,093
1
0
0
---
---
---
3
и
0,087
1
0
1
0
---
---
4
с
0,07
1
0
1
1
---
---
4
о
0,066
1
1
0
0
---
---
4
п
0,055
1
1
0
1
---
---
4
ж
0,036
1
1
1
0
0
---
5
б
0,025
1
1
1
0
1
---
5
д
0,02
1
1
1
1
0
---
5
м
0,016
1
1
1
1
1
---
5
Теперь закодируем произвольную фразу построенным кодом :
Фраза : Деревонавекидома
Код :
11110.0111.000.0111.0110.1100.001.010.0110.0111.100.1010.11110.1100.11111.010
Средняя длинна кодовой
комбинации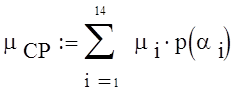
![]()
Действительно, префиксное свойство выполняется. Декодирование однозначно.
Расчет энтропии и избыточности источника:
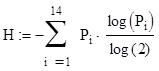
![]()
Максимальная энтропия равна :
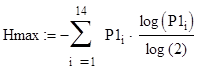
![]()
Изм. Лист
НГТУ XXXXXX
8
Nо документа
Избыточность источника равна :
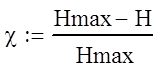
![]()
Расчет энтропии и избыточности кода, вероятности двоичных симво
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.