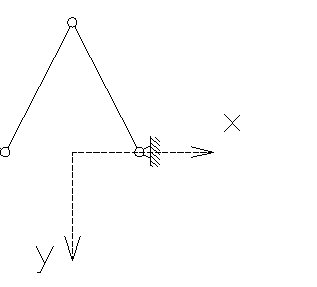
Ферма Мизеса - введение:
Следствия:
Ø большие перемещения
Ø симметричная картина деформации и несимметричная система деформации
Порядок выполнения работы.
Часть 1.1. Фиксирование положения равновесия.
Фиксируются 5 положений равновесия
Исходные данные:
Координаты точек (x;y):
т.1 (0;-12)
т.2 (0;0)
т.3 (0;12)
т.4 (4;0)
т.5 (-4;0)
l0 = 12,65.
EF = 1000.
Отсутствие нагрузки и возмущения.
Положение 1. Максимальное смещение по оси у = -12. Движение отсутствует.
Положение 2. Движение отсутствует.
Положение 3. Движение отсутствует.
Положение 4. Движение отсутствует.
Положение 5. Движение отсутствует.
Вывод: При отсутствии нагрузки и возмущения в положении равновесия движения нет.
Часть 1.2. Проверка устойчивости положения равновесия.
Придание системе начального смещения.
1.1. Симметричное смещение – вверх (у=-13).
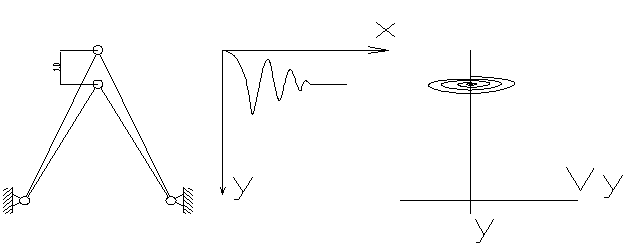 Фазовая
диаграмма.
Фазовая
диаграмма.
Колебания затухли, значит, положение устойчиво.
1.2. Несимметричное смещение – вправо.
Положение устойчиво, т.к. колебания затухли.
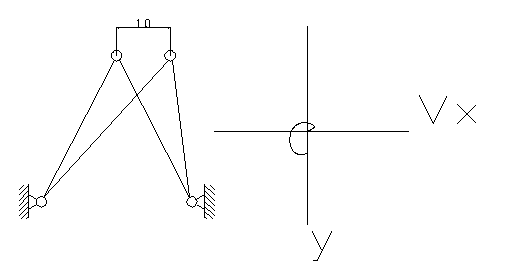
Системе придается начальная скорость.
1.3. Придание скорости в положении 1 по горизонтали. Величина скорости Vx=30,00.
Положение устойчиво.
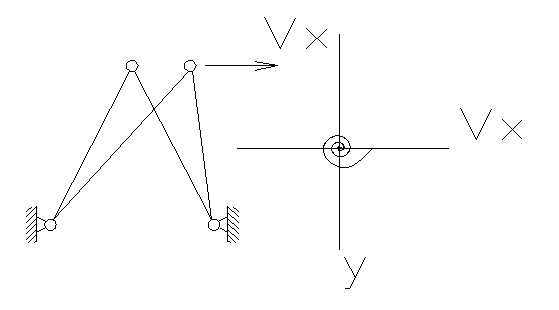
1.4.Придание скорости по вертикали Vу=30,00.
Положение устойчиво.
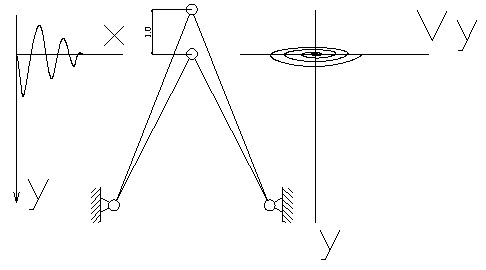
Выведение из равновесия положения.
1.5. По оси Х положение неустойчиво.
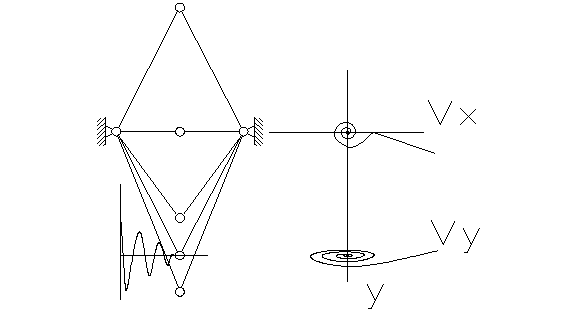
1.6.Положение неустойчиво по оси У.
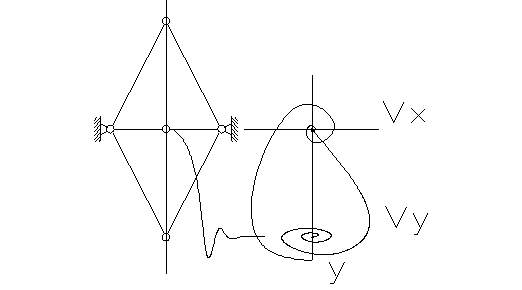
Часть 1.3. Нелинейное колебание Мизеса.
1.1.
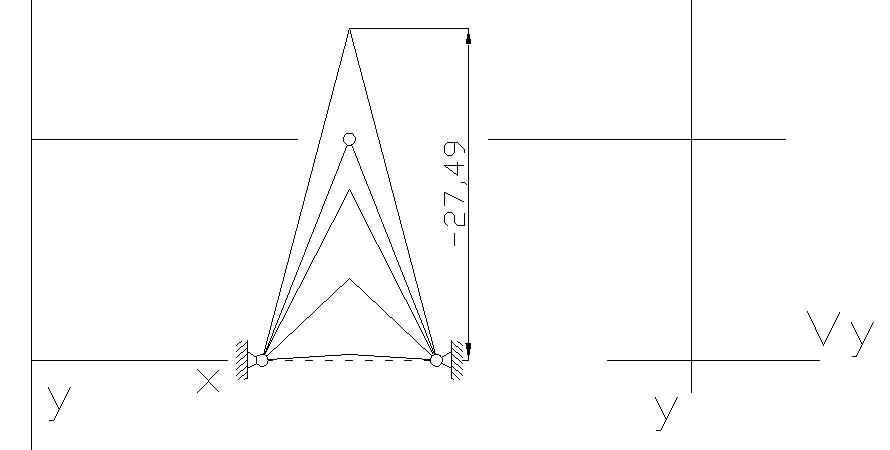
1.2.
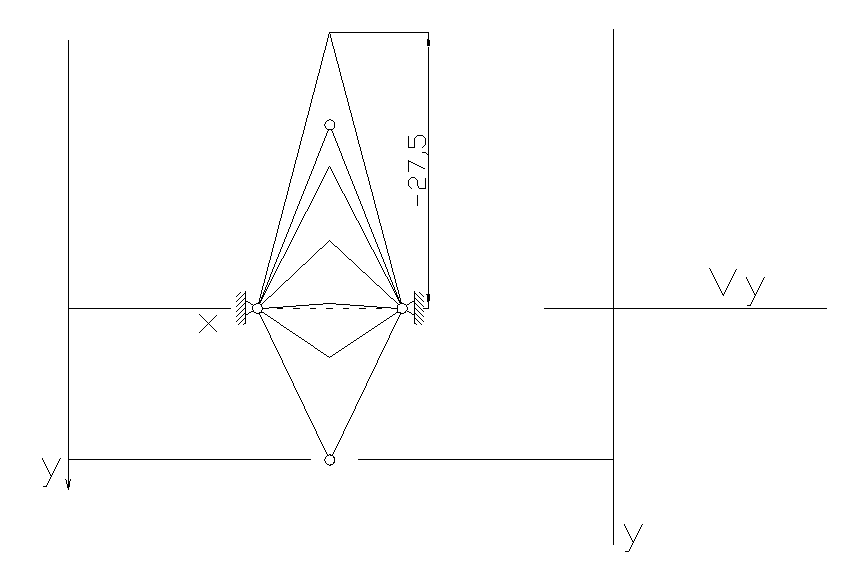
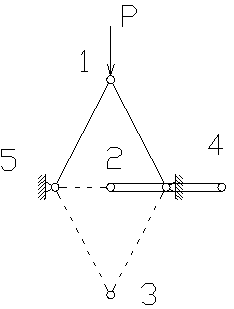
Часть 2.1. Исследование устойчивости системы от возрастающей нагрузки. Приложение силы Р=Р0· t/T, где Р0=10. Положение устойчиво.
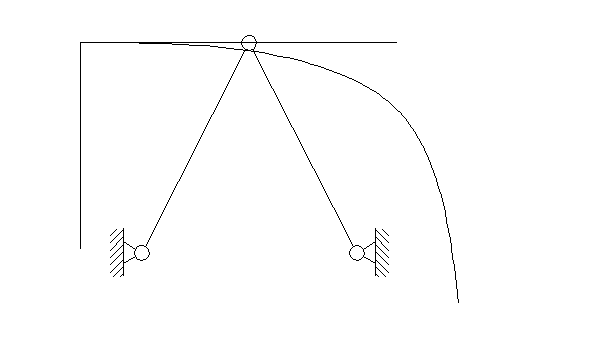
Находим значение критической силы Р0.
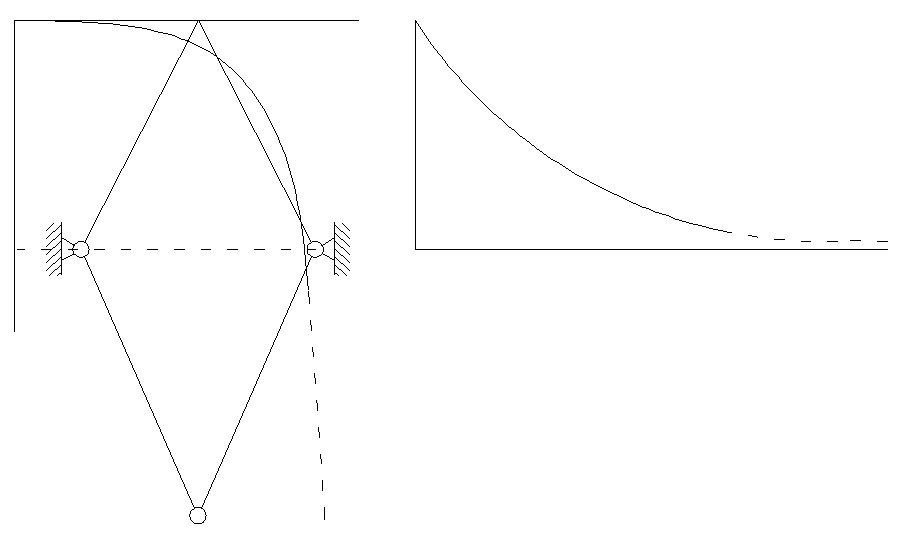
В нашем случае критическая сила равна Р0 = 865
Максимальное смещение равно У=23,7762
Часть 2.2. Высокая ферма.
Координаты точек (x;y):
т.1 (0;-18)
т.4 (4;0)
т.5 (-4;0)
l0 = 18,44.
EF = 1000.
Находим значение критической силы Р0.

В этом случае критическая сила равна Р0 = 1118
Максимальное смещение равно У=40,1450
При увеличении фермы критическая сила также возрастает.
Придадим ферме небольшое начальное возмущение Х0=0,1.
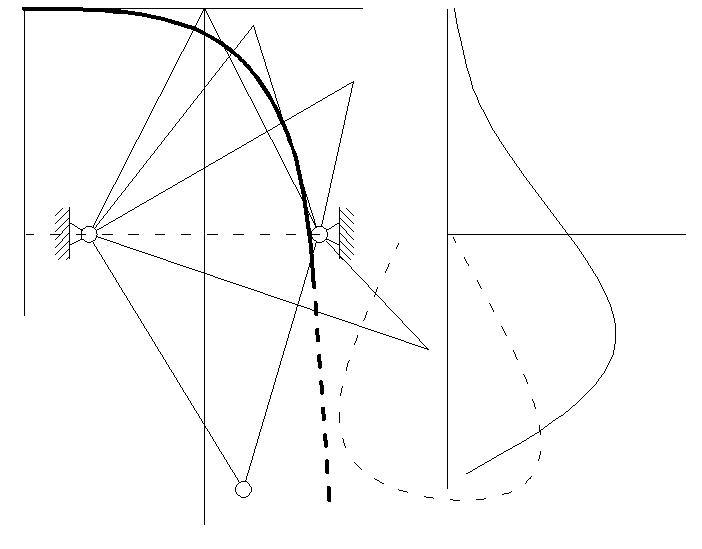
Получаем: - критическая сила меньше при начальном возмущении
- критическая сила сильно зависит от начальной формы равновесия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.