




3.2. Силовой расчёт рычажного механизма с учётом динамических нагрузок.
3.2.1 Построение плана ускорении:
Так как частота вращения ведущего звена постоянна (n1=const), то точки А и С имеют только нормальное ускорение. Которые будут равны между собой.
Величины ускорений определим по формуле:
аАn=ω12lОА; (25)
аАn=6,820,13=6,01 м/с2;
|
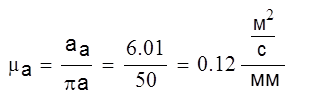 |
Из произвольной точки π строим вектора πа и πс. Эти вектора направлены к центру вращения, т.е. они направлены от точек А и С к точке О, параллельно звену АС.
Ускорение точек В и D определяются системой векторных уравнений:
аВ=аА+аВАτ+аВАn; аВ║ОВ. (27)
аD=аС+аСDτ+аCDn; аD║ОD. (28)
Ускорение точек А и С нам известно по величине и по направлению. Величины ускорений аВАn и аCDn мы можем определить из выражения:
аВАn=VВА2/AB=0,452/0,52=0,39 м/с2. (29)
aCDn=VCD2/CD=0,452/0,52=0,39 м/с2. (30)
Тогда длинны векторов, изображающих эти ускорения на плане ускорений будут равны:
an1= аВАn /μа=0,39/0,12=3,25 мм. (31)
сn2= аCDn /μа=0,39/0,12=3,25 мм. (32)
Определяем величины ускорений, умножая длины соответствующих им векторов на плане ускорений на масштабные коэффициенты:
аD=πd.μа=38.0,12=4,56 м/с2. (33)
Величины остальных ускорений определяем таким же образом. Результаты вычислений занесём в таблицу 8.
Таблица 8 – Значения ускорений:
|
Уско-рение |
аАn |
аВ |
аВАn |
аВАτ |
aS2 |
аСn |
aD |
aCDn |
aCDτ |
aS4 |
|
м/с2. |
6,01 |
1,92 |
0,39 |
5,16 |
4,44 |
6,01 |
4,56 |
0,39 |
5,28 |
4,8 |
3.2.2 Определение инертных нагрузок звеньев.
Силы инерции определим по формуле:
Pи=-mas; (34)
где m – масса звена; as – ускорение центра тяжести звена, м/с2. Знак минус показывает на то, что вектор Pи направлен противоположно вектору as.
PИ2= -26 . 4,44=-115,44 Н;
PИ3= -50 . 1,92=-96 Н;
PИ4= -26 . 4,8= -124,8 Н;
PИ5= -32 . 4,56= -145,92 Н.
На звенья 2 и 4 помимо сил инерции действуют ещё и моменты инерции:
Ми= -Is. ε; (35)
В соответствии с методическими указаниями, Is=0,1ml2; (36)
Тогда Is2=0,1.26.0,522=0,703 кг. м2;
Is4=0,1.26.0,522=0,703 кг. м2.
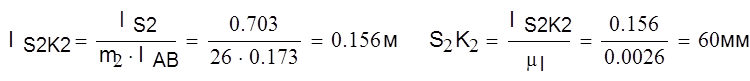 |
|
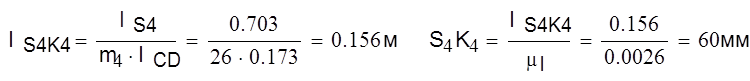 |
Вычерчиваем в масштабе звено 2. Откладываем в масштабе расстояние lS2K2 от точки S2 (точка К2 должна быть дальше от точки подвеса А, чем точка S2). Получим точку К2.
Уравнение силы инерции:
PИ= -maS= -maA-maSA. (38)
Решим данное уравнение графически. Для этого через точку S2 проводим прямую, параллельную ускорению аА (отрезку πа на плане ускорений), а через точку К2 прямую, параллельную ускорению аSA ( отрезку s2a на плане ускорений). Через точку пересечения этих прямых проводим прямую, параллельную ускорению аS2 и противоположно направленную. Это и будет линия действия силы инерции РИ2. Величина этой силы была вычислена ранее. Линию действия силы инерции РИ4 определяем аналогично.
Находим расстояния от точек подвеса до точек пересечения линий действия сил инерции со звеньями:
lAN2=AN2μl=42. 0,0026=0,109 м; (39)
lСN4=CN4μl=25. 0,0026=0,065м.. (40)
3.2.3. Определение силы тяжести звеньев.
Силы тяжести определяем по формуле:
Gi=mig; (41)
Где mi - масса звена, g – ускорение свободного падения.
GS2=26. 9,81=255,06 Н;
G3=50. 9,81=490,5 Н;
GS4=26. 9,81=255,06 Н;
G5=32. 9,81=313,92 Н.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.