Силовой расчёт рычажного механизма с учётом динамических нагрузок. Определение инертных нагрузок звеньев, страница 2

Сила тяжести звена 1 нам не дана, так как расчёты можно выполнить без её учёта.

3.2.4. Определение реакции в кинематических парах и уравновешивающей силы.

Определение реакции в кинематических парах начинается с группы звеньев, наиболее отдалённой от ведущего звена АС, т.е. с группы Ассура со звеньями 2 и 3, или 4 и 5. Начнём с рассмотрения группы со звеньями 2 и 3.

Вычерчиваем группу 2,3 ( в масштабе μ_l=0,0026 м/мм) и в соответствующих точках прикладываем все действующие силы. Отброшенные связи заменяем силами реакции R₁₂ⁿ и R₁₂ ^τ.

Запишем векторное уравнение равновесия:

G₃+F_св+P_И3+G_S2+P_И2+R₁₂ⁿ+R₁₂ ^τ =0.   (42)

Величину силы R₁₂ ^τ определим из уравнения моментов относительно точки В:

∑М_ib(F_i)= -R₁₂ ^τ AB-G_S2h₃+P_И2h₄=0.   (43)

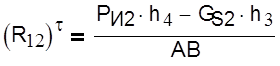Где h₃ и h₄ плечи сил. h₃=30 мм; h₄=143 мм.

Подставив численные значения получим:

Оставшуюся реакцию R₁₂ⁿ найдём из плана сил. План сил построим в соответствии с векторным уравнением. Принимаем масштабный коэффициент μ_р=10 Н/мм. Тогда: [R₁₂ ^τ]= R₁₂ ^τ/μ_р=44,3/5=8,86 мм.   (44)

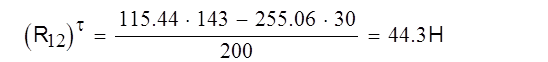Аналогично определим остальные значения длин векторов:

[G₃]= G₃/μ_р=490,5/5=98 мм;

[F_CB]= F_CB/μ_р=0/5=0 мм;

[P_И3]= P_И3/μ_р=96/5=19,2 мм;

[G_S2]= G_S2/μ_р=255,06/5=51 мм;

[P_И2]= P_И2/μ_р=115,44/5=23 мм.

Соединив конец вектора G_S2 с началом вектора Р_И3, получим вектор полной реакции R₁₂. Определим его величину:

 R₁₂= [R₁₂]^. μ_р=117^. 5=585 Н.

Составляющую определим, соединив конец вектора R₁₂ и начало вектора R₁₂ ^τ.

Вычерчиваем группу 4,5 ( в масштабе μ_l=0,0026 м/мм) и в соответствующих точках прикладываем все действующие силы. Отброшенные связи заменяем силами реакции R₁₄ⁿ и R₁₄ ^τ.

Запишем векторное уравнение равновесия:

G₅+F_CD+P_И5+G_S4+P_И4+R₁₄ⁿ+R₁₄ ^τ =0.   (45)

Величину силы R₁₂ ^τ определим из уравнения моментов относительно точки В:

∑М_iD(F_i)= R₁₄ ^τ CD+G_S4h₁-P_И4h₂=0.   (46)

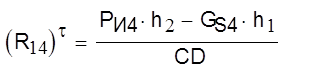Где h₁ и h₂ плечи сил. h₁=35 мм; h₂=93 мм.

Подставив численные значения получим:

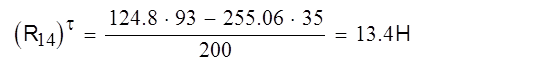Оставшуюся реакцию R₁₄ⁿ найдём из плана сил. План сил построим в соответствии с векторным уравнением. Принимаем масштабный коэффициент μ_р=80 Н/мм. Тогда: [R₁₄ ^τ]= R₁₄ ^τ/μ_р=13,4/80=0,16 мм.   (47)

Аналогично определим остальные значения длин векторов:

[G₅]= G₅/μ_р=313,92/80=4 мм;

[F_CD]= F_CD/μ_р=10080/80=126 мм;

[P_И5]= P_И5/μ_р=145,92/80=2 мм;

[G_S4]= G_S4/μ_р=255,06/80=3,18 мм;

[P_И4]= P_И4/μ_р=124,8/80=1,56 мм.

Соединив конец вектора P_И4  с началом вектора G_S4, получим вектор полной реакции R₁₄. Определим его величину:

 R₁₄= [R₁₄]^. μ_р=138^. 80=11040 Н.   (48)

Силовой расчёт ведущего звена АС.

Изобразим ведущее звено АС в масштабе μ_l=0,0026 м/мм. Приложим к нему все действующие на звено силы. Уравновешивающую силу F_ур приложим к точке С перпендикулярно ведущему звену АС. Запишем векторное уравнение равновесия:

R₀₁+R₂₁+R₄₁+F_ур=0.   (49)

Для определения уравновешивающей силы составим уравнение моментов относительно точки О.

∑М_iО(F_i)= R₄₁h₅+R₂₁h₆-F_урОС=0.   (50)

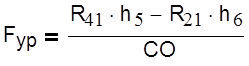Где h₅ и h₆ плечи сил. h₅=43 мм; h₆=49 мм.

Подставив численные значения получим:

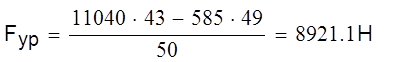Оставшуюся реакцию R₀₁ найдём из плана сил. План сил построим в соответствии с векторным уравнением. Принимаем масштабный коэффициент μ_р=80 Н/мм. Тогда: [R₄₁]= R₄₁/μ_р=11040/80=138 мм.

Аналогично определим остальные значения длин векторов:

[R₂₁]= R₂₁/μ_р=585/80=7,31 мм;

[F_ур]= F_ур/μ_р=8921,1/80=111,5 мм.

Соединив конец вектора R₂₁ с началом вектора F_ур, получим вектор полной реакции R₀₁. Определим его величину:

 R₀₁= [R₀₁]^. μ_р=72^. 80=5760 Н.

3.2.5. Определение уравновешивающей силы по методу проф. Н.Е. Жуковского.

В произвольном масштабе строим повёрнутый на 90⁰ (в любую сторону) и в соответствующих точках плана прикладываем все внешние силы и силы инерции звеньев. Составляем уравнение моментов относительно полюса повёрнутого плана скоростей, беря плечи по чертежу в мм.

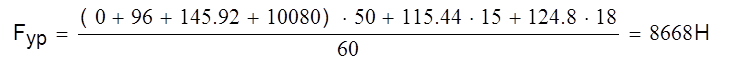∑М_ip(F_i)= -F_CB 50-F_И350-P_И215-P_И550-F_CD 50-P_И418+ F_ур60=0.   (51)

(52)

Определяем расхождение результатов:

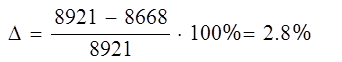Расхождение результатов в пределах нормы.