













Задача №1.
Рассчитать зубчатые колеса одноступенчатого планетарного редуктора и подобрать электродвигатель, который соединяется с входным валом солнечной шестерни посредством упругой муфты (рисунок 1). Мощность на выходном валу редуктора Р3 = 9 кВт, угловая скорость этого вала ω3 = 18 рад/с. Срок службы редуктора 45 000 ч. Пусковая нагрузка 140% от номинальной. Число сателлитов — 3. Недостающие данные принять самостоятельно.
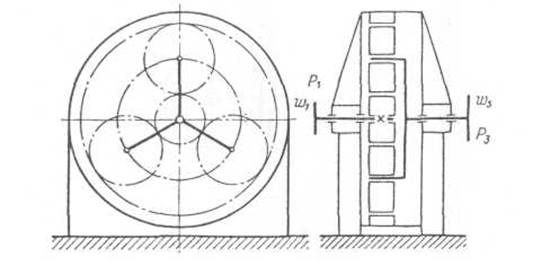
Рисунок 1 – Схема одноступенчатого планетарного редуктора.
Решение:
Примем передаточное отношение i = 4, тогда:
n1 = n3 · i
w1 = w3 · i = 18 · 4 = 72 рад/с.
n1 = ![]() =
= ![]() =
688 об/мин.
=
688 об/мин.
n3 = ![]() =
= ![]() =
172 об/мин.
=
172 об/мин.
Требуемая мощность электродвигателя определяется по формуле:
Ртр
= ![]() =
= ![]() =
9,47 кВт.
=
9,47 кВт.
η – общий КПД привода;
η = η1 · η2 = 0,97 · 0,99 = 0,95
η1 = 0,97 – КПД одноступенчатого планетарного редуктора (табл. 5.1 [4]);
η1 = 0,99 – КПД, учитывающий потери в опорах вала (табл. 1.1 [4]).
По приложению П1 [4] выбираем электродвигатель 4А160М6 ГОСТ 19523-81, у которого N = 15,0 кВт, n = 1000 об/мин, ς = 2,6%, nном = 1000–26 = 974 об/мин.
Вращающий момент на ведомом валу:
Т3 =
![]() =
= ![]() =
88,3 Н·м.
=
88,3 Н·м.
Число зубьев солнечного колеса Z1 = 30.
Число зубьев саттелита находим по формуле (формула 5.2 [4])
Z2 = 0,5 · Z1 · (i1н(3) – 2) = 0,5 · 30 · (4 – 2) = 30.
Проверим выполнение условия вхождения зубьев в зацепление по формуле (формула 5.10 [4]):
![]() =
= ![]() = 40 – целое число, следовательно,
условие выполнено.
= 40 – целое число, следовательно,
условие выполнено.
Проверим выполнение условия соседства по формуле (формула 5.10 [4]):
(Z1 + Z2) · sin![]() ≥ Z1 + 2
≥ Z1 + 2
(30 + 30) · sin![]() ≈ 52 > 30 +
2 = 32 – условие выполнено.
≈ 52 > 30 +
2 = 32 – условие выполнено.
Число зубьев корончатого колеса из условия соосности определяется по формуле (формула 5.2 [4]):
Z3 = Z1 + 2 · Z2 = 30 + 2 · 30 = 90.
Выбираем для зубчатых колес сталь 40ХН, улучшенную, со средней твердостью НВ 220 (табл. 3.3 [4]).
Базовое число циклов перемены напряжений:
Nно = 2,3 · 102 = 230 (табл. 3.2 [4]).
Рабочее число циклов перемены напряжений для солнечного колеса за весь срок службы определяется по формуле:
Nн = 60 · ne · n1(H) · t = 60 · 3 · 974 · 45000 = 7,9 · 109 циклов
n1(H) = n1(3) – n(3) = 974 – 172 = 802 об/мин
Так как Nн > Nно, то принимаем коэффициент долговечности КHL = 1.
Межосевое расстояние между солнечным колесом и саттелитом определяется по формуле (формула 5.15 [4]):
aw ≥ Ka · (U + 1) · 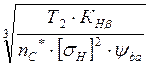
Ka = 49,5 – для передач с прямозубыми цилиндрическими колесами;
U
= ![]() =
= ![]() =
1 – передаточное число;
=
1 – передаточное число;
Т2
= ![]() =
= ![]() =
22 · 103 – вращающий момент;
=
22 · 103 – вращающий момент;
КНβ = 1,2 – коэффициент концентрации нагрузки (по табл. 3.1 [4]);
nc* = nc – 0,7 = 3 – 0,7 = 2,3 – расчетное число саттелитов;
[σH] – допускаемое контактное напряжение, определяется по формуле (формула 5.15 [4]):
[σH] = ![]() =
= ![]() =
573 МПа,
=
573 МПа,
σН lim b – предельное значение контактной выносливости (табл. 3.2 [4])
σН lim b = 2 · НВ + 70 = 2 · 220 + 70 = 510 МПа
[SH] – коэффициент безопасности (1,1÷1,2) для колес из улучшенной стали;
ψ = 0,5 – коэффициент ширины саттелита;
aw ≥ 49,5 · (1 + 1) · 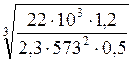 = 40,79 мм.
= 40,79 мм.
Примем aw = 50 мм.
Модуль зацепления находим по формуле (формула 3.14 [4]):
m
= ![]() =
= ![]() =
1,6 примем
m=
2.
=
1,6 примем
m=
2.
Находим диаметры делительных окружностей колес и их ширину:
d1 = m· Z1 = 2 · 30 = 60 мм;
d2 = m· Z2 = 2 · 30 = 60 мм;
d3 = m · Z3 = 2 · 90 = 180 мм;
b= ψba · aw = 0,5 · 50 = 25 мм.
Выполним проверочный расчет на изгиб по формуле (формула 5.21 [4]):
Расчетное напряжение изгиба:
σF = 2 · YF ·Yβ ·
YV · ![]() = 2 · 3,8 · 0,6 · 0,1 ·
= 2 · 3,8 · 0,6 · 0,1 · ![]() = 26,16 МПа
= 26,16 МПа
[σF] = ![]() =
= ![]() =
465 МПа
=
465 МПа
σF = 26,16 МПа < [σF] = 465 МПа – условие выполняется.
σFmax = 1,4 · σF = 26,16 · 1,4 = 36,62 МПа ≤ [σFmax]
Контактные напряжения находим по формуле:
σН = ZM ·
Zn ·
Zε · 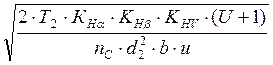
ZM =
275 ![]() ;
Zn =
1,76; Zε =
0,9 (3, стр.31).
;
Zn =
1,76; Zε =
0,9 (3, стр.31).
КНα = 1; КНβ = 1,2; КНV = 1,1 (3, стр.32).
σН = 2,75 · 1,76 · 0,9
· 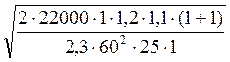 = 3,26 МПа.
= 3,26 МПа.
σН = 3,26 МПа < [σН] = 550 МПа.
σНmax = 1,4 · σН = 1,4 · 3,26 = 4,57 МПа < [σНmax] = 3,1 · σH = 3,1 · 690 = 2139 МПа.
σH = 690 МПа (табл. 3.3 [3]).
Задача №2.
Привод к цепному транспортеру состоит из электродвигателя 1, упругой муфты 2, червячного редуктора 3 и цепной передачи 4 (рисунок 2). Подобрать электродвигатель, разбить общее передаточное число по ступеням привода и рассчитать червячную передачу. Окружное усилие F = 11 кН, на ведущей звездочке 5 транспортера, скорость цепи v = 0,4 м/с и диаметр звездочки D = 275 мм.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.