Схема одноступенчатого планетарного редуктора. КПД одноступенчатого планетарного редуктора. Вращающий момент на ведомом валу, страница 2

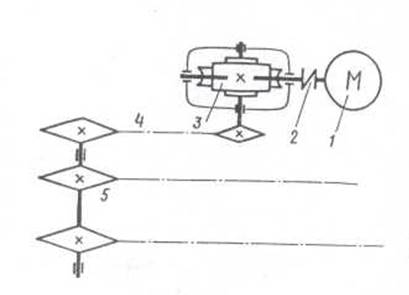
Рисунок 2 – Схема цепного транспортера.

Решение:

Примем предварительно КПД червячного редуктора η = 0,8.

Угловая скорость транспортера находится по формуле:

w_тр =  =  = 2,91 рад/с.

Частота вращения транспортера находится:

n_тр =  =  = 27,8 об/мин.

Мощность на валу транспортера определяется по формуле:

Р_тр = F · v = 11 · 10³ · 0,4 = 4,4 кВт.

Общий КПД привода находим по формуле:

η = η₁ · η₂ · η₃ · η₄³

где     η₁ = 0,8 – КПД червячного редуктора;

η₂ = 0,92 – КПД цепной передачи;

η₃ = 0,98 – КПД муфты;

          η₄ = 0,99 – КПД, учитывающий в опорах валов.

η = 0,8 · 0,92 · 0,98 · 0,99³ = 0,7

Определяем требуемую мощность электродвигателя по формуле:

Р =  =  = 6,3 кВт.

По приложению П3 [4] выбираем электродвигатель 4А112М2 с мощностью   N = 7,5 кВт, n = 3000 об/мин и ς = 2.

Для цепной передачи U_ц.п. = 3,0; для червячного редуктора U_чр = 20,0, тогда общее находится по формуле:

U_общ = U_ц.п. · U_чр = 3 · 20 = 60

Угловая скорость электродвигателя определяется по формуле:

w_дв = U_общ · w_тр = 60 · 2,91 = 174,6 рад/с.

Частота вращения электродвигателя определяется по формуле:

n_дв = U_общ · n_тр = 60 · 27,8 = 1668 об/мин.

Номинальную частоту вращения электродвигателя определим по формуле:

n_ном = 3000 – 30 = 2970 об/мин.

Уточним найденные значения:

U_общ =  =  = 106,8; U_ц.п. =  =  = 5,34.

При U_чр = 20; Z₁ = 2 (4, стр. 55), число зубьев червячного колеса определим из формулы:

Z₂ = Z₁ · U_чр = 2 · 20 = 40 (табл. 4.1 [4]).

Материал червяка – сталь 45 с закалкой до твердости не менее 45 HRC и последующим шлифованием. Для червячного колеса – бронза Бр.АЖ9-4Л (с отливом в песчаную форму). Примем v_s ≈ 7,5 м/с. При длительной работе допускаемое контактное напряжение [σ_н] = 140 Н/мм² (табл. 4.9 [4]). Допускаемое напряжение изгиба для нереверсивной работы определим по формуле:

[σ_0F] = K_FL · [σ_0H]^*

Определим суммарное число циклов перемен напряжений:

N_Σ = 60 · n₂ · t

где     n₂ – частота вращения червячного колеса;

[σ_0H]^* = 98 – по табл. 4.8 [4].

N_Σ = 60 · 24000 · 83,5 = 120,24 · 10⁶.

n₂ =  =  = 148,5 об/мин.

K_FL = 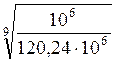 = 0,587

[σ_0F] = 0,587 · 98 = 58 МПа.

Примем коэффициент диаметра червяка g = 10, коэффициент нагрузки k = 1,2.

Вращающий момент на валу червячного колеса определим по формуле:

Т₂ =  =  = 1,11 · 10³ Н·м.

Р₂ = Р₁ · η₁ · η₄ = 6,11 · 0,8 · 0,99 = 4,84 кВт.

w₂ =  =  = 8,73 рад/с.

Р₁ = Р · η₃ · η₄ = 6,3 · 0,98 · 0,99 = 6,11 кВт.

Т₁ =  =  = 35 Н·м

Межосевое расстояние находим из условия выносливости по формуле (формула 4.19 [4]):

a_w = () ·  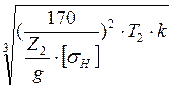= () ·  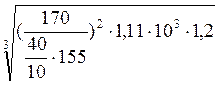= 232,2 мм.

модуль =  =  = 9,3 мм.

По ГОСТ 2144-76 выбираем m = 10 мм, g = 10 мм.

Уточним:

a_w =  =  = 250 мм.

Делительный диаметр определим по формуле:

d₁ = g · m = 10 · 10 = 100 мм.

Диаметр вершин витков червяка находим по формуле:

d_a1 = d₁ + 2 · m = 100 + 2 · 10 = 120 мм.

Диаметр впадин витков червяка определим из формулы:

d_f1 = d₁ – 2,4 · m = 100 – 2,4 · 10 = 76 мм.

Длина нарезанной части шлифованного червяка определяется по формуле (формула 4.7 [4]):

b₁ ≥ (11 + 0,06 · Z₂) · m + 25 = (11 + 0,06 · 40) · 10 + 25 = 159 мм.

Принимаем b₁ = 160 мм.

Делительный угол подъема витков γ (по табл. 4.3 [4]) и при Z₁ = 2, g = 10 составляет – γ = 11°19'.

Дополнительный диаметр червячного колеса найдем из формулы:

d₂ = Z₂ · m = 40 · 10 = 400 мм.

Диаметр вершин зубьев червячного колеса определяется по формуле:

d_a2= d₂ + 2 · m = 400 + 2 · 10 = 420 мм.

Диаметр впадин зубьев червячного колеса определим из формулы:

d_f2 = d₂ – 2,4 · m = 400 – 2,4 · 10 = 376 мм.

Наибольший диаметр червячного колеса:

d_aн2 = d_a2 +  = 420 +  = 435 мм.

Ширину венца червячного колеса определим из формулы (формула 4.12 [4]):

b₂ = 0,75 · d_a1 = 0,75 · 120 = 90 мм.

Определим окружную скорость червяка по формуле:

v₁ =  =  = 15,5 м/с.

Следовательно, КПД редуктора принят правильно.

По табл. 4.7 [4] выбираем 7-ую степень точности передачи. Коэффициент динамичности К_v = 1,1.

Коэффициент неравномерности распределения нагрузки определяется по формуле (формула 4.26 [4]):

К_β = 1 + ()³ · (1 – х)

По табл. 4.6 [4] находим Θ = 86, х = 0,6 (4, стр. 65).

К_β = 1 + ()³ · (1 – 0,6) ≈ 1,04