Коэффициент нагрузки найдем из соотношения:
К = Кβ · Кv = 1,04 · 1,1 = 1,14
Контактное напряжение определим по формуле (формула 4.23 [4]):
σН
= 
= 
=
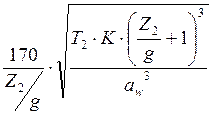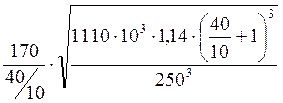135,22 МПа.
σН = 135,22 МПа < [σН] = 141 МПа.
Δσ = 
· 100% = 
· 100% = 4,1%.
Проверка прочности зубьев червячного колеса на изгиб:
Эквивалентное число зубьев
Zv = 
= 
= 42,9.
Коэффициент формы зуба определим по табл. 4.5 [4]. YF = 2,24.
Напряжение изгиба определим по формуле (формула 4.24 [4]):
σF = 
= 
=
9,45 МПа.
σF = 9,45 МПа < [σF] = 58 МПа.
Проведем проверку на статическую прочность по изгибу:
σF1max ≤ [σF1]max
[σF1]max = 0,8 · σT – допускаемое максимальное напряжение на изгиб для зубьев червячного колеса.
[σF1]max = 0,8 · 200 = 160 МПа.
σF1max = 1,5 · σF1 = 1,5 · 9,45 ≈ 14,2 МПа < [σF1]max = 160 МПа.
Условия прочности выполняются.
Задача №3.
По данным задачи 2 рассчитать выходной тихоходный вал червячного редуктора и подобрать по нему подшипники качения. Дать рабочий эскиз вала. Недостающие данные принять конструктивно.
Решение:
Диаметр выходного конца тихоходного вала червячного колеса определим по формуле:
db =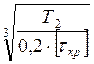 
= 
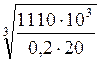= 65,2
мм.
[τкр] – допускаемое напряжение при кручении.
Примем db = 66 мм.
Диаметр под подшипник примем dп = 70 мм.
Диаметр под колеса примем dк = 75 мм.
Силы, действующие в зацеплении находим по формулам:
окружная
Ft2 = 
= 
=
5550 H.
радиальная
Рисунок 3. Fr2 = Ft2 · tgα = 5550 · tg20o = 2020 H.
осевая
Fа2 = 
= 
=
700 H.
Выбираем подшипники роликовые конические однорядные по ГОСТ 333-79 средней серии № 7314, d = 70 мм, D = 150 мм, В = 37 мм, С = 165 кН, Со = 134 кН, e = 0,31, Y = 1,937.
Находим реакции опор:
в плоскости XOZ
Rz3 = Rz4 = 
= 
=
2775 H.
в плоскости YOZ
Ry3 · l2 + Fr2 · 
– Fa2 · 
= 0.
Ry3 = 
= – 660 H.
Ry4 · l2 – Fr2 · – Fa1 · = 0.
Ry4 = 
= 1360 H.
Проверка: Ry3 – Ry4 + Fr2 = – 660 – 1360 + 2020 = 0.
Находим изгибающие моменты:
в плоскости ХOZ
Мz4 = 0, Mz3 = 0, Mz2 = – Rz3 · = – 2775 · 
=
555 H·м.
в плоскости YOZ
Мy3 = 0, My4
= 0, My2 = Fa2 · + Ry4 · = 700 · + 1360 · = 412 Н·м.
Определяем суммарные реакции:
R3 = 
= 
= 2852,4 H.
R4 = 
= 
= 3090,3 H.
Осевые составляющие радиальных реакций конических подшипников определяем по формуле (формула 9.9 [1]):
φ3 = 0,83 · е · R3 = 0,83 · 0,31 · 2852,4 = 733,9 H.
φ4 = 0,83 · е · R4 = 0,83 · 0,31 · 3090,3 = 795,1 H.
φ3 < φ4,
Ra3 = Fa> φ4 – φ3, тогда Ra3= φ3 = 733,9 Н.
Ra4= φ3 + Fa = 733,9 + 700 = 1433,9 H.
= 
= 0,257 < e, осевые
силы не учитываем.
Находим эквивалентную нагрузку по формуле:
Rэ3 = R3 · v · Kσ · Kτ = 2852,4 · 1 · 1 · 1,3 = 3708,1 H.
= 
=
0,464 > e, осевые силы учитываем, x = 0,4, y = 1,937.
Rэ4 = (x · R4 + y · Ra4) · Kτ · Kσ = (0,4 · 3090,3 + 1,937 · 1433,9) · 1,3 · 1 = 5317,7 H.
Находим расчетную долговечность по формуле (формула 9.1 [1]):
L = (
)
= (
) =
89187
млн. об.
Ln = 
= 
= 10 · 106 ч.
Найденная долговечность приемлема.
Проверим шпоночное соединение на смятие:
[σсм] = 120 МПа – при стальной ступице.
Диаметр вала под червячным колесом 75 мм, b · h · L = 18 x 11 x 90, t1 = 7мм.
σсм
= 
= 
=
102,8 МПа < [σсм] = 120 МПа.
Определим коэффициент запаса прочности в месте посадки зубчатого колеса.
Суммарный изгибающий момент находим по формуле:
М = 
= 
=
691,2 Н·м.
Кσ = 1,6 и Кτ = 1,5 (из табл. 8.5 [1]), εσ = 0,76 и ετ = 0,65 (из табл. 8.8 [1]).
Момент сопротивления нетто найдем по формуле:
Wнетто= 
= 
= 46507 мм3.
Находим амплитуду нормальных напряжений изгиба.
σv = 
= 
= 14,86 МПа.
Определим момент сопротивлению кручению сечения нетто по формуле:
Wкр. нетто = 
= 
=
78908,8 мм3.
Находим амплитуду и среднее напряжение цикла касательных напряжений по формуле:
τv = τm
= 
= 
=
14,1 МПа.
Определяем коэффициент запаса прочности по формуле:
σ-1 = 0,43 · σв = 0,43 · 570 = 246 МПа.
где σв = 570 МПа – для стали 45 нормализованной.
τ-1 = 0,5 · σ-1 = 0,58 · 246 = 142 МПа.
Sσ =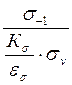 
= 
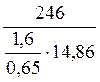= 6,73
Sτ =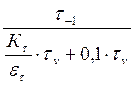 
= 
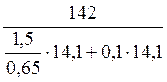= 4,18
Находим результирующий коэффициент запаса прочности по формуле:
S =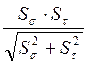 
=
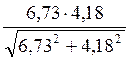= 3,55 > [S] = 1,5 ÷
3,0.
Полученное значение достаточно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.