Законы изменения токов. Расчёт переходного процесса классическим методом. Временная диаграмма напряжений

Формулировка задания   (IV семестр, 13 вариант, переходные процессы)

1.  Найти законы изменения токов i₁(t), i₂(t), i₃(t) и напряжений на ёмкости u_c(t). Задачу решить классическим и операторным методами.

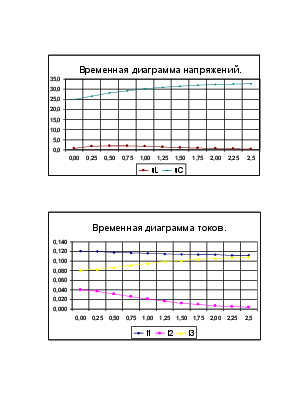
2.  Построить временные диаграммы токов i₁(t), i₂(t), i₃(t) и напряжений u_c(t).

3.  Составить математическую модель переходного процесса по методу переменных состояния и подготовить полученную систему дифференциальных уравнений для расчёта на ЦВМ.

Исходные данные

E = 100 B,

R₁ = 600 Ом,

R₂ = 600 Ом,

R₃ = 600 Ом,

С = 0.6 МкФ,

L = 0.01 Гн.

Ключ замыкается.

Найти: i₁(t), i₂(t), i₃(t),u_c(t).!Синтаксическая ошибка, (

          Решение

Расчёт переходного процесса классическим методом.

1.  Составим систему уравнений для момента времени после коммутации.

i₁ - i₂ - i₃ = 0,

R₁i₁ + u_c = E,

- u_c + R₃i₃ + L= 0,                          (*)

i₂ = C.

2.  Эту систему уравнений сведём к одному дифференциальному уравнению второго  порядка относительно напряжения u_c.

Из второго уравнения системы (*): i₁ = .            (1)

Из первого уравнения системы (*): i₃ = i₁ - i₂ .                       (2)

Подставим в уравнение (2) полученное уравнение (1) и четвёртое уравнение системы (*), получим: i =  - C .                           (3)

Продифференцируем уравнение (3):  = -  - C .           (4)

Подставим уравнение (4) в третье уравнение системы (*), получим:

                  -u_c + R₃   - C  - L  -- C  = 0,

-u_c +  -  - R₃C -  - LC = 0,

LC+   + R₃C   +   1 +  u_c = ,

+ + u_c = .               (5)

3.    Определим начальные условия. Найдём ток в индуктивности и напряжение на ёмкости до коммутации.

i₃(0_-) = ;                 u_c(0_-) = .

По законам коммутации:

i₃(0_-) = i₃(0_-) = ,                                                   (6)

u_c(0_-) = u_c(0) = .

4.  Для определения постоянных интегрирования необходимо знать значение производной  в момент  коммутации, т.е. при t = 0.

Из уравнения (3): = - .                                                         (7)

Необходимо знать  _{t=0 .}

Следовательно, в момент коммутации:   _t=0 = - .

Учитывая начальные условия (6) получаем:

                 _t=0 = - -  = .     (8)

5.  Определим корни характеристического уравнения.

Характеристическое уравнение имеет вид:    a² + 2da + (w₀)² = 0, где d = ,          w₀ = .                                              (9)

Подставим числовые значения:

d = » 16388.9,

w₀ = » 15811.4 .

Так как w₀<d, то корни характеристического уравнения будут вещественными отрицательными:

P₁ = -d + ,             P₂ = -d - .                          (10)

Подставим числовые значения:

P₁ = -16388.9 + » -12077 ,

P₂ = -16388.9 - » -20701 .

6.  Определим принуждённую составляющую искомой величины и запишем решение в общем виде.

После окончания переходного процесса: u_{c пр} =  .                  (11)

Общее уравнение имеет вид: u_с(t) = u_{c пр} + u_{c св} =  + А₁е^P1t + А₂е^P2t.              (12)

7.    Определим постоянные интегрирования А₁ и А₂.

Из выражения (12) при t = 0, находим

                 u_с(0) =  + А₁ + А₂,                                           (13)

                 _t=0 = P₁A₁ + P₂A₂ .

Подставляя начальные условия (6) и (8), получаем:

                  =  + А₁ + А₂,                                (14)

= P₁A₁ + P₂A₂ .

ð  А₂ =  - A₁ ,

-  = A₁ +  - A₁ ,

-  -  = A₁ . (15)

Подставляя числовые значения, получаем:

A₁ =  -  -  =

60 - 80 + 8.1 = -11.9 .

А₂ = = 3.6

Проверим найденные значения.

При  t = 0:     

u_с(0) =  =  = 25 В,

По формуле (13) u_с(0) =  + А₁ + А₂ =  - 11.9 + 3.6 = 25 В.

При  t = ∞:

u_с(∞) =  =  » 33.3 В,

По формуле (13) u_с(∞) =  =  » 33.3 В.

Следовательно, найденные значения верны.

Запишем окончательное решение: u_с(t) =  + А₁е^P1t + А₂е^P2t .

Подставив числовые значения получаем: u_с(t) = 33.3 – 11.9е^-12077t + 3.6e ^–20701t  В. (16)

7.  Определим остальные токи и напряжение u_L из исходной системы уравнений (*).

Из второго уравнения системы (*): i₁ = , тогда

i₁ = = 0.111 – 0.02е^-12077t – 0.01e ^–20701t  А.

Из четвёртого уравнения системы (*): i₂ = C, тогда

i₂ = С(A₁P₁e^P1t + A₂P₂e^P2t) = 0.6*10^-6(11.9*12077e^-12077t – 3.6*20701.6e^-20701t) =

= 0.09e^-12077t – 0.05e^-20701t  А.

Из первого уравнения системы (*): i₃ = i₁ - i₂ , тогда

i₃ = 0.111 + 0.02e^-12077t– 0.01e^-20701t - 0.09e^-12077t + 0.05e^-20701t  =