Балтийский государственный технический университет
им. Д.Ф.Устинова «ВОЕНМЕХ»
Кафедра электротехники.
Курсовая работа
по электротехнике.
Тема: ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ.
Вариант № 5
Студент:
Группа: Н 531
Преподаватель:
Оценка:
Подпись:
Санкт-Петербург 2005.
Содержание:
стр.
1. Исходные данные_______________________________________________3
2. Составление характеристического уравнения по Zвх.____________________________4
3. Расчет принужденных составляющих______________________________5
4. Определение начальных условий:
4.1 независимые начальные условия________________________________6
4.2 зависимые начальные условия__________________________________7
5. Составление дифференциального уравнения по законам Кирхгофа______8
6. Составление дифференциального уравнения методом Д-алгебраизации__9
7. Анализ полученного дифференциального уравнения_________________10
8. Решение полученного дифференциального уравнения классическим методом_________________________________________________________11
9. Определение остальных токов и напряжений_______________________12
10. Таблица проверок_____________________________________________13
11. Решение полученного дифференциального уравнения операторным методом_________________________________________________________14
12. Расчет дифференциального уравнения методом переменных состояния_17
13.Расчет переходных процессов, составленных методом переменных состояния с помощью программы MathCad._______________________________________19
14. Графики iL и uC, полученные методом переменных состояния_________20
15. Графики остальных токов и напряжений___________________________21
16 Проверка выполнения з.К. при t=2.5*![]() ___________________________22
___________________________22
Список используемой литературы________________________________23
1. Исходная схема задания
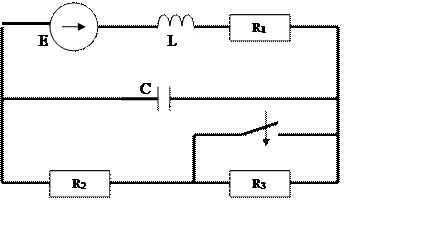
E=140 В R1=500 Ом R2=800 Ом R3=700 Ом C=0,8 мкФ L=0,03 Гн
2.Cоставление характеристического уравнения по Zвх
Составляем комплексное входное сопротивление относительно зажимов источника питания
R2* 1/jωC
![]() Z(jω)= +
jωL + R1 (1)
Z(jω)= +
jωL + R1 (1)
R2 + 1/jωC
Прировняем jω= a решим относительно него уравнение при Zвх = 0
R1R2 C + L R1 + R2
![]()
![]() a2 + * a +
=0 (2)
a2 + * a +
=0 (2)
R2 L C R2 L C
Обозначим
R1R2 C + L
![]() А =
А =
R2 L C
R1 + R2
![]() В=
В=
R2 L C
А = (500* 800*0.8* ![]() +0.03)/(800*0.8*
+0.03)/(800*0.8*![]() *0.03)=18229 (3)
*0.03)=18229 (3)
B = ( 500+800)/(800*0.8*![]() *0.03)=6.7708*
*0.03)=6.7708*![]() (4)
(4)
а2+А*а+ B=0 (5)
получим корни характеристического уравнения а1= -5194,54 (6)
а2= -13034,46 (7)
3. Определение принужденных составляющих
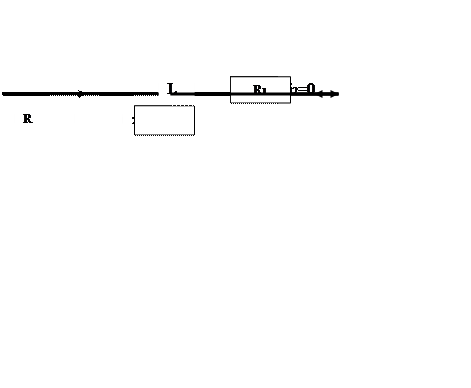
Можно нарисовать эквивалентную схему при устоявшемся режиме
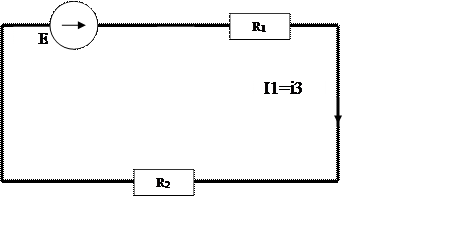
Рассчитаем токи и напряжения по законам Ома в остальных ветвях
i2пр=0 (8)
i1пр= ![]() = 0.1077 А
= 0.1077 А
i3пр=![]() = 0.1077 А (9)
= 0.1077 А (9)
uR1пр=![]() = 53.85 В (10)
= 53.85 В (10)
uR2пр= ![]() = 86.16В
= 86.16В
uСпр =![]() = 86.16В (11)
= 86.16В (11)
4.Определение начальных условий
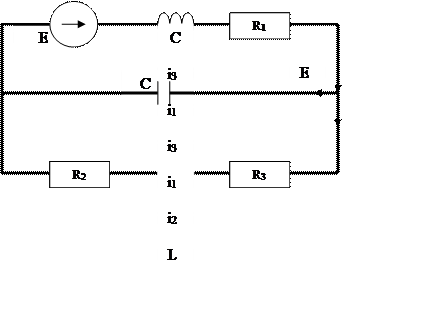
|
4.1.Определение ННУ
по первому закону коммутации
iL(_0)= ![]() = 0,07
А = iL(0) (13)
= 0,07
А = iL(0) (13)
по второму закону коммутации
uC(_0)=![]() = 105
В =uC(0) (14)
= 105
В =uC(0) (14)
iL(_0) = i1(_0) = i3(_0)
i2(_0)=0 т к конденсатор не пропускает постоянный ток
uR1(_0)= ![]() = 35 В
= 35 В
uR2(_0)=![]() = 56 В
= 56 В
uL(_0)=0 катушка при постоянном токе является закороченным проводником
4.2. Определение ЗНУ
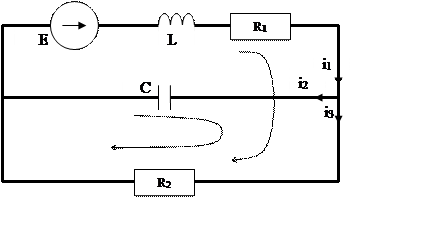
Стрелки указывают направление обхода контуров
Система уравнений по законам Кирхгофа
![]()
i1(0)= i2(0)+ i3(0) (15)
L*![]() + i1(0)*R1+
i3(0)*R2=E (16)
+ i1(0)*R1+
i3(0)*R2=E (16)
i3(0)*R2-(Uc(0)-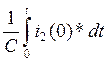 )=0 (17)
)=0 (17)
|

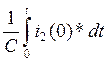 =0 (18)
=0 (18)
i3(0)*R2-Uc(0)=0
à i3(0)=![]() =0,1312 A (19)
=0,1312 A (19)
i1(0)=
i2(0)+ ![]() à
à
i2(0)=i1(0)-![]() =iL(0)-
=iL(0)-![]() =
= ![]() -
- ![]() = -
= -![]() = -0,0612 А (20)
= -0,0612 А (20)
L*![]() + i1(0)*R1+
+ i1(0)*R1+![]() =E à
=E à
![]() =
=![]() * ( E - iL(0)*R1-
* ( E - iL(0)*R1-![]() ) =
) =
|
35=uR1(_0) = uR1(0)=i1(0)*R1=35 нет скачка т к i1(0) =iL(0) не изменяется по первому закону Коммутации 56=uR2(_0) ≠ uR2(0)=i3(0)*R2=105 скачок
0,07=i3(_0) ≠ i3(0)=0,1312 скачок
0=i2(_0) ≠ i2(0)=-0,0612 скачок
0= uL(_0)
= L*![]() = 0 à нет скачка
= 0 à нет скачка
5.Составление дифференциального уравнения по законам Кирхгофа
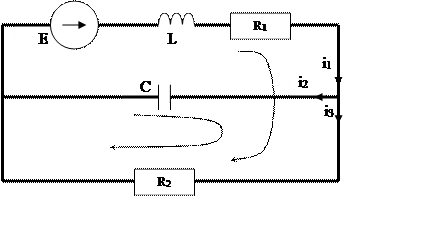
Стрелки указывают направление обхода контуров по законам Кирхгофа
![]()
i1= i2+ i3 (22)
L*![]() + i1*R1+
i3*R2=E (23)
+ i1*R1+
i3*R2=E (23)
i3*R2-(Uc(0)-
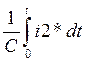 )=0 (24)
)=0 (24)
![]() *R2=
*R2=![]() *i2 продифференцируем уравнение (24)
*i2 продифференцируем уравнение (24)
i2= C*R2*![]() по (23) выразим i3 (25)
по (23) выразим i3 (25)
i3= ![]() -
- ![]() -
- ![]() по уравнению (25) выразим i2
через i1 (26)
по уравнению (25) выразим i2
через i1 (26)
i2= -![]() - R1*C*
- R1*C*![]() (27)
(27)
i1= i2+
i3=-![]() - (R1*C+
- (R1*C+![]() )*
)*![]() -
-![]() +
+![]() (28) по уравнению (22) выражаем
i1 получаем
дифференциальное уравнение 2-го порядка
(28) по уравнению (22) выражаем
i1 получаем
дифференциальное уравнение 2-го порядка
![]() + (R1*C+
+ (R1*C+![]() )*
)*![]() +
+![]() =
=![]() (29)
(29)
![]() +
+ ![]() *
*![]() +
+![]() =
=![]() (30)
(30)
![]() 6.Составление дифференциального уравнения по методу
6.Составление дифференциального уравнения по методу
D-алгебризации
Обозначим операцию дифференцирования буквой D
Тогда операция интеграла будет 1/D
Из системы уравнений (22-24)
i1= i2+ i3 (31)
L*![]() + i1*R1+
i3*R2=E (32)
+ i1*R1+
i3*R2=E (32)
i3*R2-(Uc(0)+![]() )=0 (33)
)=0 (33)
![]()
![]() i2= i1-i3 (34)
i2= i1-i3 (34)
L*![]() + i1*R1+
i3*R2=E (35) (L*
+ i1*R1+
i3*R2=E (35) (L*![]() + R1)*i1+
i3*R2=E (37)
+ R1)*i1+
i3*R2=E (37)
![]() i3*R2-Uc(0)-
i3*R2-Uc(0)-![]() *( i1-i3)=0
(36) -
*( i1-i3)=0
(36) -![]() *i1+(R2+
*i1+(R2+![]() )*i3= Uc(0)
(38)
)*i3= Uc(0)
(38)
с помощью знаний векторной алгебры решаем систему уравнений
(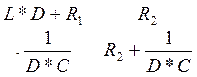 )*(
)*(![]() )=(
)=(![]() ) (39)
) (39)
найдем определитель первой матрицы
Δ=(![]() )(
)(![]() )+
)+![]() =R2*L*D+
=R2*L*D+![]() +R1*R2+
+R1*R2+![]() (40)
(40)
Δi1=E*R2+![]() -R2*Uc(0) (41)
-R2*Uc(0) (41)
i1=![]() =
=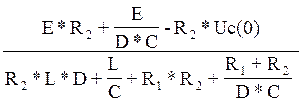 (42)
(42)
i1*( ![]() )=
)= ![]() (43)
(43)
i1*![]() )=
)= ![]() (44)
(44)
i1*![]() )=
)=![]() (45)
(45)
выражаем i1 получаем дифференциальное уравнение 2-го порядка
![]() +
+ ![]() *
*![]() +
+![]() =
=![]() (46)
(46)
7.Анализ полученного уравнения
![]()
1) ![]() т к приложенная
составляющая постоянна
т к приложенная
составляющая постоянна
то производная ее равна 0
получаем ![]() (47)
(47)
2) 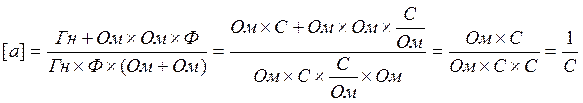 (48)
(48)
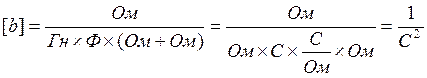 (49)
(49)
8.Решение дифференциального уравнения классическим методом
Записываем наше дифференциальное уравнение
![]() +
+ ![]() *
*![]() +=
+=![]() (50)
(50)
будем искать свободную составляющую в виде
i1св=A1*![]() + A2*
+ A2*![]() (51)
(51)
i1пр=![]() (52)
(52)
ищем полный ток в первой ветви в виде
i1=i1св+i1пр=
A1*![]() + A2*
+ A2*![]() +
+![]() (53)
(53)
i1(0)= ![]() (54)
(54)
при t=0
![]() = A1+ A2+
= A1+ A2+![]() à A1=-
à A1=-![]() - A2 (55)
- A2 (55)
i1= -(![]() + A2)*
+ A2)*![]() + A2*
+ A2*![]() +
+![]() (56)
(56)
при t=0
![]() = -
= -![]() *(
*(![]() + A2)+
+ A2)+![]() *A2=0 A2=
*A2=0 A2=![]() *
*![]()
(57)
A1= -![]() *
*![]()
(58)
i1=![]() -
-![]() *
*![]() *
*![]() +
+![]() *
*![]() *
*![]()
(59)
После вычислений получим
A1=-0.0 627
A2=0.0250
i1=0.1077 -0.0627*![]() +0.0250*
+0.0250*![]()
(60)
9.Определение остальных токов и напряжений
i3= ![]() -
- ![]() -
- ![]() по уравнению (26)
по уравнению (26)
i3=![]() +
+![]() *
*![]() *(
*(![]() )*
)*![]() -
-![]() * *
* *![]() *(
*(![]() )*
)*![]() (61)
(61)
по уравнению (22)
i1= i2+ i3 à i2 =i1- i3
i2= -![]() *
*![]() *(
*(![]() +1)*
+1)*![]() +
+![]() * *
* *![]() *(
*(![]() +1)*
+1)*![]() (62)
(62)
uR1=i1*R1=
R1[![]() -
-![]() *
*![]() *
*![]() +
+![]() * *
* *![]() *
*![]() ] (63)
] (63)
uC=uR2=i3*R2=R2[![]() +
+![]() *
*![]() *(
*(![]() )*
)*![]() -
-![]() *
*![]() *(
*(![]() )*
)*![]() ] (64)
] (64)
uL=L![]() =L*[-
=L*[-![]() *
*![]() *
*![]() +
+![]() * *
* *![]() *
*![]() ] (65)
] (65)
10.Таблица токов и напряжений
|
Уравнение |
t<0 |
t=0 |
t |
|||
|
По з.К. |
По уравн. |
Прин. Режим |
По уравн. |
|||
|
i1 |
0.1077-0.0627* |
|
0.07 |
0.07 |
=0.1077 |
0.1077 |
|
i2 |
-0.0898* * |
0 |
-0,0612 |
-0.0612 |
0 |
0 |
|
i3 |
0.1077+0.027* |
|
0,1312 |
0.1312 |
|
0.1077 |
|
uR1 |
53.85-31.35* |
|
35 |
35 |
|
53.85 |
|
uC |
86.16+21.6* |
|
105 |
105 |
|
86.16 |
|
uR2 |
|
|||||
|
uL |
9.586* |
0 |
0 |
0 |
0 |
0 |
11. Решение полученного ДУ операторным методом:
представим исходную схему по операторному методу
|
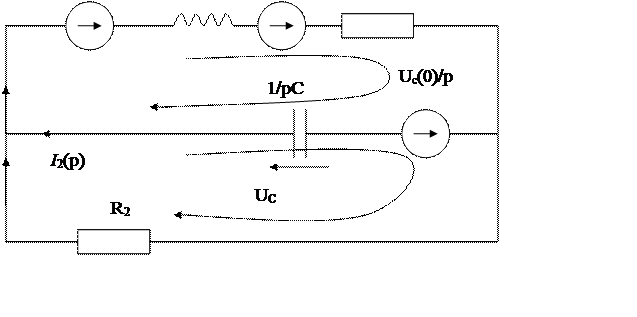 E/p
pL R1
E/p
pL R1
|
|||
|
|||
По законам коммутации
I1(0_)=0.095 A=I1(0)
UC(0_)=142.5 B =UC(0)
Составим систему уравнений по законам Кирхгофа по Операторному методу
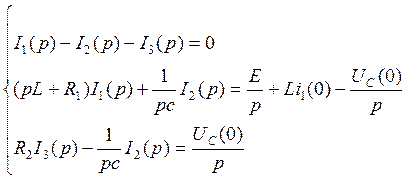 (66)
(66)
из Первого уравнения системы
![]() (67)
(67)
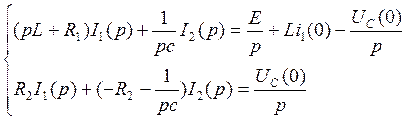
(68)
Получим определитель и решим систему с помощью определительного метода относительно тока в первой ветви
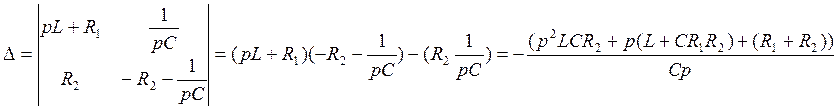
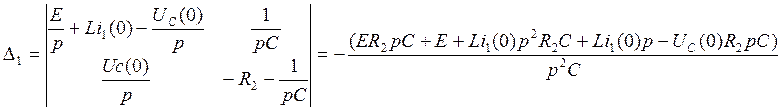
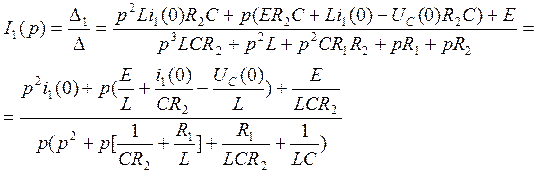
запишем с помощью коэффициентов
 (69)
(69)
![]()
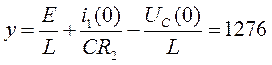 (70)
(70)
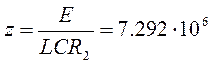 (71)
(71)
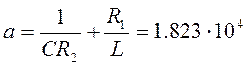 (72)
(72)
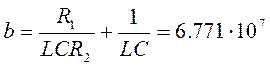 (73)
(73)
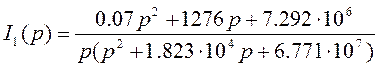 (74)
(74)
знаменатель будет равен 0 при
p1=0 p2= -5194 ![]() p3= -13040
p3= -13040![]()
производная Функции знаменателя
![]()
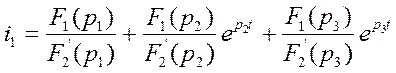 (75)
(75)
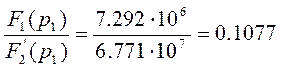
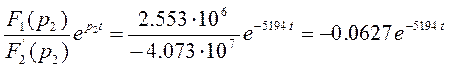
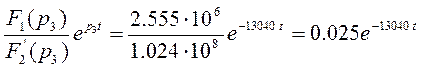
Получим конечное выражение для тока
![]() (76)
(76)
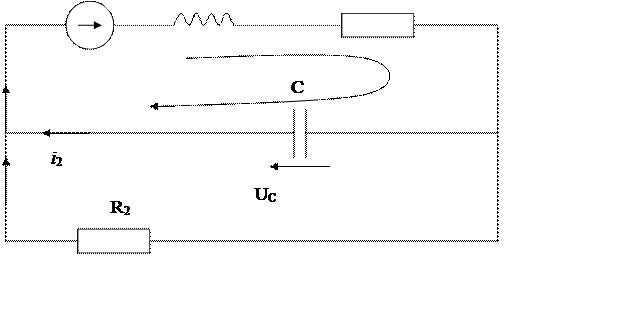
12. Расчёт п.п. методом ПС:
|
|
Стрелка указывает направление обхода контура
Составим систему уравнений по законам Кирхгофа и Ома
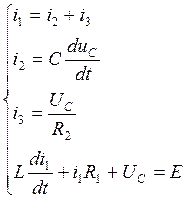 (77)
(77)
Выразим из него производную тока в ветви 1 по времени
![]() (78)
(78)
получим для тока выражение
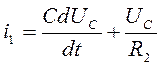
производная напряжения на конденсаторе
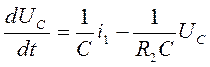 (79)
(79)
Квадратнаяматрица собственных коэффициентов системы, которые определяются структурой цепи и параметрами элементов.
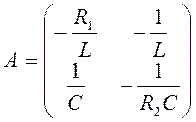 =(
=(![]() )
)
Вектор независимых переменных, элементы которого определяются входными воздействиями.
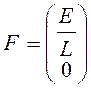 =(
=(![]() )
)
Вектор начальных условий.
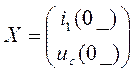 =(
=(![]() )
)
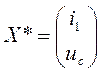
dX - описывает правую часть уравнений, разрешенных относительно первых производных
dX*=A * X* + B * F (80)
![]()
постоянные времени переходного процесса
![]()
![]()
Время переходного процесса
![]()
13.Расчет переходных процессов, составленных методом переменных состояния с помощью программы MathCad.
Вектор независимых переменных, элементы которого определяются входными воздействиями.
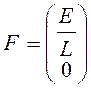 =(
=(![]() )
)
Вектор начальных условий.
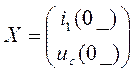 =(
=(![]() )
)
D - описывает правую часть уравнений, разрешенных относительно первых производных
![]()
Начальный момент переходного процесса
![]()
Конечный момент переходного процесса
![]()
Число шагов для численных расчетов.
![]()
Применение метода Рунге-Кутта. Решение Z представляет собой матрицу размера
Nx3.
Первый столбец этой матрицы Z<0> содержит моменты времени, столбец Z<1> содержит значения тока, а столбец Z<2> содержит значения функции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.