Курсовая работа
Расчет переходных процессов
Студент: Ставинов П.А.
Группа: Н-132
Преподаватель: Тораманян О.С.
Санкт-Петербург 2005г
Содержание
1 Исходные данные
![]()
2 Решение задачи классическим методом
![]()
3 Решение задачи операторным методом
![]()
4 Составление систем уравнений методом переменных
состояния![]()
5 Построение графиков и проверка результатов
![]()
1 Исходные данные
 В схеме,
изображенной на рис.1, рубильник Р в момент времени t=0
замыкается (происходит коммутация). Задана ЭДС постоянного источника
Е=80 В, а также сопротивления R1=200 Ом и R2=30 Ом, индуктивность L=0.09 Гн и
емкость С=4 мкФ.
В схеме,
изображенной на рис.1, рубильник Р в момент времени t=0
замыкается (происходит коммутация). Задана ЭДС постоянного источника
Е=80 В, а также сопротивления R1=200 Ом и R2=30 Ом, индуктивность L=0.09 Гн и
емкость С=4 мкФ.
Требуется найти:
× Законы изменения токов i1(t), i2(t), i3(t) и напряжений ur1(t), ur2(t), uc(t), ul(t). Решить задачу классическим и операторным методами.
× Составить математическую модель переходного процесса по методу переменных состояния и подготовить полученную систему дифференциальных уравнений для расчета на ЭВМ.
× Построить временные диаграммы токов i1(t), i2(t), i3(t) и напряжений ul(t), uc(t), ur1(t), ur2(t).
× Проверить результат.
2 Решение задачи классическим методом
Для нахождения законов изменения токов и напряжений необходимо знать полное напряжение, которое имеет вид:
![]()
Т.к. Е=const, принужденная составляющая напряжения также не зависит от времени.
2.1 Составление системы дифференциальных уравнений по законам Кирхгоффа

Запишем систему уравнений (1.1) для момента времени после коммутации. Количество уравнений в системе должно быть равно числу неизвестных токов. Уравнение (2) составим по первому закону Кирхгоффа, (3) и (4) – по второму закону Кирхгоффа.
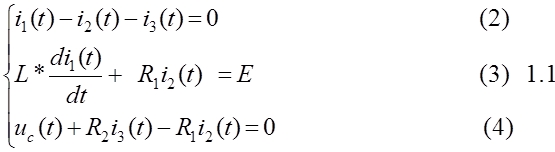
Уравнение связи для конденсатора:

2.2 Нахождение дифференциального уравнения относительно величины uc(t)
Степень дифференциального и характеристических уравнений относительно uc(t) равна числу независимых начальных условий (ННУ) в схеме, т.е. порядок равен 2.
Из уравнения (4)

Из уравнения (2)
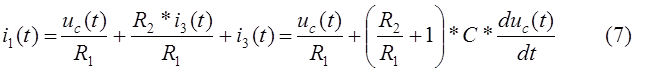
Подставляем в (3)
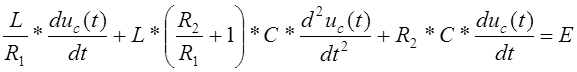
Преобразуем
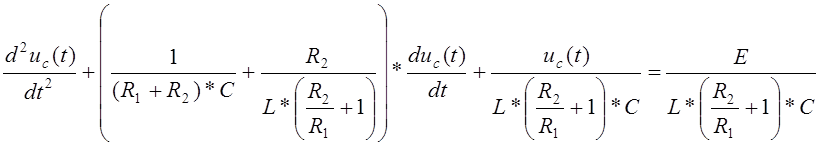
![]()
2.2.1 Составление характеристического уравнения по
дифференциальному уравнению.
Для получения однородного дифференциального уравнения нужно в (8) правую часть тождественно приравнять 0.
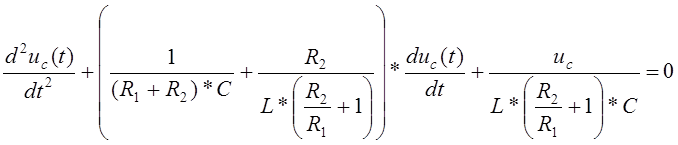
Заменяем d2uc/dt2, duc/dt, uc на a2, a, 1 соответственно.
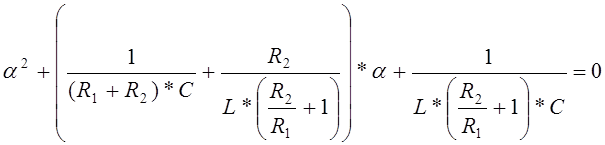
![]()
2.3 Нахождение дифференциального уравнения
относительно величины il(t)
Выразим из системы 1.1 i1(t)
Для этого из (4) выразим uc(t), а потом из uc(t) выразим i3(t).
![]()
![]()
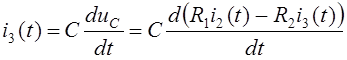
Выразим из (3) ток i2(t)
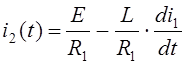
Подставляем полученные величины в (2)
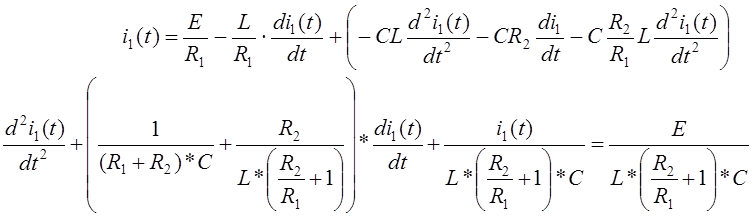 |
|||
Преобразовав, получаем
Заметим, что полученное линейное неоднородное дифференциальное уравнение для тока на катушке имеет идентичное характеристическое уравнение с уравнением (8)
2.4 Определение характеристического
уравнения по входному сопротивлению цепи.
При реализации данного метода необходимо найти входное сопротивление цепи.
Для начала найдем сопротивление параллельного участка цепи:
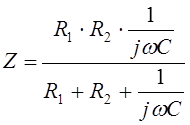 |
|||
Теперь находим полное сопротивление цепи
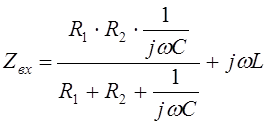
![]()
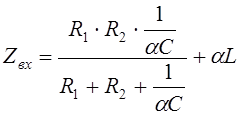
![]() Заменяем jw на
Заменяем jw на
![]()
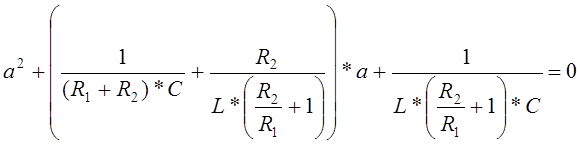 Полученное выражение приравниваем к нулю и
преобразовываем
Полученное выражение приравниваем к нулю и
преобразовываем
2.5 Нахождение характеристического уравнения методом
D-алгебраизации.
Перепишем
(1.1) с учетом 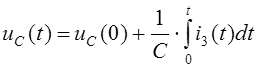
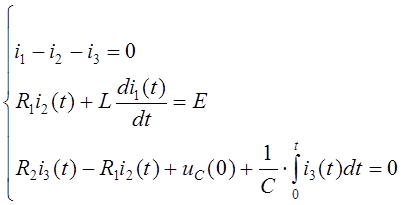
Сделаем замену
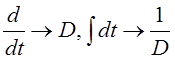

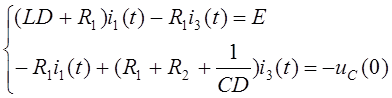
i1(t) можно найти по формуле Крамера:
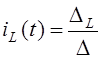 где
где
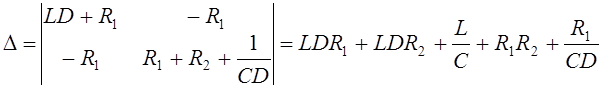
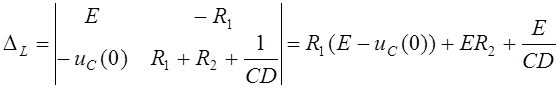
Подставим определители в формулу Крамера
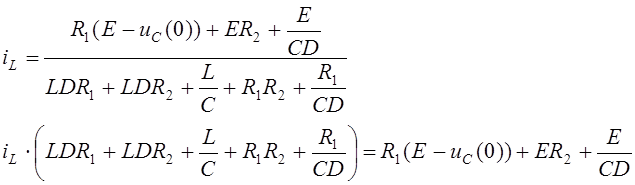
Приравняв правую часть к нулю, получим характеристическое уравнение
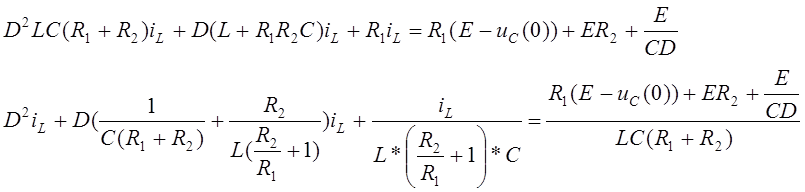
Сделаем обратную замену 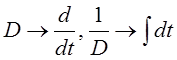 и приравняв правую
часть к нулю, получим линейное однородное дифференциальное уравнение.
и приравняв правую
часть к нулю, получим линейное однородное дифференциальное уравнение.
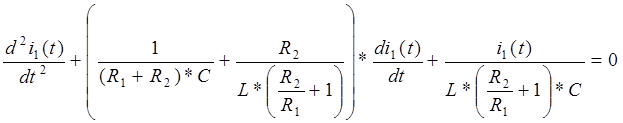
Заметим, что данное уравнение имеет характеристическое уравнение, идентичное (9).
2.6 Определение корней характеристического уравнения.
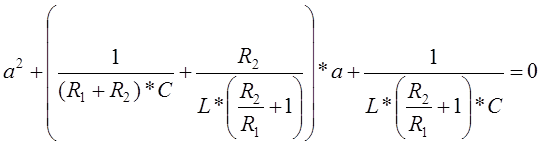
Произведем замену
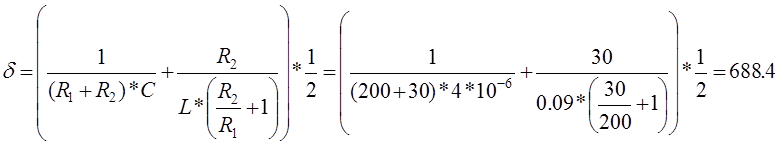
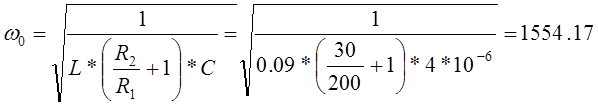
Проверим размерность полученных корней
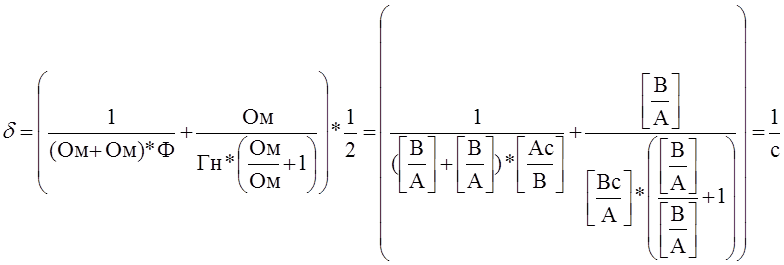
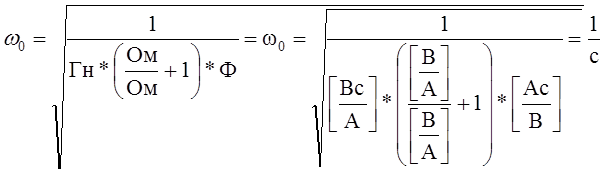
Уравнение (16) с учетом замены приобретает вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.