Нахождение законов изменения токов и напряжений. Составление системы дифференциальных уравнений по законам Кирхгоффа, страница 3

3.7 Нахождение оригинала функции i_L(t)

Знаменатель уравнения (42) полностью совпадает со знаменателем уравнения (37). Следовательно, и корни будут одинаковыми.

 

Дальше действуем по теореме разложения (40)

  

      

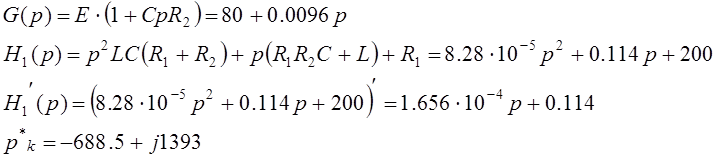
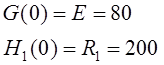
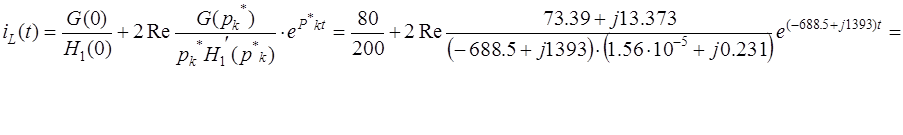
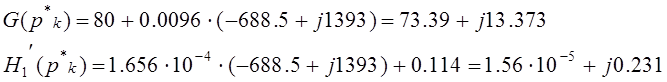
Учитывая, что  и      

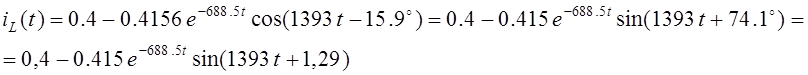
Данное уравнение полностью совпадает с величиной, найденной в пункте 2.11 классическим методом.

4 Составление систем уравнений по методу

переменных состояния.

Переменные состояния – величины, определяющие энергетическое состояние цепи, т.е. i_L(t) и u_C(t).

4.1 Составление системы по законам Кирхгоффа.

Записываем систему 1.1

                  

                                           

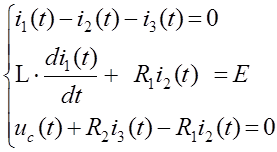
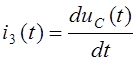
4.2 Преобразование полученной системы в систему уравнений в форме

Коши относительно производных переменных состояния.

Подставляем (45) и (43) в (44)

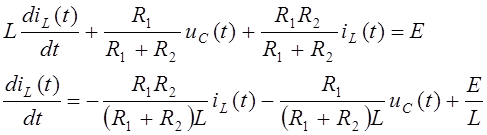
Подставляем (43) в (45) с учетом (46)

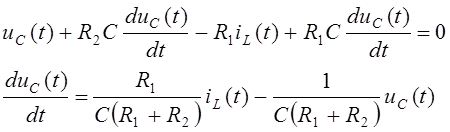
Уравнения (47) и (48) запишем в форме Коши:

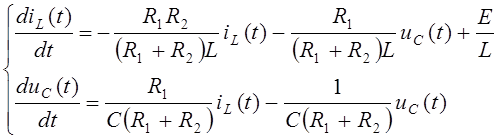
Принимаем

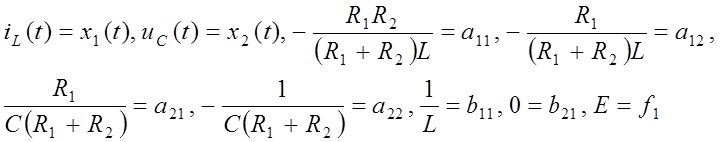
Получаем систему уравнений в форме Коши

                         

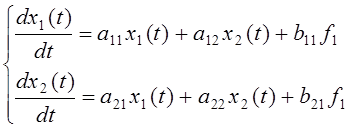
Из системы 3.0 запишем матрицу коэффициентов, стоящих перед x₁(t), x₂(t), порядка , где n – количество переменных состояния.

 

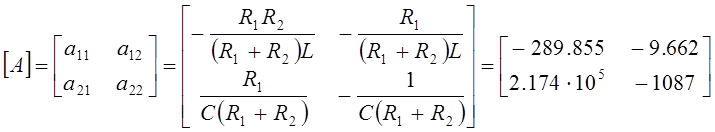
Матрица  содержит в себе все пассивные элементы цепи.

Из системы 3.0 запишем матрицу коэффициентов, стоящих перед Е порядка , m - количество источников.

                                               

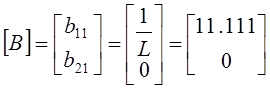
ННУ (23) и (24) объединим в систему

                                                                    

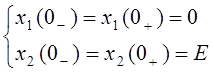
По 3.1 запишем матрицу-столбец начальных условий порядка n.

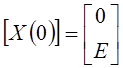                                                                           (51)

Из 3.0 получим матрицу-столбец входных воздействий порядка m.

                                                                    (52)

С учетом (49), (50), (52) приведем систему 3.0 к виду:

,                                                    

где  - дифференциал матрицы искомых величин.

Объединим (53) и (51) в матричную систему

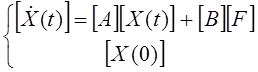                                                          3.2

4.3 Нахождение переменных состояния.

Решение системы 3.2 имеет вид

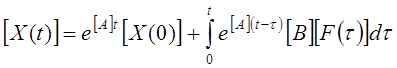                                      (54)

Первое слагаемое описывает свободные процессы в системе, второе – принужденные при нулевом исходном состоянии.

, где  - собственные числа матрицы , которые находятся как корни уравнения

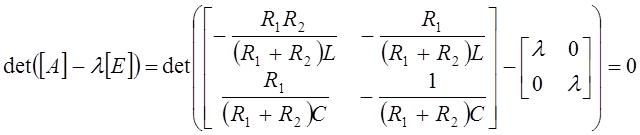
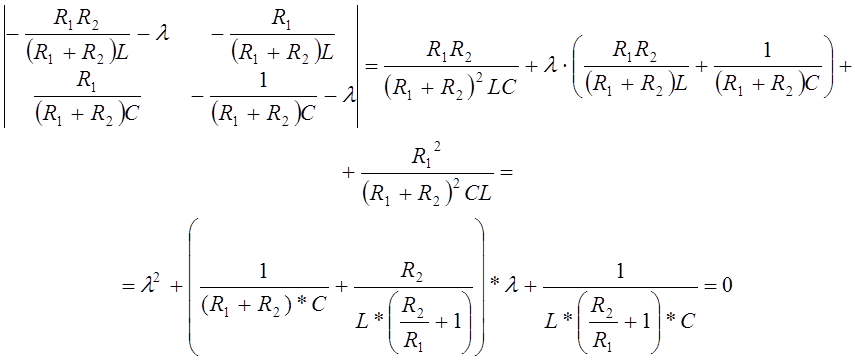
Получили характеристическое уравнение, идентичное (9).

5 Построение графиков и проверка результатов

5.1 Построение графиков

На практике переходный процесс заканчивается спустя  

где Т – период колебаний переходного процесса, равный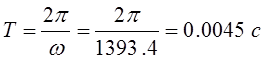

Поэтому время переходного процесса

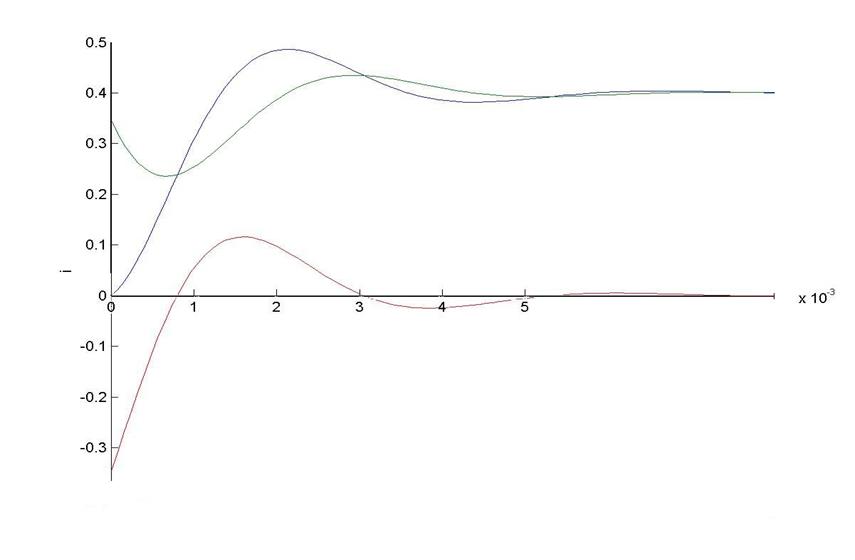На графике 1 можно в любой момент времени проверить соблюдение первого закона Кирхгоффа – первый ток равен сумме второго и третьего.

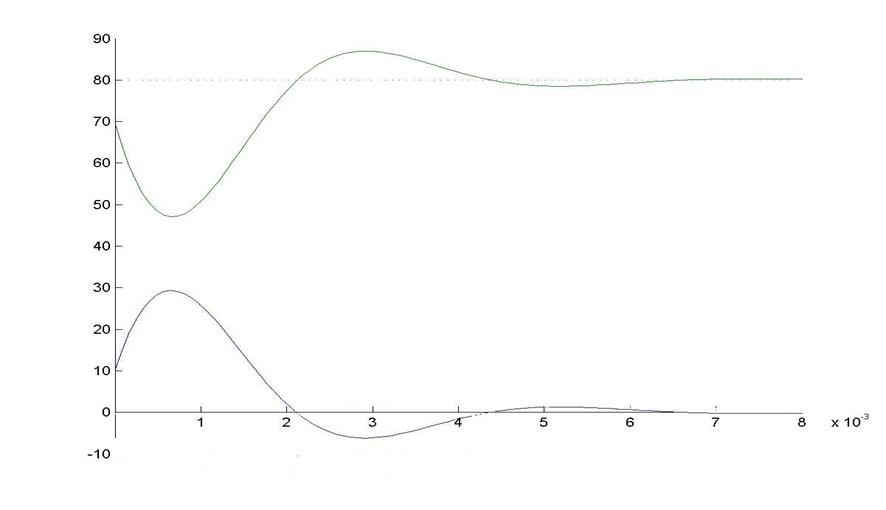
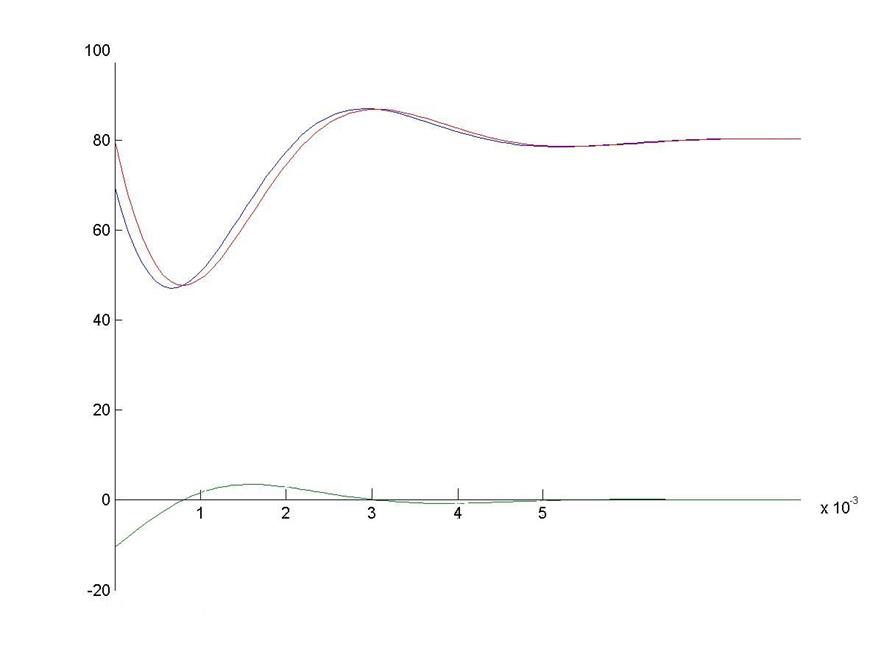
5.2 Проверка токов и напряжений в заданные моменты времени

	t=0	t=0.001	t=0.003	t=0.004	t=0.005	t=0.0065
i1(t)	0.00029	0.3076	0.4383	0.3855	0.3878	0.4038
i2(t)	0.3479	0.2539	0.4346	0.4094	0.3929	0.3994
i3(t)	-0.3474	0.0545	0.0035	-0.0239	-0.0051	0.0044

                                                                                                             

	t=0	t=0.001	t=0.003	t=0.004	t=0.005	t=0.0065
uL(t)	10.1917	25.7655	-6.1489	-1.5940	1.2693	0.0976
uR1(t)	69.5841	50.7717	86.9240	81.8722	78.5844	79.8763
uR2(t)	-10.4206	1.6343	0.1052	-0.7182	-0.1539	0.1320
uC(t)	80	49.1435	86.8177	82.5896	78.7385	79.7444
E	80	80	80	80	80	80

Все графики построены и расчеты произведены в системе MatLab 6.5.