Решение уравнения (17) будет иметь комплексно-сопряженные корни, т.к.
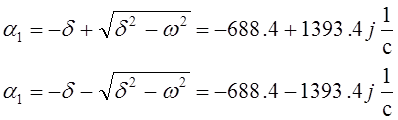
![]()
2.7 Запись свободной составляющей uc
Выражение свободной составляющей напряжения определяется видом корней характеристического уравнения (17). Т.к. корни комплексно-сопряженные, выражение свободного напряжения имеет вид:
![]()
![]()
2.8 Расчет принужденной составляющей uc
В схеме, изображенной на рисунке 2, закоротим индуктивность и разорвем ветвь с емкостью. Теперь все токи не зависят от времени.

По второму закону Кирхгоффа напряжение на конденсаторе равно:
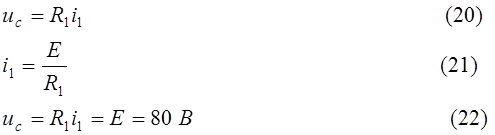
Такой же результат мы получим, если в уравнении (8) учтем, что производная от константы равна нулю (принужденная составляющая uc не является функцией времени).
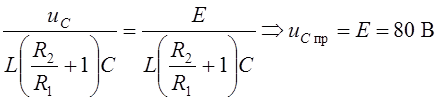
2.9 Расчет начальных независимых и зависимых условий при t=0+
Независимые начальные условия – ток на индуктивности il(0-) и напряжение на конденсаторе uc(0-) до коммутации.
До коммутации ток в цепи не шел => il(0-)=0
Используя первый закон коммутации, получаем:
![]()
![]()
По второму закону Кирхгоффа в момент времени до коммутации uc(o-)=E
Используя второй закон коммутации, получаем:
![]()
![]()
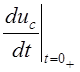 Для определения
постоянных интегрирования А1 и Q необходимо знать зависимые начальные условия, т.е.
Для определения
постоянных интегрирования А1 и Q необходимо знать зависимые начальные условия, т.е.
Выразим из уравнения (7).
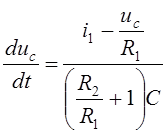
Подставим момент времени t=0 и независимые начальные условия:
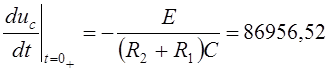
![]()
2.10 Запись полного решения uc(t) и определение постоянных
интегрирования.
Из выражения () при t=0
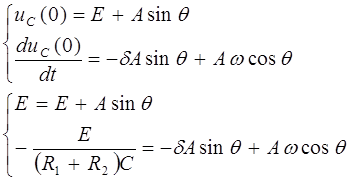 |
|||
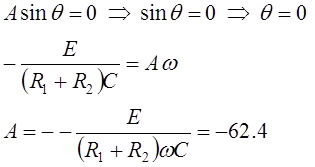
![]()
 |
2.11 Определение токов и напряжений в схеме
Подставим в выражение () численные значения ЭДС, корней характеристического уравнения и постоянных интегрирования.
![]()
Третий ток мы найдем из уравнения (5), учитывая 

Второй ток находим из (6)
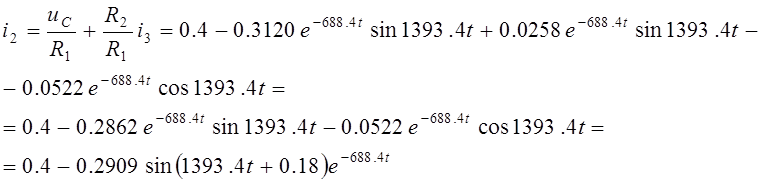
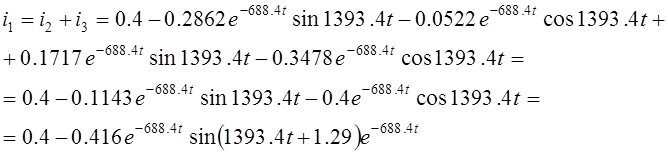 Первый ток найдем
по первому закону Кирхгоффа
Первый ток найдем
по первому закону Кирхгоффа
Далее находим напряжение на индуктивности
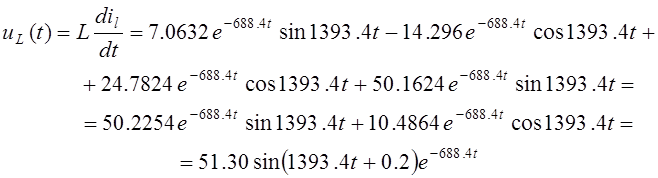
По закону Ома находим напряжения на сопротивлениях

3 Решение задачи операторным методом
Операторный метод решения линейных дифференциальных уравнений часто применяется при расчете электрических цепей. В основу этого метода положены преобразования Лапласа, суть которых состоит в замене функции вещественного переменного f(t), называемой оригиналом, соответствующей ей функцией F(p) комплексного переменного p, называемой изображением.
 Оригинал и изображение связаны соотношением, называемым прямым
преобразованием Лапласа.
Оригинал и изображение связаны соотношением, называемым прямым
преобразованием Лапласа.
3.1 Определение начальных условий схемы при t=0+
Выпишем найденные в пункте 2.9 независимые начальные условия
![]()
![]()
![]()
3.2 Составление операторной схемы замещения
 В схему изображений при ненулевых начальных условиях последовательно
с индуктивностью включается источник ЭДС, сонаправленный с током на катушке, а
последовательно с емкостью – дополнительный источник ЭДС, направленный
противоположно положительному направлению тока в ветви.
В схему изображений при ненулевых начальных условиях последовательно
с индуктивностью включается источник ЭДС, сонаправленный с током на катушке, а
последовательно с емкостью – дополнительный источник ЭДС, направленный
противоположно положительному направлению тока в ветви.
3.3 Составление системы алгебраических уравнений в операторном виде
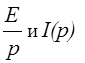
![]()
![]()
![]()

![]() Для записи
операторных сопротивлений заменяем jw на p, E и i(t) будем рассматривать как функции оригиналы, имеющие изображения
Для записи
операторных сопротивлений заменяем jw на p, E и i(t) будем рассматривать как функции оригиналы, имеющие изображения
3.4 Нахождение операторного изображения искомой величины UC(p)
Найдем из системы 2.8 изображение UC(p)
![]()
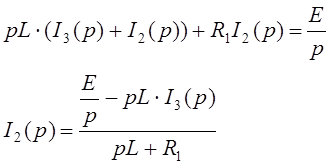 Подставляем (29) в (30), учитывая (28)
Подставляем (29) в (30), учитывая (28)
![]()
![]()
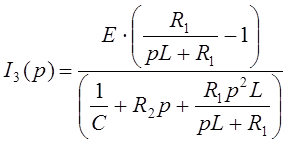 Подставляем (34) в (31) и выражаем третий ток
Подставляем (34) в (31) и выражаем третий ток
Подставляем (35) в (32)
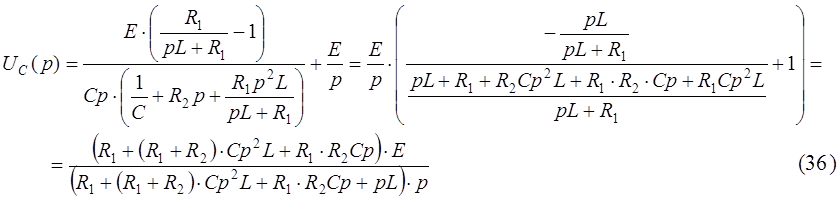 |
3.5 Нахождение оригинала искомой функции uC(t)

![]()
![]()
![]() Приравняем
к нулю знаменатель и найдем корни:
Приравняем
к нулю знаменатель и найдем корни:
![]()
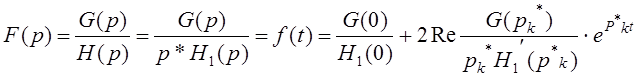 Запишем теорему разложения при наличии
комплексно-сопряженных корней
Запишем теорему разложения при наличии
комплексно-сопряженных корней
![]()
![]()
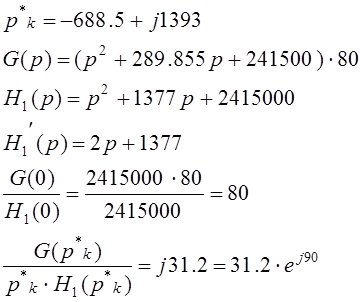 В нашем случае:
В нашем случае:
![]()
 Подставим значения и выпишем
результат
Подставим значения и выпишем
результат
Оригинал напряжения полностью совпадает с уравнением напряжения на конденсаторе, найденным классическим методом в пункте 2.11
3.6 Нахождение изображения величины iL(t)
Из системы 2.7 найдем изображение искомого тока.
Из (30) и (31)

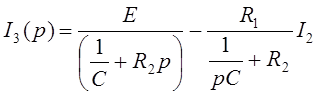
Подставляем в (29) и находим:
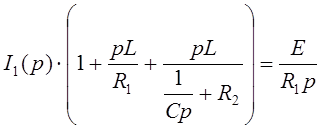
Преобразив, получим:
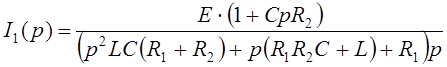 (42)
(42)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.