Законы изменения токов. Расчёт переходного процесса классическим методом. Временная диаграмма напряжений, страница 2

= 0.111 – 0.07e^-12077t + 0.04e^-20701t  А.

Для заданной схемы: u_L = u_с – R₃i₃ , тогда

u_L = 33.3 – 11.9е^-12077t + 3.6e ^–20701t – 33.3 + 21e^-12077t - 12e^-20701t В.

8.  Расчитаем и построим временные диаграмы.

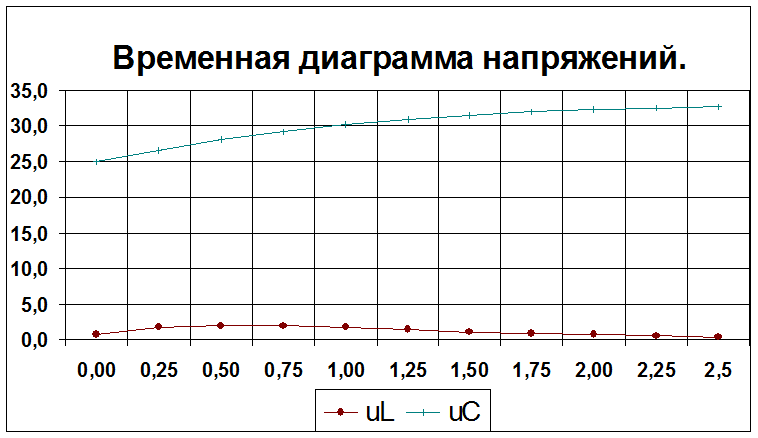
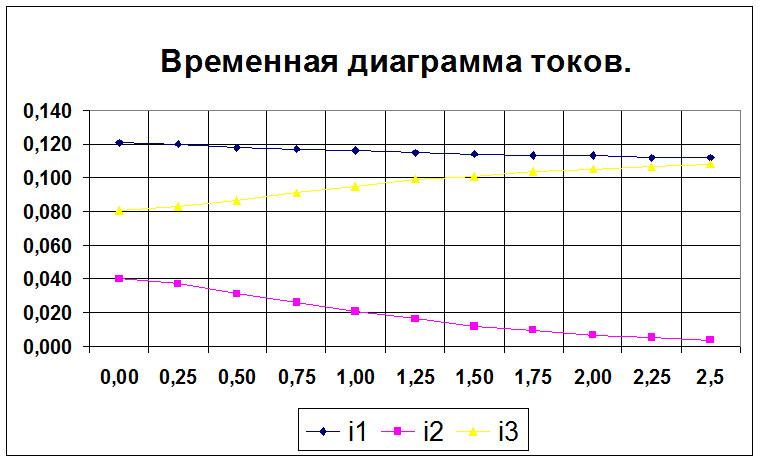
Рассмотрим промежуток времени 3t_мах =    = » 2.5*10^-4 c.

Рассчитаем значение найденных величин на этом промежутке.

Величины	0,00	0,25	0,50	0,75	1,00	1,25	1,50	1,75	2,00	2,25	2,5
	*10-4 c
i1	0,121	0,120	0,118	0,117	0,116	0,115	0,114	0,113	0,113	0,112	0,112
i2	0,040	0,037	0,031	0,026	0,021	0,016	0,012	0,010	0,007	0,005	0,004
i3	0,081	0,083	0,087	0,091	0,095	0,099	0,101	0,104	0,105	0,107	0,108
uL	0,7	1,7	2,0	1,9	1,7	1,4	1,1	0,9	0,7	0,5	0,4
uC	25,0	26,6	28,1	29,2	30,2	30,9	31,5	32,0	32,3	32,5	32,7

Расчёт переходного процесса операторным методом.

1.    Построим операторную схему замещения.

2.    Для полученной операторной схемы замещения составим систему уравнений по первому и второму законам Кирхгофа в операторной форме.

I₁(p) - I₂(p) - I₃(p) = 0,

R₁I₁(p) + I₂(p) = - ,

- I₂(p) + (R₃ + pL)I₃(p) = + Li₃(0) ,                          (**)

I₂(p) = C( pU_c(p) – u_c(0) ).

3.  Разрешим полученную систему относительно изображения искомой переменной U_c(p).

Из системы (**) выразим токи I₁(p) и I₃(p) относительно изображения искомой переменной.

I₁(p) = - = = = - ,

I₃(p) = + + = + =

= + .

Подставим полученные выражения в первое уравнение системы (**).

- - CpU_c(p) + Сu_c(0) - - = 0 ,

-U_c(p) ( + CP + ) + + Сu_c(0) - = 0 ,

U_c(p) = ,

U_c(p) = ,

U_c(p) = ,

U_c(p) = ,

U_c(p) = .

4.  По теореме разложения найдём оригинал-закон изменения u_c(t).

Приравняем знаменатель 0 и найдём его корни.

p₁ = 0,

p₂ = -12077,

p₃ = -20701.

U_c(p) º u_c(t) = S e^pkt , где

G(p) =  ,

H¹(p) = 3p² + + = .

Тогда

u_c(t) = e^{P t} +

+ e^{P t} +

+ e^{P t}.

Подставим числовые значения.

u_c(t) = + e^-12077t +

+ e^-20701t =

= 33.3 – 11.9e^-12077t + 3.6e^-20701t.

5.    Разрешим систему (**) относительно изображения искомой переменной I_L(p).

Из системы (**) выразим токи I₁(p) и I₂(p) относительно изображения искомой переменной I₃(p) = I_L(p).

I₁(p) = + ,

I₂(p) = (R₃ + pL)pCI₃(p) - u_c(0)C - LpCi₃(0) , тогда   I₁(p) = - + + = - + .

Подставим полученные уравнения в первое уравнение системы (**).

- + - (R₃ + pL)pCI₃(p) + u_c(0)C + LpCi₃(0) - I₃(p) = 0,

I₃(p) = ,

I₃(p) = ,

I₃(p) = .

6.  По теореме разложения найдём оригинал-закон изменения i₃(t).

Приравняем знаменатель 0 и найдём его корни.

p₁ = 0,

p₂ = -12077,

p₃ = -20701.

I₃(p) º i₃(t) = S e^pkt , где

G(p) =  ,

H¹(p) = 3p² + + = .

Тогда

i₃(t) = e^{P t} +

+ e^{P t} +

+ e^{P t} .

Подставим числовые значения.

i₃(t) = + e^-12077t +

+ e^-20701t =

= 0.11 – 0.07e^-12077t + 0.04e^-20701t.

Подготовка системы дифференциальных уравнений, составленных по методу переменных состояний, для расчёта на ЦВМ.

Составим систему дифференциальных уравнений в форме Коши.

 

= - i₃ + u_c ,                                            (***)

= - i₃ - u_c + .

Подставив численные значения в уравнение системы (***) и системы уравнений (6) получим:

= -3*10⁴i₃ + 10²u_c ,

= -1.7*10⁶i₃ – 2.8*10³u_c + 2.8*10⁵ ,

i₃(0) = 0.083 А,

u_c(0) = 25 В.

 

=>                      -3*10⁴            10²

A =

-1.7*10⁶      - 2.8*10³

 

0

B =

2.8*10⁵

 

0.083

Y(0) =

25

E = 100 В.