Дано:
 |
![]()
![]()
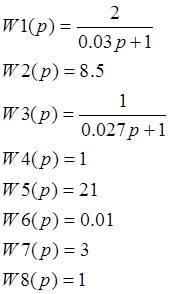
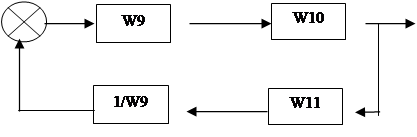
1. Упростим и преобразуем структурную схему т.о., чтобы получить передаточную функцию замкнутой и разомкнутой системы.
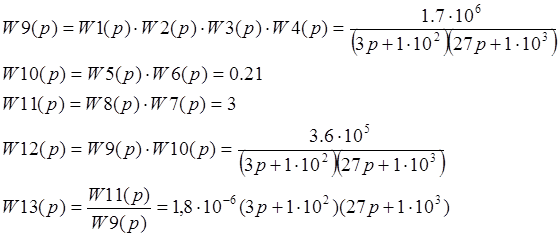
 |
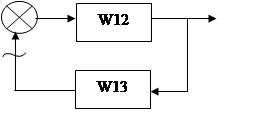
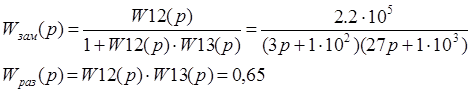
2. Определим устойчивость системы по критерию Ляпунова.
Для устойчивости замкнутой системы необходимо и достаточно, чтобы действительные части корней характеристического уравнения замкнутой системы были меньше нуля.
![]()
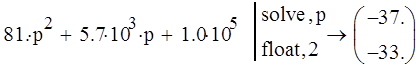
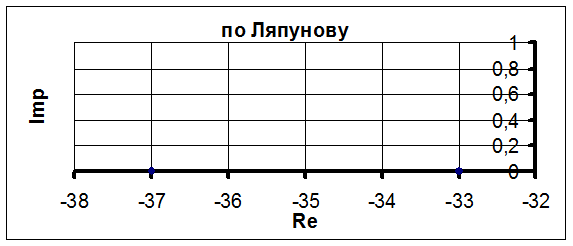
Вывод: по критерию Ляпунова данная система является устойчивой.
3. Определим устойчивость системы по критерию Найквиста.
Для построения годографа Найквиста в
характеристическом полиноме замкнутой системы р заменяем на ![]() . Выделим
действительную и мнимую часть и построим их зависимость.
. Выделим
действительную и мнимую часть и построим их зависимость.
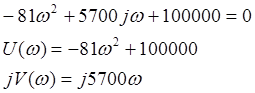
|
0 |
10 |
20 |
40 |
60 |
80 |
100 |
200 |
300 |
|
100000 |
91900 |
67600 |
-29600 |
-191600 |
-418400 |
-710000 |
-3140000 |
-7190000 |
|
0 |
57000 |
114000 |
228000 |
342000 |
456000 |
510000 |
1140000 |
1710000 |
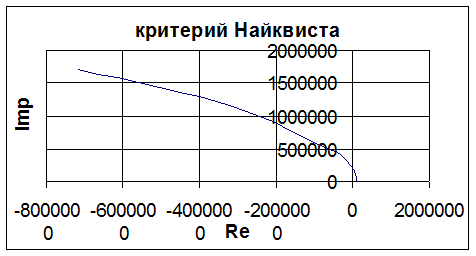
Вывод: годограф Найквиста, построенный для замкнутой системы, не охватывает начала координат, т.е. на отрезке от - ∞ до –1 по действительной оси годограф не имеет пересечений с данной осью, следовательно, при устойчивой разомкнутой системе, замкнутая система устойчива.
4. Определим область наибольшей устойчивости с помощью Д - разбиения.
Для построения области,
подозрительной на устойчивость, необходимо в характеристическом уравнении
выразить коэффициент ![]() ,
выражение с другой стороны от знака «=» приравнять к 0, р заменить на
,
выражение с другой стороны от знака «=» приравнять к 0, р заменить на ![]() и выделить
действительную и мнимую часть.
и выделить
действительную и мнимую часть.
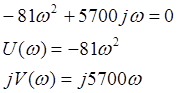
|
w |
-100 |
-60 |
-40 |
-30 |
-20 |
-10 |
10 |
20 |
30 |
40 |
60 |
100 |
|
U(w) |
-8,10E+05 |
-2,92E+05 |
-1,30E+05 |
-7,29E+04 |
-3,24E+04 |
-8,10E+03 |
-8,10E+03 |
-3,24E+04 |
-7,29E+04 |
-1,30E+05 |
-2,92E+05 |
-8,10E+05 |
|
jV(w) |
-5,70E+05 |
-3,42E+05 |
-2,28E+05 |
-1,71E+05 |
-1,14E+05 |
-5,70E+04 |
5,70E+04 |
1,14E+05 |
1,71E+05 |
2,28E+05 |
3,42E+05 |
5,70E+05 |

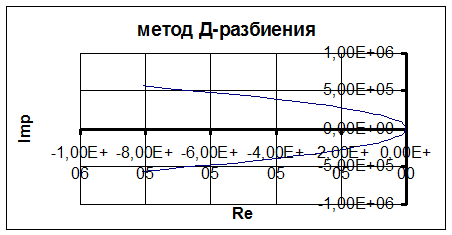
Для определения области наибольшей устойчивости выделяются участки слева направо, выбираются к - корней с отрицательной действительной частью, а затем определяется количество таких корней в других областях, при этом при переходе от заштрихованной к не заштрихованной области к увеличивается, от не заштрихованной к заштрихованной к уменьшается.
Для проверки выбирается некоторое действительное
число из этой области, подставляется вместо ![]() и устойчивость
определяется по любому из известных методов для данного характеристического
уравнения. Возьмем метод Ляпунова
и устойчивость
определяется по любому из известных методов для данного характеристического
уравнения. Возьмем метод Ляпунова ![]() из
области I
из
области I
![]()
следовательно в области I к=1 , возьмем ![]() из области II
из области II
![]()
следовательно в области II к=2
По методу Ляпунова замкнутая система устойчива, следовательно область II - область с наибольшей устойчивостью.
5. Определим показатели качества системы.
Прямые оценки качества:
![]()
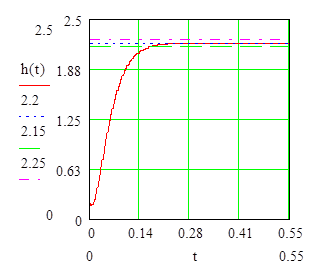
hуст(t)=2.2 – установившееся состояние системы
hуст(t)=2.2∙5%=0.11 – значение 5%-ой трубы
t1=0.21 – время первого согласования
tH=0.21 – время нарастания
tP=0.17 – время регулирования
σ=0 – перерегулирование
6. Косвенные оценки качества:
![]()
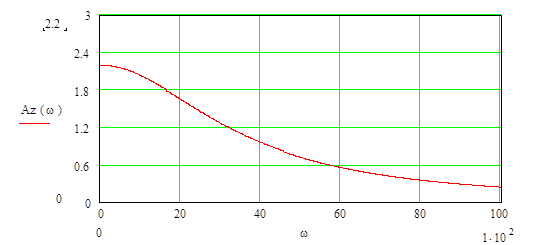
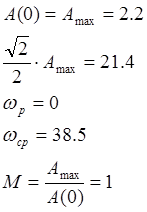
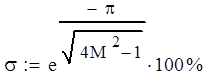
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.