МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ОБЪЕКТОВ ИЛИ СИСТЕМ С ПОМОЩЬЮ ГРАФОВ.
Цель работы: приобрести навыки математического описания САУ с помощью графов, а также оптимизации ориентированных и неориентированных графов и составления матриц смежности и инцидентности.
Граф – это пара множеств X и U, где X – это множество вершин, U – множество дуг их соединяющих.
Например: G={X;U}, где ![]()
Если дуги графа имеют направление, обозначенное стрелками, граф называется ориентированным; если дуги не направленные, то граф – неориентированным.
Различают графы взвешенные и не взвешенные.
Граф называется взвешенным, если каждой его дуге приписывается некоторое значение, называемое весом дуги. Есливес дуги не определен, граф - не взвешенный.
ОРИЕНТИРОВАННЫЕ ГРАФЫ.
Направленный отрезок, соединяющий одну вершину с другой, называется дугой.
 Последовательность дуг, у которых конец предыдущей совпадает с началом,
называется путем.
Последовательность дуг, у которых конец предыдущей совпадает с началом,
называется путем.
Каждому пути можно поставить в соответствии его длину. Длина пути определяется количеством дуг, входящих в этот путь. Длина пути может быть определена суммой весов дуг, входящих в этот путь.
Простой путь – это путь, у которого ни одна из дуг не встречается дважды.
Путь называется элементарным, если ни одна из его вершин не встречается дважды.
Контур – это путь, начало и конец которого совпадают.
Элементарный контур – это контур, у которого все вершины различны.
Петля – это дуга, соединяющая одну и ту же вершину.
НЕОРИЕНТИРОВАННЫЕ ГРАФЫ.
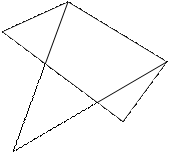 Ребро – это отрезок, соединяющий две вершины.
Ребро – это отрезок, соединяющий две вершины.
Цепь – это последовательность ребер.
Цикл – это цепь, у которой начало и конец совпадают.
Для обоих графов.
Степень вершины – это число ребер или дуг, входящих или выходящих из вершины.
Граф называется связным, если любые его две вершины можно соединить путем или цепью.
Дерево графа – это совокупность ребер или дуг, которые соединяют все вершины графа, но не образуют ни одного цикла или контура.
Величина дерева определяется суммой его ветвей: количеством ребер или
дуг, входящих в него. Если количество вершин обозначить через n,
количество дуг через m, то количество ветвей ![]()
Хорда – это ветвь графа, которую необходимо отбросить, чтобы получить дерево.
Количество хорд в графе определяется как![]()
Ранг графа – это число хорд, входящих в этот граф.
МАТРИЧНОЕ ОПИСАНИЕ ГРАФА.
Две вершины называются смежными, если существует дуга или ребро их соединяющие.
Матрица смежности для неориентированного графа определяется так:
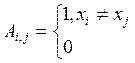
|
А= |
X1 |
X2 |
X3 |
X4 |
X5 |
|
|
X1 |
0 |
1 |
0 |
1 |
0 |
|
|
X2 |
1 |
0 |
1 |
0 |
1 |
|
|
X3 |
0 |
1 |
0 |
1 |
1 |
|
|
X4 |
1 |
0 |
1 |
0 |
0 |
|
|
X5 |
0 |
1 |
1 |
0 |
0 |
Свойства матрицы смежности:
- сумма элементов матрицы смежности в каждой строке равна степени соответствующей вершины.
- матрица смежности является симметричной относительно главной диагонали с нулями на ней.
Для ориентированного графа: единица ставится в том случае если из вершины выходит дуга, если дуга входит то ставится 0.
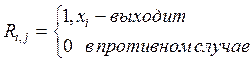
|
R= |
X1 |
X2 |
X3 |
X4 |
X5 |
|
|
X1 |
0 |
1 |
1 |
0 |
1 |
|
|
X2 |
0 |
1 |
1 |
0 |
0 |
|
|
X3 |
0 |
0 |
0 |
1 |
1 |
|
|
X4 |
0 |
1 |
0 |
0 |
0 |
|
|
X5 |
0 |
0 |
0 |
0 |
0 |
Матрица инцидентности. Вершина и дуга называются инцидентными, если дуга касается ее.
Матрица инцидентности для неориентированного графа:
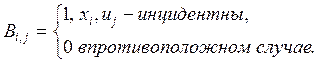
|
B= |
U1 |
U2 |
U3 |
U4 |
U5 |
U6 |
|
|
X1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
X2 |
1 |
1 |
0 |
0 |
1 |
0 |
|
|
X3 |
0 |
1 |
1 |
0 |
0 |
1 |
|
|
X4 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
X5 |
0 |
0 |
0 |
0 |
1 |
1 |
Матрица инцидентности для ориентированного графа:
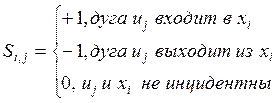
|
S= |
U1 |
U2 |
U3 |
U4 |
U5 |
U6 |
U7 |
U8 |
|
|
X1 |
-1 |
0 |
0 |
0 |
-1 |
0 |
-1 |
0 |
|
|
X2 |
+1 |
-1 |
0 |
+1 |
0 |
0 |
0 |
0 |
|
|
X3 |
0 |
+1 |
-1 |
0 |
+1 |
-1 |
0 |
0 |
|
|
X4 |
0 |
0 |
+1 |
-1 |
0 |
0 |
0 |
0 |
|
|
X5 |
0 |
0 |
0 |
0 |
0 |
+1 |
+1 |
0 |
Свойства:
- сумма элементов каждого столбца матрицы равна 0;
- любой определитель, содержащийся в матрице, дожжен быть равен 0, +1, -1;
- любой определитель матрицы инцидентности, соответствующий замкнутому контуру, всегда равен 0.
ОПТИМИЗАЦИЯ ГРАФОВ.
Оптимизация неориентированных графов производится только в взвешенных графах. В этом случае оптимизация заключается в составлении минимально покрывающего дерева.
Минимально покрывающее дерево – это дерево, вес которого минимален
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.