Спутниковые измерения. Математическая обработка результатов геодезических измерений. Съемка местности, страница 4

h = dtgν

Дифференцируя по переменным d и υ и используя формулу общего вида (10.5) получим

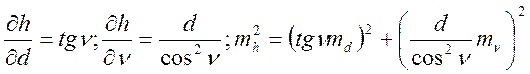
Подставляя в эту формулу исходные данные, получаем

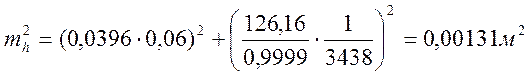
где 3438´ ­ число минут в радиане. Окончательно m_h = 0,036 м.

Для многих частных случаев, когда искомая величина находится путем выполнения простых арифметических действий формула (10.5) упрощается. Рассмотрим простую линейную функцию

u = k₁ x + k₂ y…,

где k ­ численные коэффициенты, а x и y ­ независимые перменные.

Согласно формуле (10.5)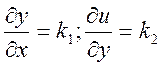

M_u²  = k₁²m_x²  + k₂²m_y².....

Если коэффициенты k₁ и k₂ равны единице, то получаем формулу m_u² = m_x² + m_y² , которая справедлива и для функции u = x - y.

Пример. При геометрическом нивелировании превышение вычисляется как разность отчетам по рейкам, h=a-b. Отчеты берутся с точностью 2 мм. Средняя квадратическая погрешность превышения

Если дана функция u = x₁ ± x₂ ± … ± x_n, то согласно (10.5) квадрат средней квадратической погрешности этой функции равен

m_u² = m₁² ± m₂² ± … ± m_n²

при m₁=m₂=…=m будем иметь m_u=m

Пример. Линия длиной 500 м измерена 20 м лентой. Средняя квадратическая погрешность одной ленты равна 0,01 м.

m_d = 0,01= 0,05 м.

10.5 Математическая обработка результатов равноточных измерений

При многократных равноточных измерениях одной и той же величины за окончательный результат измерений принимают среднее арифметическое из результатов отдельных измерений. Из свойства компенсации (10.2) следует, что с увеличением числа измерений сумма случайных погрешностей, деленная на их число, стремится к нулю и, следовательно, при бесконечно большом числе измерений сумма их результатов деленная на их число, т. е. среднее арифметическое значение, называемое арифметической срединой L будет равным истинному значению Х.

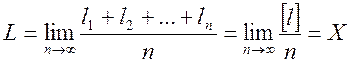                               (10.6)

При конкретном конечном числе измерений значение арифметической средины является вероятнейшем значением определяемой величины.

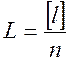                                                 (10.7)

Средняя квадратическая погрешность каждого отдельного измерения вычисляется по уклонениям от арифметической средины по формуле предложенной Бесселем.

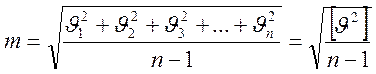                              (10.8)

где  есть уклонение результата измеряемой величины от арифметической средины.

Для определения средней квадратической погрешности арифметической средины M представим формулу (10.7) в следующем виде:

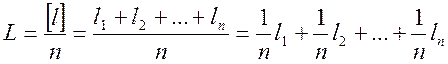
Так как величина погрешности каждого измерения оценивается соответствующей средней квадратической погрешностью m, то квадрат средней квадратической погрешности арифметической средины будет равен:

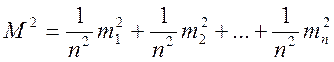
При равноточных измерениях m₁ = m₂=…= m. Тогда 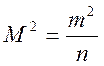  и

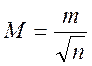                                                 (10.9)

Формула (10.9) служит не только для оценки точности определения арифметической средины из ряда равноточных измерений, но и дает возможность найти необходимое, минимальное количество измерений для достижения заданной точности.

Пример. Средняя квадратическая погрешность измерения равна m = 1см. Сколько раз необходимо повторить измерения, чтобы погрешность среднего из результатов была M = 0,5 см.

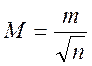   откуд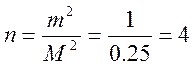а    раза

Математическая обработка ряда результатов многократных равноточных измерений некоторой геодезической величины выполняется в следующей последовательности:

1. Из результатов многократных измерений l вычисляют среднее арифметическое L

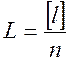
2. Вычисляют уклонения v каждого измерения от арифметической средины

Контроль: сумма всех уклонений должна быть равна нулю

3. Вычисляют квадрат каждого уклонения v×v и затем находят их сумму [v+ v]

4. По формуле Бесселя определяют среднюю квадратическую погрешность одного измерения

.

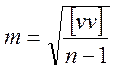5. Вычисляют среднюю квадратическую погрешность среднего арифметического

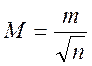
6. Определяют предельную погрешность результата измерения по формуле

∆_пр=3 m

При линейных измерениях определяют относительную погрешность по формуле

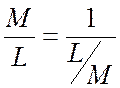
10.6 Обработка результатов неравноточных измерений

Неравноточными называют измерения, выполненные приборами различной точности, разным числом приемов, в различных условиях. Точность каждого из результатов измерений при неравноточных измерениях характеризуют своей среднеквадратической погрешностью. При обработке неравноточных измерений наряду со среднеквадратической погрешностью пользуются весом, вычисляемым по формуле 

P = c / m²

где   с - произвольно выбранная постоянная.

Так, для ряда результатов измерений l₁, l₂, ..., l_n, полученных со средними квадратическими погрешностями  m₁ ,  m₂ , ..., m_n имеем веса

p₁ = c / m₁² ,  p₂ = c / m₂² , ..., p_n = c / m_n²                     (10.10)

Окончательное значение измеряемой величины находят как общую арифметическую середину (иначе - "весовое среднее") по формуле

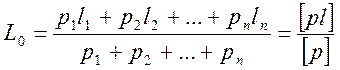                        (10.11)

  Среднюю квадратическую погрешность одного измерения, имеющего вес, равный единице, определяют по формуле

 ,

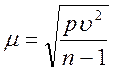где поправки   вычисляются по формулам

    

Правильность вычислений контролируют по формуле

Среднюю квадратическую погрешность общей арифметической середины L₀  находят по формуле

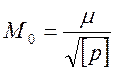
В том случае, когда с целью исследования того или иного прибора или метода измерялась величина, истинное значение которой Х  известно, то средняя квадратическая погрешность, измерения с весом единица, определяется формулой, аналогичной формуле Гаусса:

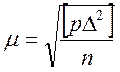
11. СЪЕМКА МЕСТНОСТИ

11.1. Общие сведения

Съемкой называется комплекс работ по созданию плана местности.

При применении цифровых технологий наряду с планом составляется цифровая модель местности.

          Съемки различают наземные, - когда работы по сбору информации о местности выполняются на земной поверхности, и аэрокосмические, - когда сбор информации о местности выполняется с помощью приборов, находящихся на летательных аппаратах (самолетах, искусственных спутниках Земли).

Наземные съемки в зависимости от применяемых приборов различают: теодолитную, мензульную, тахеометрическую, фототеодолитную.