Грубые погрешности, вызываемые небрежностью наблюдателя или неисправностью прибора, резко отклоняют результат измерения от истинного значения измеряемой величины. Такие погрешности выявляют путем повторных измерений и отбрасывают, бракуют.
Систематические погрешности входят в результаты измерений вследствие невыполнения поверок инструментов, компарирования мерных приборов, неучета атмосферных факторов и т.п. При повторных измерениях они остаются или постоянными, или изменяются по определенному закону. Такие погрешности должны быть обнаружены, изучены и исключены из результатов измерений путем введения соответствующих поправок, применением правильных методик измерений, своевременной юстировкой приборов.
Случайные погрешности при повторных измерениях меняются случайным образом, они неизбежны, и исключить их из результатов измерений невозможно. Поэтому, в ходе выполнения и обработки измерений стремятся лишь ослабить их влияние. Пути к такому ослаблению указывает теория погрешностей измерений. В дальнейшем будем полагать, что результаты измерений свободны от грубых и систематических погрешностей и содержат только случайные погрешности.
10.2 Свойства случайных погрешностей
Случайной погрешностью Δ называют отклонение результата измерения l от истинного значения измеряемой величины Х.
Δ = l – Х (10.1)
Теоретические исследования и многолетний опыт измерений показывает, что случайные погрешности подчинены определенным закономерностям, изучение которых дает возможность получить наиболее надежный результат и оценить его точность. Основные свойства случайных погрешностей следующие:
- при определенных условиях измерений, случайные погрешности по абсолютной величине не могут превышать известного предела;
- малые по абсолютной величине погрешности в данном ряду измерений появляются чаще, чем большие.
- одинаковые по абсолютной величине положительные и отрицательные погрешности равновозможны;
- среднее арифметическое из всех случайных погрешностей данного ряда равноточных измерений одной и той же величины при неограниченном числе измерений n стремится к нулю, т.е.
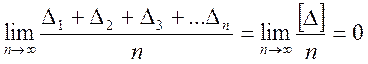 , где [ ] – знак
суммы (10.2)
, где [ ] – знак
суммы (10.2)
Формула (10.2) выражает свойство компенсации случайных погрешностей. Это свойство сохраняет и сумма попарных произведений случайных погрешностей, т. е.
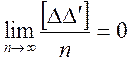 (n =
1, 2, 3 ... ∞) (10.3)
(n =
1, 2, 3 ... ∞) (10.3)
В результате многократных равноточных измерений получаемые значения измеряемой величины могут быть как больше, так и меньше ее истинного значения.
При установке критерия оценки точности измерений ставится условие его независимости от знаков отдельных погрешностей с учетом заметного отображения наибольшего из них. Таким требованиям удовлетворяет средняя квадратическая погрешность, предложенная Гауссом.
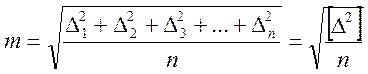 (10.4)
(10.4)
где Δ1, Δ2, …, Δn – случайные погрешности измерений.
Формула (10.4) дает точное значение средней квадратической погрешности при бесконечно большом числе n измерений. Оно носит название стандарт. При малом числе измерений вследствие случайного характера погрешностей Δi вычисленное по формуле (10.4) значение m имеет свои погрешности. Приближенно среднюю квадратическую погрешность определения по формуле (10.4) можно оценить по формуле
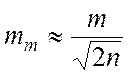
Формулой (10.4) пользуются при исследовании точности геодезических приборов и методов измерений, когда известно истинное значение измеряемой величины.
Доказано, что при нормальном распределении и достаточно большом числе измерений 68,3% всех случайных погрешностей по своему модулю не превышает средней квадратической погрешности m. Погрешности, превышающие 2m, встречаются редко, а больше 3m еще реже: 95,5% погрешностей по модулю меньше 2m и 99,7% погрешностей меньше 3m.
Утроенную среднюю квадратическую погрешность называют предельной погрешностью:
Δпред.=3m
На практике во многих работах за предельную погрешность принимают 2m. Измерения, содержащие ошибки больше предельной погрешности бракуют.
Средняя квадратическая погрешность дает характеристику точности по абсолютной величине, выражается в единицах измеряемой величины и называется абсолютной погрешностью.
В практике геодезических измерений в качестве
специальной характеристики точности используют относительные погрешности
отношение абсолютной погрешности к измеряемой величине ![]() ,
где l значение измеряемой величины.
,
где l значение измеряемой величины.
Характеристики относительной точности выражаются в процентах или в относительных величинах. Их используют в случае, когда точность результата измерения зависит от величины объекта измерения. К таким измерениям относятся линейные измерения.
10.4 Средняя квадратическая
погрешность функции измеренных величин
В практике геодезических измерений обычно определяемая величина является функцией других непосредственно измеряемых величин. Рассмотрим функцию многих независимых переменных общего вида
u = f(x,y,z…)
Дифференцируя это выражение и принимая дифференциалы за погрешности, предположив, что выполнено бесконечно много измерений, воспользовавшись формулами (10.2) и (10.4), В теории погрешностей измерений доказывается, что если x, y, z… независимые величины, а средние квадратические погрешности измеренных величин равны mx, my, mz, , то средняя квадратическая погрешность определяемой величины выражается формулой
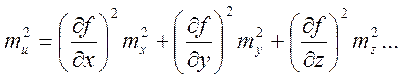 (10.5)
(10.5)
где
![]()
![]()
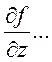 - частные производные
функции.
- частные производные
функции.
Таким образом, квадрат средней квадратической погрешности функции равен сумме квадратов произведений частных производных по каждой переменной, умноженных на квадраты их средних квадратических погрешностей.
Пример. Определить среднюю квадратическую погрешность измерения превышения методом тригонометрического нивелирования по измеренному расстоянию d = 124,16м и углу наклона υ = - 2°16´, если md = 0,06 м, а mυ = 1´.
Формула определения превышения при наведении на высоту инструмента имеет вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.