Санкт-Петербургский государственный политехнический университет
Кафедра автоматики и вычислительной техники
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ
Дисциплина: ТАУ. Тема:
Вынужденные колебания релейных систем.
Выполнил студент гр. 4081/1
Руководитель
Санкт-Петербург
2006
1. Цель работы
Цель работы – экспериментальное исследование синхронизации автоколебательных релейных систем внешним гармоническим воздействием
2. Программа работы
1) При подготовке к работе рассчитать параметры автоколебаний на входе нелинейного элемента типа идеального двухпозиционного реле в заданной системе.
2) Вычислить и построить зависимость порогового значения амплитуды синхронизации и фазы вынужденных колебаний соответственно от частоты и амплитуды гармонического воздействия.
3) Снять АФЧХ разомкнутой системы и экспериментальные зависимости, указанные в п.2.
3. Исследуемые схемы и исходные данные

Рис. 3.1. Исследуемая система
Передаточная функция линейной части системы: ![]()
Нелинейный элемент – идеальное двухпозиционное реле.
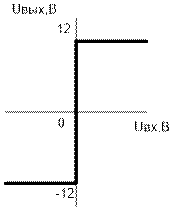
Рис.3.2. передаточная характеристика нелинейного элемента
4. Выполнение работы
При помощи программы Harmlin рассчитаем параметры автоколебаний. Для этого зададим передаточную функцию системы как комбинацию простейших звеньев и укажем их постоянные времени (для знаменателя): 0,00002 и дважды 0,0001, а также коэффициент усиления и вид нелинейности. В результате получим следующие параметры автоколебаний: A=0,53052 В
w=33166 1/с => f=5281 Гц
При выполнении работы получаем частоту автоколебаний порядка 3000 Гц.
Таблица 4.1. Экспериментальная АФЧХ системы
|
|
|
|
|
|
|
|
20 |
0 |
0 |
11,5 |
5,4 |
0,47 |
|
100 |
-0,01 |
0,06 |
11,5 |
5,4 |
0,47 |
|
200 |
-0,067 |
0,42 |
0,8 |
0,34 |
0,43 |
|
500 |
-0,15 |
0,94 |
0,5 |
0,21 |
0,42 |
|
1000 |
-0,23 |
1,44 |
0,5 |
0,105 |
0,21 |
|
3000 |
-0,46 |
2,90 |
0,25 |
0,02 |
0,057 |
|
6000 |
-0,625 |
3,93 |
0,34 |
0,005 |
0,015 |
|
12000 |
-0,56 |
3,53 |
0,33 |
0,001 |
0,003 |
Таблица 4.2. Экспериментальная
зависимость ![]()
|
|
|
|
150 |
0,01 |
|
200 |
0,0155 |
|
500 |
0,062 |
|
750 |
0,2 |
|
1000 |
0,36 |
|
1500 |
0,15 |
|
2000 |
0,068 |
Таблица 4.3.
Экспериментальная зависимость ![]()
|
|
|
|
0,5 |
1,54 |
|
0,7 |
1,35 |
|
1 |
1,082 |
|
0,5 |
0,88 |
|
2 |
0,68 |
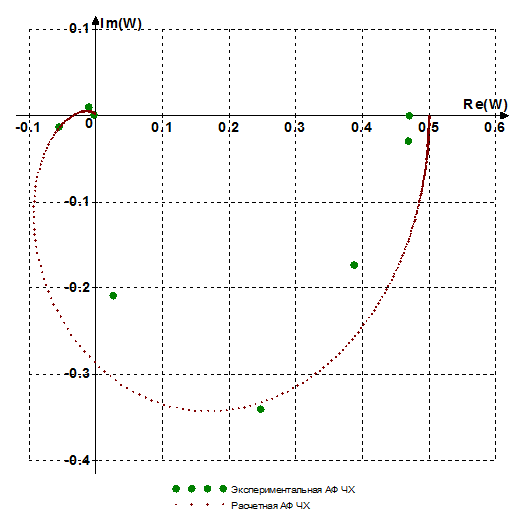
Рис.4.1. АФЧХ разомкнутой системы
Из геометрического решения уравнения вынужденных колебаний следует, что пороговое значение амплитуды внешнего воздействия соответствует модулю мнимой составляющей передаточной функции линейной части системы при данной частоте. А фаза вынужденных колебаний суть угол между вещественной осью и вектором разности годографа Найквиста и обратного коэффициента гармонической линеаризации (длина которого равна амплитуде входных колебаний при данной частоте.
Построим требуемые зависимости с помощью пакета MATLAB 6.5
logw=-2:0.01:4.5;
w=10.^logw;
W=0.5./((1e-4*j*w+1).*(1e-4*j*w+1).*(2e-5*j*w+1));
plot(w/(2*pi),abs(imag(W)));
Wk=0.5/((1e-4*j*33166+1)*(1e-4*j*33166+1)*(2e-5*j*33166+1));
Avh=0.1:0.01:5;
fi=asin(abs(imag(Wk))./Avh);
plot(Avh,fi);
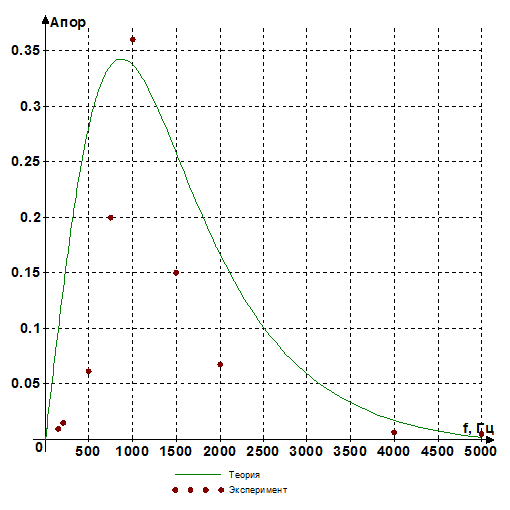
Рис.4.2. Зависимость Апор(w)
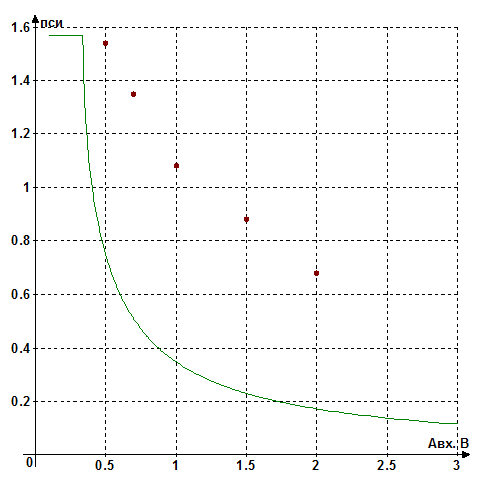
Рис.4.3.
Экспериментальная зависимость ![]() при f=1000Гц
при f=1000Гц
5. Выводы
Полученные результаты позволяют говорить: а) о наличии в системе вынужденных колебаний б) о том, что характер зависимости амплитуды колебаний от частоты возбуждения имеет нелинейный характер: в области низких и высоких частот амплитуда стремится к нулю, а максимум наблюдается при частоте порядка 1кГц в) зависимость фазы вынужденных колебаний также нелинейна, причем с увеличением амплитуды внешнего гармонического воздействия разность автоколебаний и внешнего сигнала уменьшается.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.