
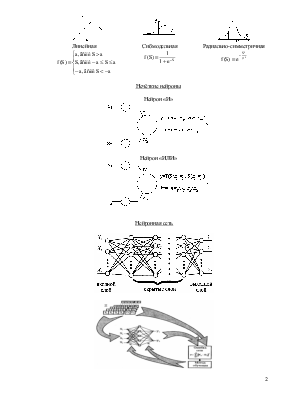




История развития ИНС.
1943-1956 – Маккалон и Питс – пороговый логический нейрон.
|
|
|
|
Пороговый логический нейрон Маккалона и Питтса (1956 г.) |
Многофункциональный логический триггер Леонтьева (1965 г.) |
1958 Ф. Розенблат – перцептрон (для распознавания образов)
1960 Б. Уидроу – адаптивный линейный элемент – «адалина»
1969 Минсайн и Пайперт - простая линейная сеть «madaline» (many adaline)
1982 Хопфилд – динамическая структура «сеть Хопфилда»
1988 группа РЭР – алгоритм обучения МНС – «метод обратного распространения ошибки» - «error back propagation method» (BP)
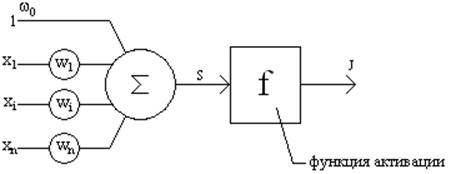
Структура искусственного нейрона.
![]()
![]()
![]()
|
|
|
|
|
Линейная
|
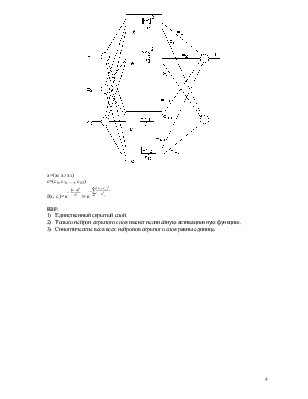
Сибмодельная
|
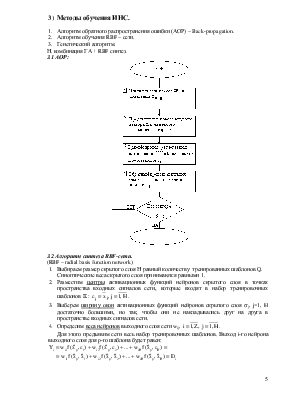
Радиально-симметричная
|
Нейрон «И»
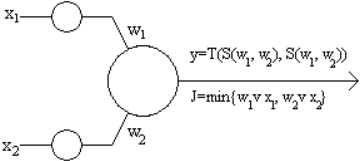
Нейрон «ИЛИ»
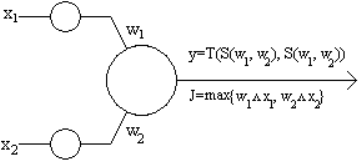
2) Применение ИНС
Проблемы, решаемые ИНС.
Классификация образов:
Задача состоит в указании принадлежности входного образа, представленого вектором признаков, одному или нескольким предварительно определённым классам. К известным приложениям относятся распознавание букв, распознавание речи, классификация сигнала электрокардиограммы, классификация клеток крови.
Кластеризация/категоризация:
При решении задачи кластеризации, которая известна также как классификация образов без учителя, отсутствует обучающая выборка с метками классов. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кластер. Известны случаи применения кластеризации для извлечения знаний, сжатия данных и исследования свойств данных.
Аппроксимация функций:
Предположим, что имеется обучающая выборка ((х1, у1)…((хN, уN)), которая генерируется неизвестной функцией, искаженной шумом. Задача аппроксимации состоит в нахождении оценки этой функции.
Предсказание/прогноз:
Пусть заданы N дискретных отсчётов {y(t1), …, y(tN)} в последова-тельные моменты времени t1, …, tN. Задача состоит в предсказании значения y(tN+1) в момент tN+1. Прогноз имеет значительное влияние на принятие решений в бизнесе, науке и технике.
Оптимизация:
Задачей оптимизации является нахождение решения, которое удовлетворяет системе ограничений и максимизирует (минимизирует) целевую функцию.
Память, адресуемая по содержанию:
Память, адресуемая по содержанию, или ассоциативная память, доступна по указанию заданного содержания (иногда даже искажённого), что, в свою очередь, обеспечивает более высокую надёжность при работе с ней.
Управление:
Расчёт такого входного воздействия u(t), при котором система следует по желаемой траектории, диктуемой эталонной моделью.
Классификация НС.
Три базовых типа:
1. Самоорганизующиеся сети Кохонеса.
С обучением без «учителя».
2. Динамические сети Хопфилда.
С обучением по методу последовательного подкрепления знаний
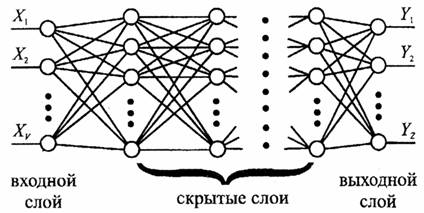
3. Сети прямого распределения (перцептронные сети)
С обучением с «учителем».
Это решения задач управления, которые в основном применяются в статических МНС прямого распространения с обучением по методу ВР.
Классическая RBF-сеть – сети с простой настройкой и не требует рекурсии.
RBF – radial basis function networks.
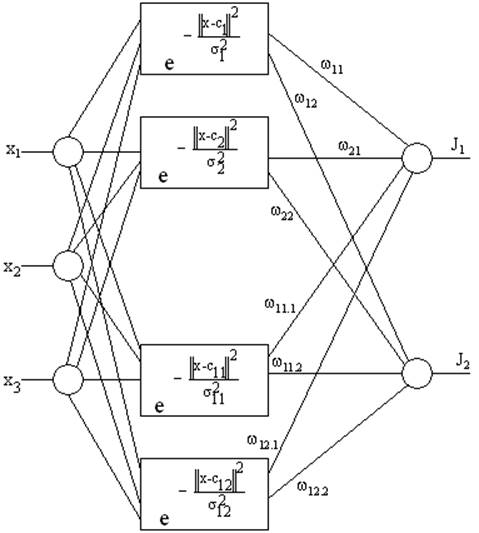
x=(x1 x2 x3)
c=(c1, c2, …, c12)
f(x, c)=![]()
RBF:
1) Единственный скрытый слой.
2) Только нейрон скрытого слоя имеют нелинейную активационную функцию.
3) Синоптические веса всех нейронов скрытого слоя равны единице.
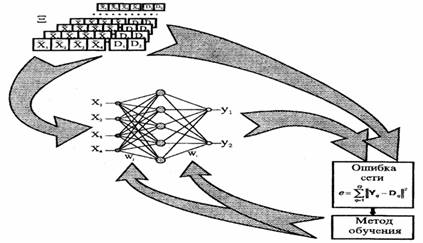
3) Методы обучения ИНС.
1. Алгоритм обратного распространения ошибки (АОР) – Back-propagation.
2. Алгоритм обучения RBF – сети.
3. Генетический алгоритм.
Н. комбинация ГА + RBF синтез
3.1 АОР:
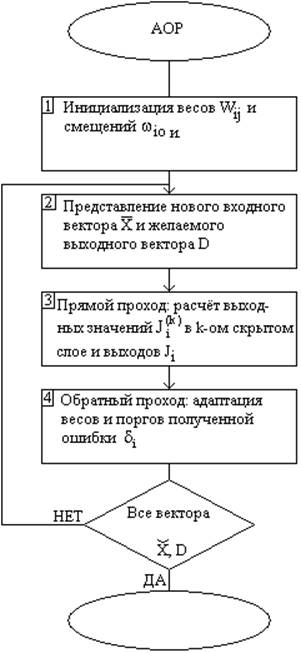
3.2 Алгоритм синтеза RBF-сети.
(RBF – radial basis function network)
1. Выбираем размер скрытого слоя Н равный количеству тренированных шаблонов Q.
Синоптические веса скрытого слоя принимаются равными 1.
2.
Разместим центры активационных функций нейронов скрытого слоя в
точках пространства входных сигналов сети, которые входят в набор тренировочных
шаблонов ![]() :
:
![]() .
.
3. Выберем ширину окон активационных функций нейронов скрытого слоя sj, j=1, H достаточно большими, но так, чтобы они не накладывались друг на друга в пространстве входных сигналов сети.
4.
Определим веса нейронов выходного слоя сети wij,
![]() .
.
Для этого предъявим сети весь набор тренировочных шаблонов. Выход i-го нейрона выходного слоя для p-го шаблона будет равен:
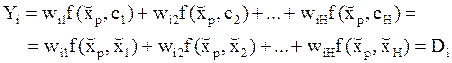
Расписав эти уравнения для всех выходов сети и всех шаблонов, получим следующее уравнение в матричной форме:
ÆwT=D, где
Æ=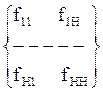 -
интерполяционная матрица,
-
интерполяционная матрица, ![]() ;
;
W=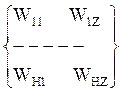 -
матрица выходных синоптических весов;
-
матрица выходных синоптических весов;
D=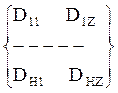 -
матрица выходных шаблонов.
-
матрица выходных шаблонов.
![]()
Решение: WT=Æ-1D
Основная сложность – это формирование тренировочных шаблонов.
3.3 ГА – генетические алгоритмы.
ГА – является процедурой глобальной оптимизации и зиждется на гипотезе селекции: чем выше приспособленность особи, тем выше вероятность того, что в её потомстве признаки определяющие приспособленность будут выражены ещё сильнее.
3.3.1 Представление генетической информации.
Подобно тому, как природный хромосомный материал представляет собой линейную последовательность различных комбинаций четырёх нуклеотидов (А – аденин, Ц – цитозин, Т – тимин, Г – гуанин), вектора переменных в ГА зашифровываются в виде цепочек символов, закодированных в коде Грея.
|
X |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
|
A |
1101 |
1100 |
0101 |
1000 |
0101 |
1001 |
Генетические операторы:
Кроссовер – Мутация – Инверсия
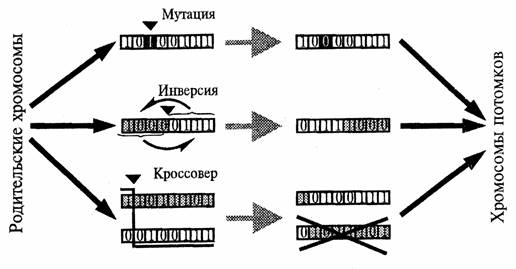
Репродуктивный план Холланда:
Шаг 1. Инициализация начальной популяции
Шаг 2. Выбор родителей для скрещивания
Шаг 3. Формирование генотипа потомка
Шаг 4. Отбор особи на этипинирование и замена её потомком.
Шаг 5. Определение приспособленности потомка
Одна из нейросходящихся версий ГА:
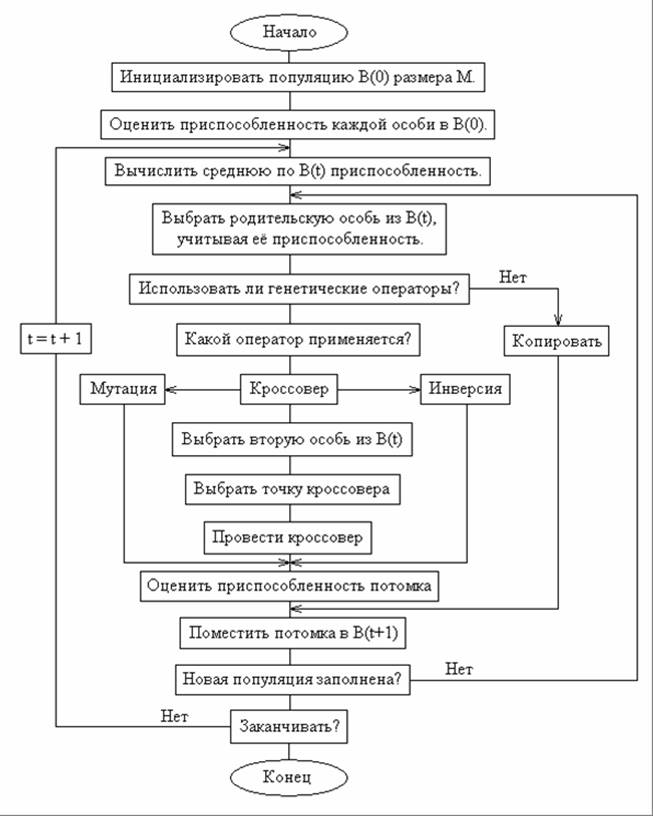
3.4 Комбинированная настройка.
RBF – сети с ГА.
ГА – выбирает в таких точках пространства входных сигналов сети
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.