













Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Компьютерных Систем и Программных Технологий
ОТЧЕТ
по лабораторной работе №12-13
«Исследование оптимальной системы ЛК-управления с наблюдателями Люенбергера и Калмана»
по предмету «Компьютерные системы управления»
Работу выполнили студент группы 5081/1
студентка группы 5081/10
Преподаватель ____________
Санкт-Петербург
2011
1. Цель работы
1.1. Исследование системы с наблюдателем Люенбергера
Изучение структуры построения и особенностей работы оптимальной системы ЛК-управления с наблюдателем Люенбергера. Оценка эффективности применения наблюдателя в оптимальной системе ЛК-управления по начальным условиям.
1.2. Исследование системы с наблюдателем Калмана
Изучение организации, методов синтеза и исследование особенностей работы оптимальной системы ЛК-управления с наблюдателем Калмана.
2. Методика исследования
2.1. Система с наблюдателем Люенбергера
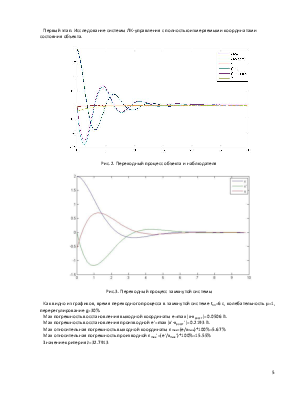
Как известно, оптимальное управление линейным объектом с использованием квадратичного критерия оптимальности (ЛК-управление) осуществляется в форме пропорционального управления по всем координатам состояния объекта.
Если часть координат не может быть измерена, то при синтезе оптимального ЛК-управления применяются специальные восстановители (наблюдатели) неизменяемых координат состояния в форме специальных корректирующих динамических моделей.
Так как наблюдатель Люенбергера является модифицируемой динамической моделью исходного объекта, используемой для формирования полного вектора координат состояния объекта, то главной системной проблемой будет оценка динамических процессов, происходящих в такой усложненной наблюдателем системе управления. В конечном итоге, эта проблема сводится к оценке эффективности применения наблюдателей в оптимальных системах ЛК-управления.
Для ее решения в работе используется экспериментальный метод сравнительного анализа работы систем ЛК-управления различной структуры. Из анализа структуры системы с наблюдателем можно предположить, что динамика таких систем будет существенно зависеть от возможных задержек формирования сигналов управления регулятором (сигналов обратной связи). Основными причинами появления запаздывания в рассматриваемой системе являются:
- запаздывание формирования корректирующего сигнала;
- включение в систему последовательно с объектом дополнительного динамического элемента (наблюдателя), размерность и параметры которого идентичны исходному объекту. Первый вид запаздывания относится к типу «чистого», или «транспортного» запаздывания. В частности, его источником является то, что в дискретных системах изменение координат состояния для (k+1)-го момента времени производится по измерениям, выполненным в k-й момент времени.
Другая причина появления этого вида запаздывания связана с тем, что в цифро-аналоговых системах (непрерывный объект и цифровой регулятор) возникают проблемы синхронизации запуска непрерывной и дискретной частей системы. Так как в данной работе используется цифро-аналоговый комплекс, то эта причина может быть определяющей.
Уравнение управляемого объекта:
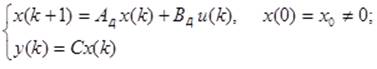
Уравнение наблюдателя:
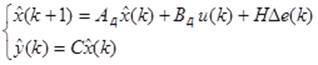
![]() - вектор коррекции координат состояния
- вектор коррекции координат состояния
Уравнение регулятора:
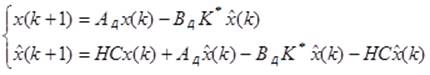
2.2. Система с наблюдателем Калмана
Как известно, организация систем оптимального терминального управления с интегральным квадратичным критерием качества (системы ЛК - управления) требует знания всех координат состояния объекта управления.
В случае, когда часть из этих координат по каким-либо причинам не измеряемы, реализация ЛК-управления возможна, если в системе производится их восстановление. Известны различные способы построения таких восстановителей, получивших в литературе название наблюдателей. Если объект и измеритель координат находятся под воздействием случайных помех, в качестве наблюдателя наибольшее распространение получил фильтр Калмана.
Наблюдатели для восстановления неизмеряемых координат, как правило, используют идею применения адекватной объекту математической модели, в которой доступны для измерения все координаты. Эти координаты и применяются при синтезе оптимального управления. С целью уменьшения влияния задержек, в наблюдателе Калмана реализуются прогнозируемые на такт вперед значения координат состояния объекта.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.