Исследование оптимальной системы ЛК-управления с наблюдателями Люенбергера и Калмана. Исследование системы с наблюдателем Люенбергера, страница 2

Так как прогнозируемые и реальные (измеряемые) их значения неизбежно отличаются, в структуру фильтра Калмана включена цепь коррекции прогнозируемого значения координат. Для этой коррекции и используется  рассогласование (невязка) между реальными (измеряемыми) и прогнозируемыми координатами  состояния.

Чтобы оценить эффективность применения наблюдателей, существенно усложняющих структуру управления по сравнению  с системой без наблюдателя, в данной работе используется метод экспериментальной оценки сравниваемых систем.  При этом следует  учитывать, что в системе с наблюдателем, помимо задачи восстановления неизмеряемых координат решается также задача фильтрации помех. В ряде случаев эта задача может быть даже определяющей.

Уравнение объекта:

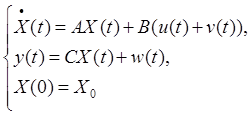
Уравнение наблюдателя:

3. Исходные данные

a₀=1

a₁=0.5

a₂=1

T₀=0.2 c

x(0)=x₀=2 В

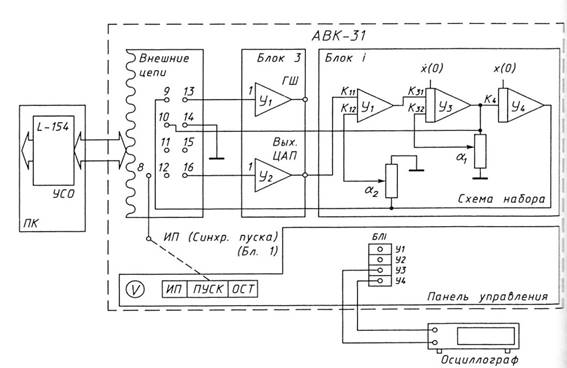
Рис.1. Схема набора

4. Экспериментальное исследование

4.1. Исследование системы с наблюдателем Люенбергера

Перед началом исследования системы были рассчитаны параметры дискретного объекта:

                   

Также были рассчитаны математическое ожидание и дисперсия шума:

M=0.125

D=0.399

Первый этап. Исследование системы ЛК-управления с полностью измеряемыми координатами состояния объекта.

Рис.2. Переходный процесс объекта и наблюдателя

Рис.3. Переходный процесс замкнутой системы

Как видно из графиков, время переходного процесса в замкнутой системе t_пп=6 c, колебательность µ=1, перерегулирование g=30%.

Max погрешность восстановления выходной координаты e=max|x-x_восст|=0.0506 В.

Max погрешность восстановления производной e’=max|x’-x_восст’|=0.2193 В.

Max относительная погрешность выходной координаты ε_max=(e/x_max)*100%=5.67%

Max относительная погрешность производной ε_max’=(e’/x_max’)*100%=15.55%

Значение критерия J=32.7913

Второй этап. Исследование системы ЛК-управления с не полностью измеряемыми координатами состояния объекта.

Оценка чистого запаздывания.

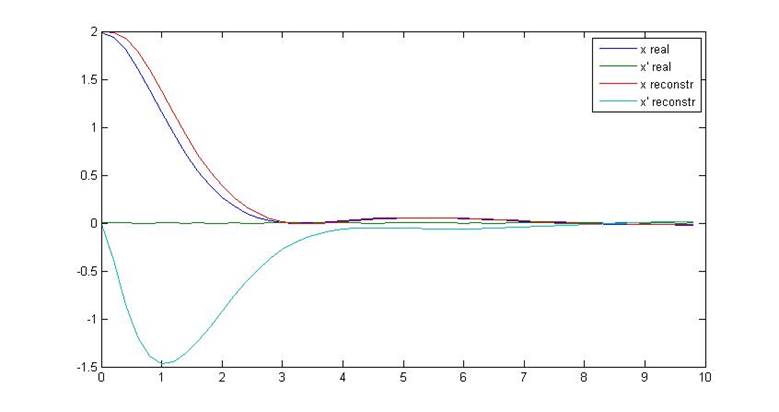
Рис.4. Переходный процесс объекта и наблюдателя

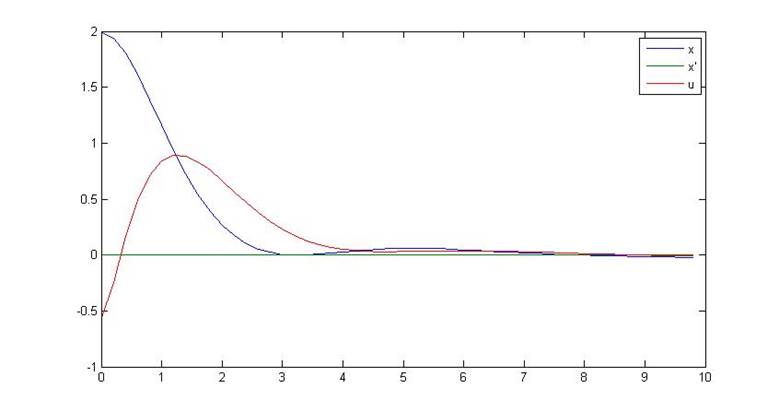
Рис.5. Переходный процесс замкнутой системы

Параметры переходного процесса в замкнутой системе:

t_пп=8 c

µ=1

g=5.5%

J=44.0669

Оценка влияния инерционного запаздывания.

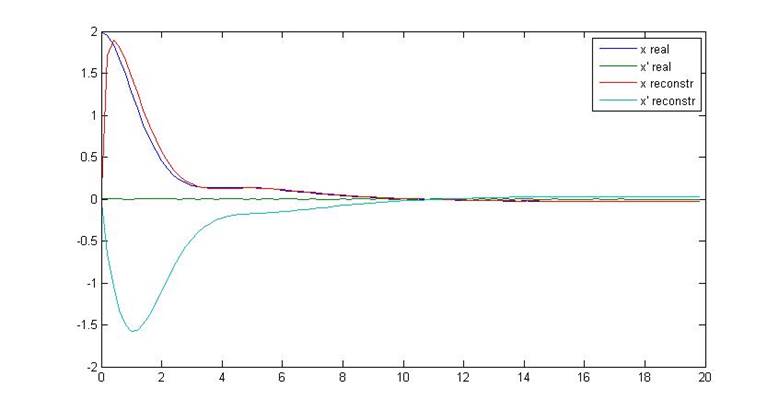
Рис.6. Переходные процессы объекта и наблюдателя

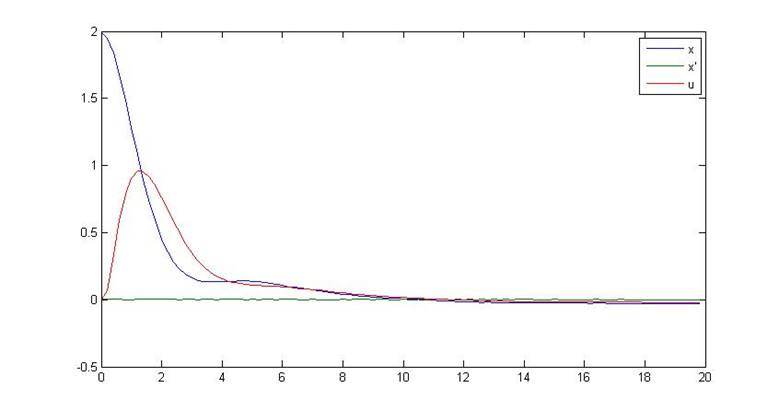
Рис.7. Переходный процесс замкнутой системы

Параметры переходного процесса в замкнутой системе:

t_пп=10 c

µ=1

g=14%

J= 48.2226

Третий этап. Исследование квазиоптимальной системы ЛК-управления.

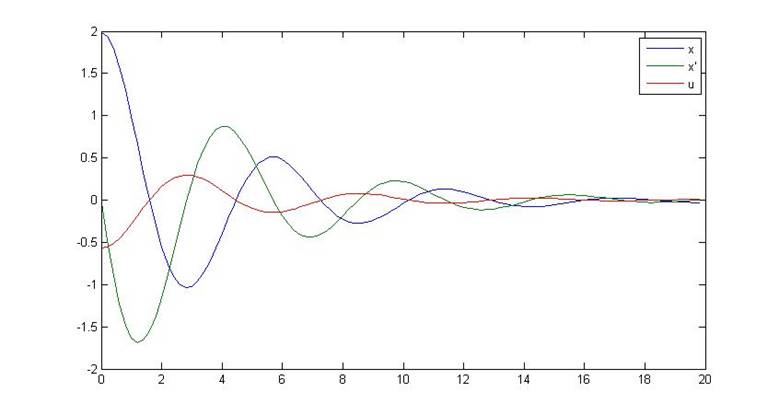
Рис.8. Переходный процесс в квазиоптимальной системе с полностью измеряемыми координатами, K₂=0

Параметры переходного процесса:

t_пп=18 c

µ=6

g=100%

J= 56.1545

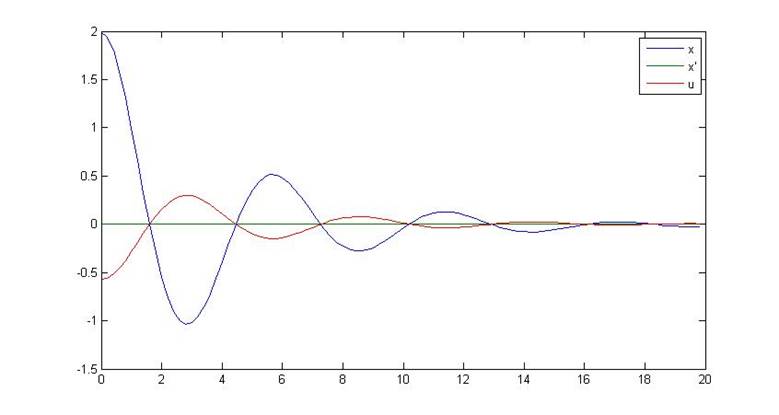
Рис.9. Переходный процесс в квазиоптимальной системе с не полностью измеряемыми координатами

Параметры переходного процесса:

t_пп=20 c

µ=7

g=104%

J= 29.1179

Четвертый этап. Исследование системы ЛК-управления при воздействии шумов.

Для данного исследования была выбрана система с полностью измеряемыми координатами, K₂=0.

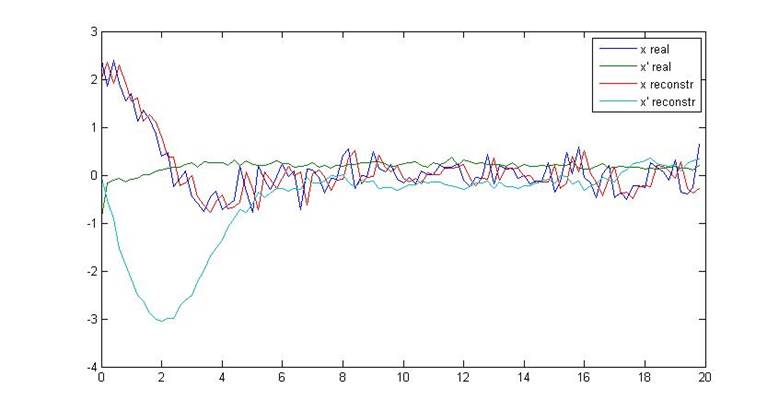
Рис.10. Переходные процессы объекта и наблюдателя

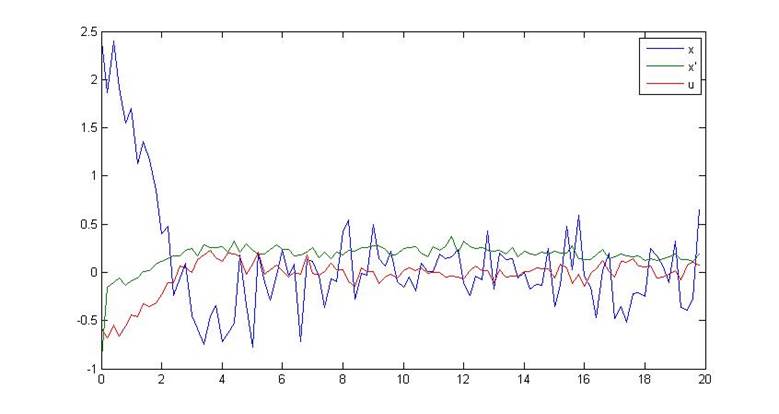
Рис.11. Переходный процесс замкнутой системы

Как видно из приведенных графиков, наблюдатель Люенбергера не справляется с задачей фильтрации помех и, следовательно, не может использоваться в системах, подвергающихся воздействию шумов.

Определить параметры переходного процесса в данном случае не представляется возможным.

Значение критерия J= 155.7041

4.2. Исследование системы с наблюдателем Калмана

Параметры дискретной модели, как и значения математического ожидания и дисперсии, аналогичны таковым из исследования системы с наблюдателем Люенбергера.

4.2.1. Исследование системы без воздействия шума.

Исследование системы при K₁=K₂=0

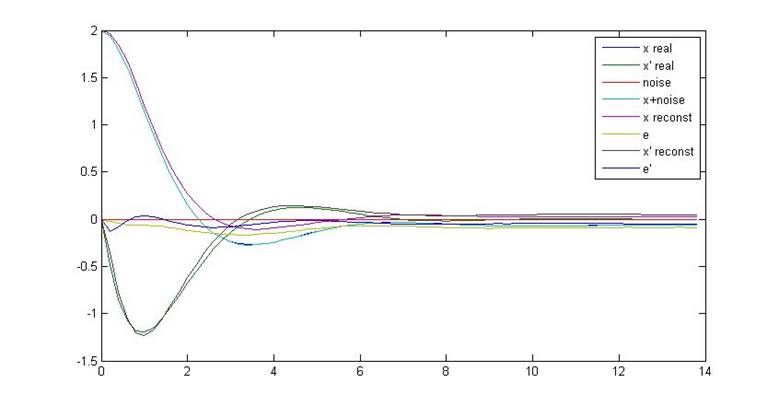
Рис.12. Переходные процессы объекта и наблюдателя

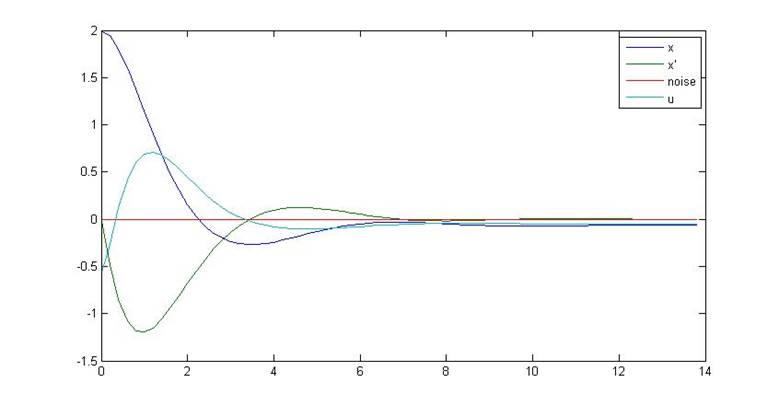
Рис.13. Переходный процесс замкнутой системы

Параметры переходного процесса замкнутой системы:

t_пп=7 c

µ=1

g=30%

J= 33.4207

Однако, как видно из приведенных графиков, в данном случае имеет место статическая ошибка, вносящая погрешность в значение x_f и делающая его отличным от нуля (более того – при подаче на вход системы нулевого сигнала в системе наблюдались переходные процессы). Для устранения статической ошибки в параметрах программы математическое ожидание было выставлено равным нулю, после чего повторено снятие данных при тех же параметрах системы.

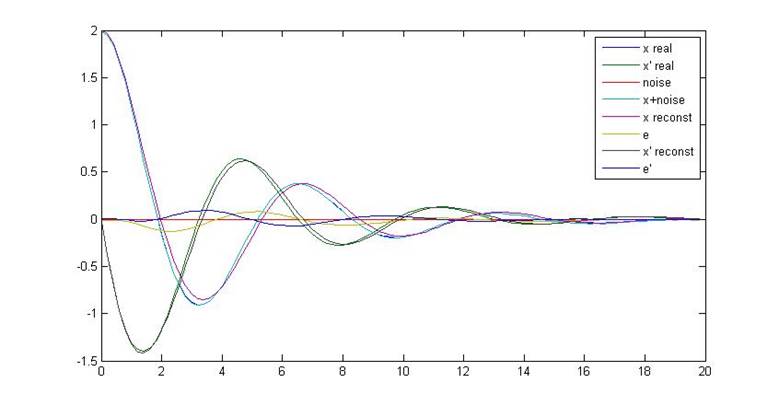
Рис.14. Переходные процессы объекта и наблюдателя

Рис.15. Переходный процесс в замкнутой системе