Оценка неизмеряемых координат состояния объекта при случайных возмущениях (дискретный фильтра Калмана)

1.  Цель работы

Ознакомление с организацией и особенностью работы дискретного фильтра Калманаа, предназначенного для оценки неизмеряемых координат состояний объекта, находящегося под воздействием помех типа белого шума как на входе, так и в канале измерения выходного сигнала.

2.  Исходные данные

В настоящей работе рассматривается объект, математическая модель которого - дифференциальное уравнение второго порядка.

a₀ = 1

a₁ = 1

a₂ = 2

b = 2

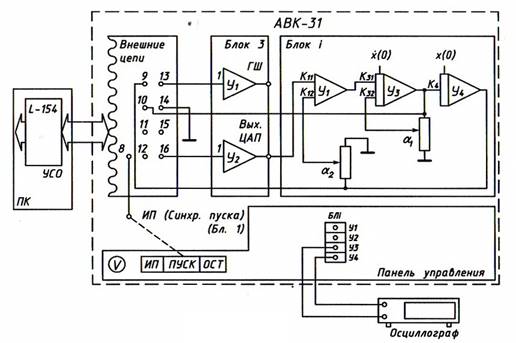
Рис. 4.1. Схема набора

Тогда дифференциальное уравнение системы имеет вид:

Параметры непрерывной модели

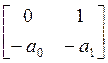Х =          А==              В==

3.  ВЫполнение работы

3.1  Исследование работы модели при различных периодах дискретизации

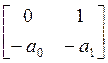Х =          А==              В==

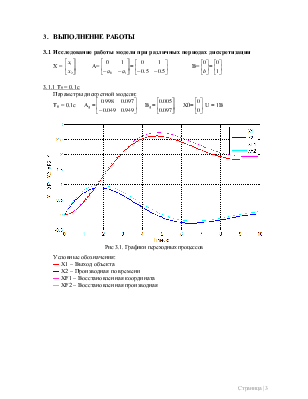
3.1.1 Т₀ = 0.1с

Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0= U = 1В

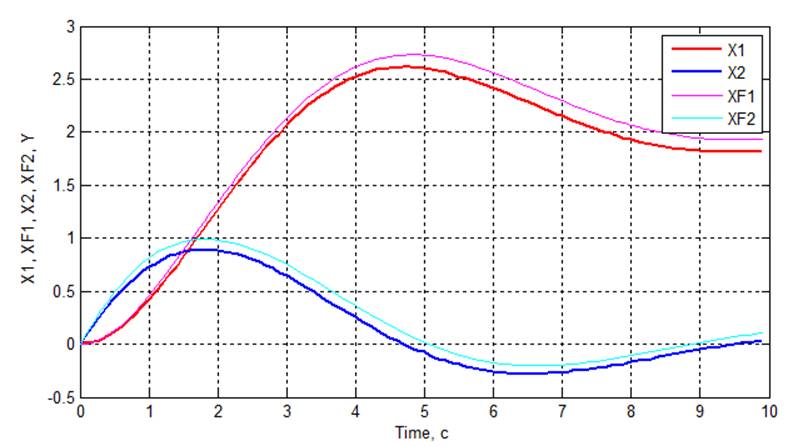
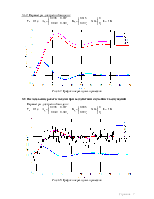
Рис 3.1. Графики переходных процессов

Условные обозначения:

▬ X1 – Выход объекта

▬ X2 – Производная по времени

▬ XF1 – Восстановленная координата

▬ XF2 – Восстановленная производная

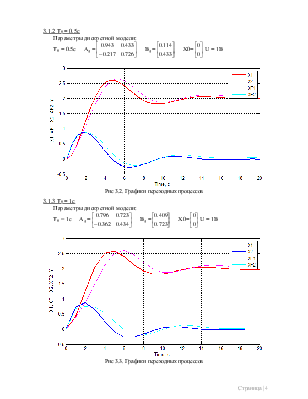
3.1.2 Т₀ = 0.5с

Параметры дискретной модели:

Т₀ = 0.5с     А_д =     В_д =     X0= U = 1В

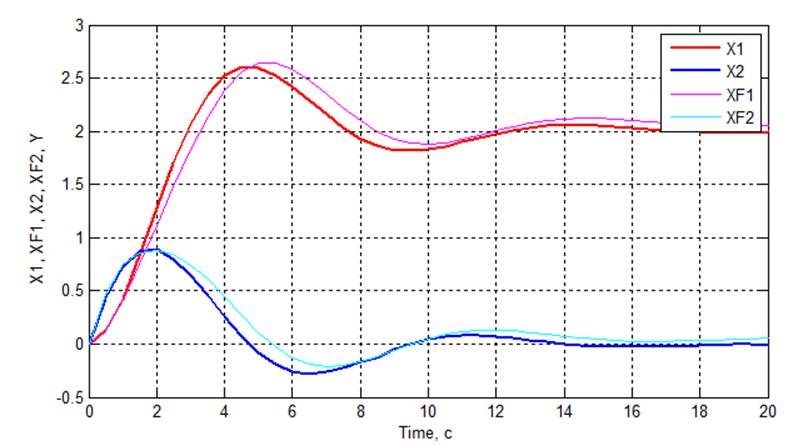
Рис 3.2. Графики переходных процессов

3.1.3 Т₀ = 1с

Параметры дискретной модели:

Т₀ = 1с     А_д =     В_д =     X0= U = 1В

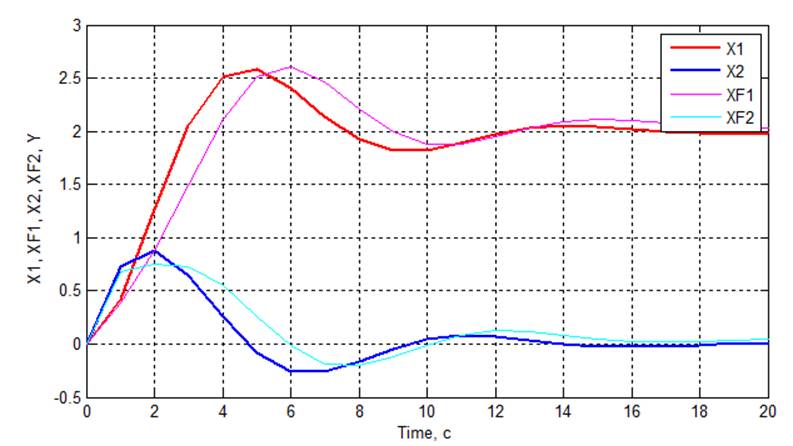
Рис 3.3. Графики переходных процессов

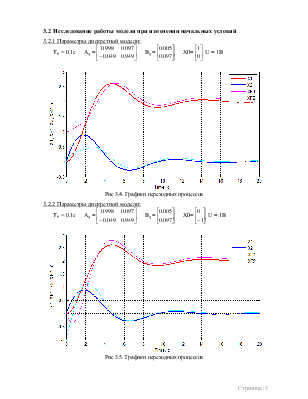
3.2  Исследование работы модели при изменении начальных условий

3.2.1 Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0= U = 1В

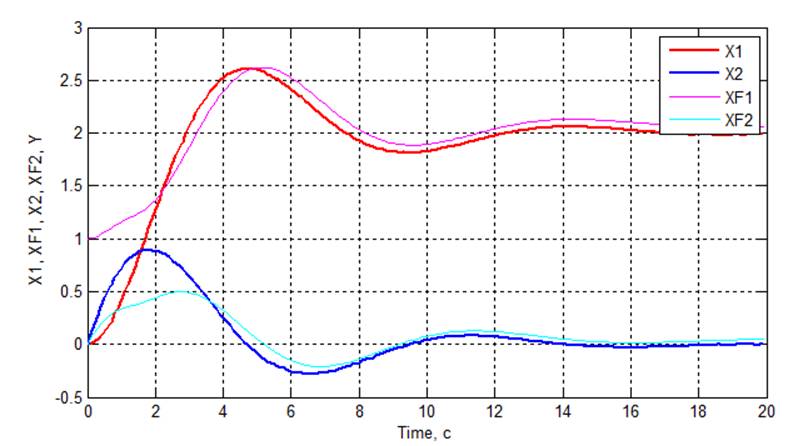
Рис 3.4. Графики переходных процессов

3.2.2 Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0= U = 1В

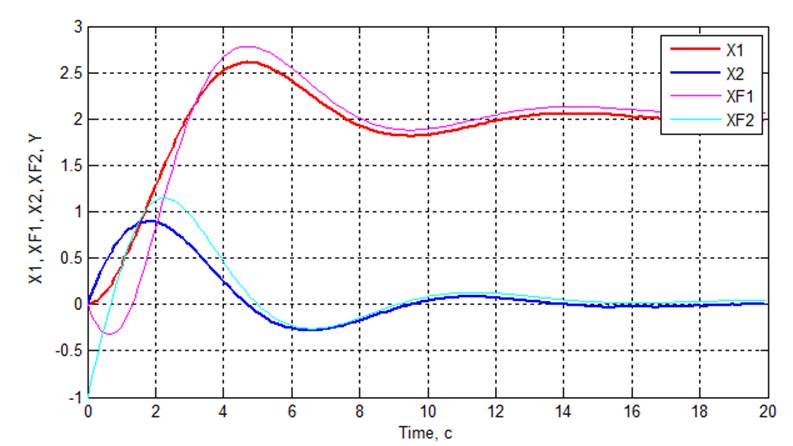
Рис 3.5. Графики переходных процессов

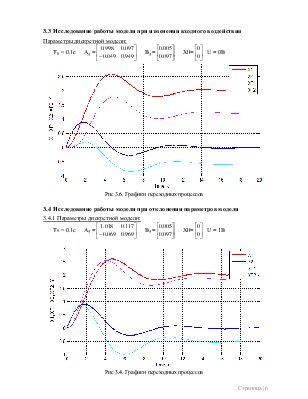
3.3  Исследование работы модели при изменении входного воздействия

Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0=  U = 0В

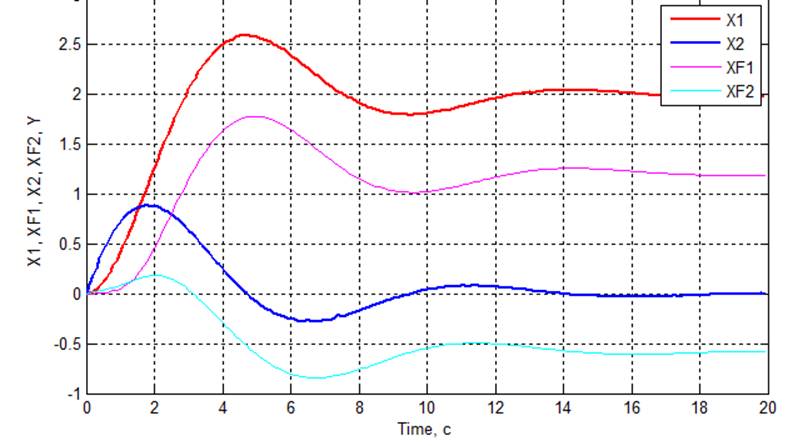
Рис 3.6. Графики переходных процессов

3.4  Исследование работы модели при отклонении параметров модели

3.4.1 Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0=  U = 1В

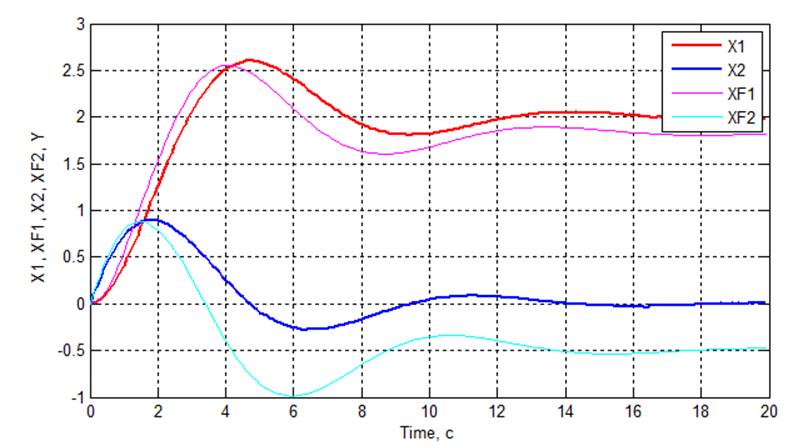
Рис 3.4. Графики переходных процессов

3.4.2 Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0= U = 1В

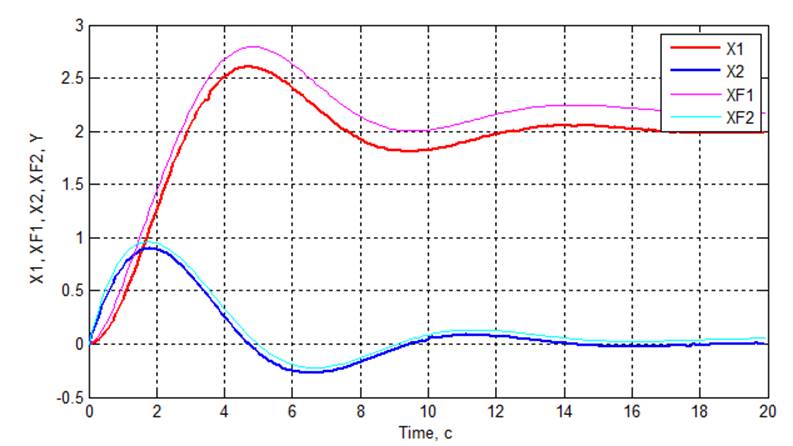
Рис 3.7. Графики переходных процессов

3.5  Исследование работы модели при воздействии случайных возмущений

Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0= U = 1В

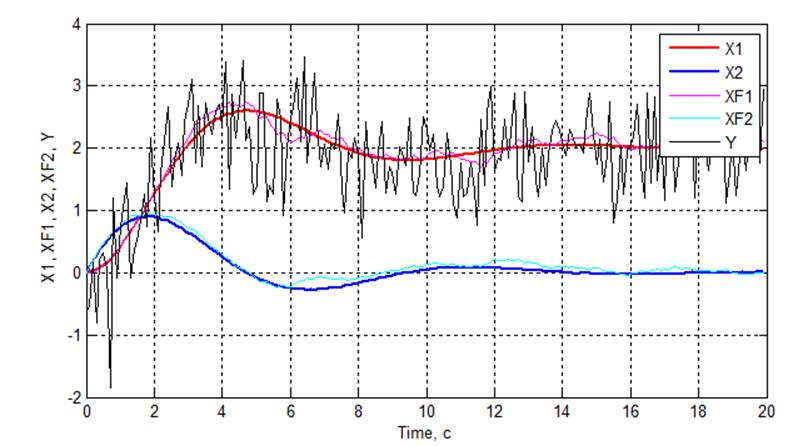
Рис 3.8. Графики переходных процессов

4.  ВЫводы

1.  Различные периоды дискретизации не влияют на поведение модели, координаты восстанавливаются с погрешностью не  более 10%.

2.  При изменении начальных условий модели подстройка до уровня 10% погрешности занимает порядка 4-5 с.

3.  Изменение значения возмущающего воздействия даёт существенное расхождение, что свидетельствует о некорректной работе модели. Из этого можно сделать вывод о том, что для наилучшего результата необходимо как можно точнее устанавливать данный параметр.

4.  Отклонение параметров модели от истинных так же приводит к некорректной работе модели

5.  Наличие шума незначительно влияет на адекватность работы модели, тк фильтр Калмана учитывает параметры шума при моделировании объекта.

Таким образом можно сделать вывод о том, что дискретность и начальные условия не влияют на адекватность работы фильтра, а параметры модели и значение возмущающего воздействия существенно сказываются на работе фильтра.