Спектры непериодических сигналов. Спектральное представление непериодических сигналов. Спектр прямоугольного видеоимпульса

Лекция 9-10

Спектры непериодических сигналов

1. Спектральное представление непериодических сигналов.

2. Спектр прямоугольного видеоимпульса.

3. Спектр прямоугольного радиоимпульса.

4. Спектр колоколообразного импульса.

5. Спектр экспоненциального импульса.

6. Преобразование Фурье и спектр дельта-функции и функции включения.

7. Спектр серии импульсов.

8. Распределение энергии в спектре. Энергетический спектр и его эффективная ширина.

1. Очень важными на практике являются непериодические импульсы: одиночные импульсы, серии импульсов. Они не могут быть представлены в виде ряда Фурье или же тригонометрического ряда.

Чтобы применить к ним спектральный метод описания, нужно считать эти сигналы периодическими функциями с периодическим стремлением к .

Тогда и представление непериодического сигнала по Фурье может рассматриваться при .

Воспользуемся более удобной комплексной формой ряда Фурье (лекция 4):

                                                                                        (1)

где комплексные амплитуды рассчитываются:

                                                                 (2)

Подставим (2) в (1), обозначив интервал между соседними частотами гармоник: , получим (3):

   

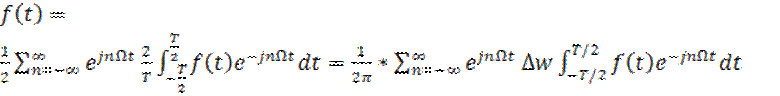
При увеличении T, амплитуда  уменьшается, интервал  уменьшается, линейный спектр згущается.

В пределе при , .

Спектр из дискретного становится сплошным, при этом сумма в правой части (3) переходит в интеграл:

                                                               (4)

(4) представляет сумму гармонических функций с бесконечно малыми функциями с частотами w, проходящими весь спектр от  до .

Непериодические сигналы характеризуются непрерывным спектром частот, в отличии от периодических – где спектр дискретный.

                                                                                      (5)

                                                                                 (6)

(5) – прямое преобразование Фурье (ППФ).

(6) – обратное преобразование Фурье (ОПФ).

 - ППФ.

 - ОПФ.

ППФ позволяет перейти из временной области на комплексную частотную плоскость, а ОПФ – наоборот.

Основные свойства преобразование Фурье:

1. Линейность:

 

2. Теорема дифференцирования:

 

3.  

4. Теорема подобия (масштаба):

 

5. Теорема о сдвиге:

 

6. Теорема о свертке:

 

 

7. Теорема Рэлея:

 

 - спектральная плотность сигнала.

Проводя аналогию между разложением Фурье и интегралом Фурье, запишем:

 

 

                                                                       (7)

 

Следовательно, спектральная плотность имеет физический смысл плотности амплитуд и обладает размерностью амппилитуды/Герц.

S(jw) – характеризует гармонику частоты w по амплитуде и фазе.

Из (7): огибающая АЧС S(w) непериодической функции и огибающая дискретного спектра Cn(w) функции периодически совпадает по форме и отличается лишь масштабом S(w)=π/Ώ Cn(w).

ППФ и ОПФ имеют симметрическую природу и это обусловлено дуальностью частоты и времени.

                                                                            (8)

                                                                     (9)

Другими словами, если спектром f(t) является функция S(w), то спектром S(t) будет функция 2πf(w).

2. Пусть дан сигнал U(t) – одиночный прямоугольный видеоимпульс.

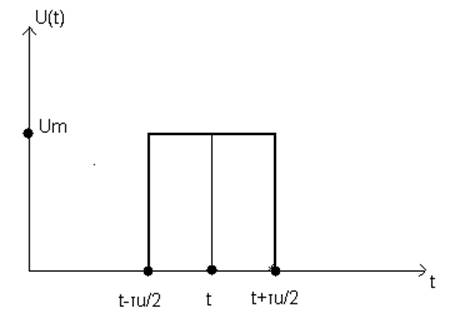
Рисунок 1

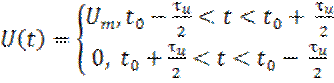                                                                     (10)

 - длительность импульса.

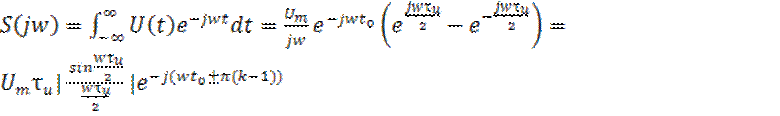                                                                              (11)

K=1,2,3,…,N.

                                                                                         (12)

                                              (13)

АЧС существенно зависит от , но не связано с . ФЧС наоборот определено временем запаздывания .

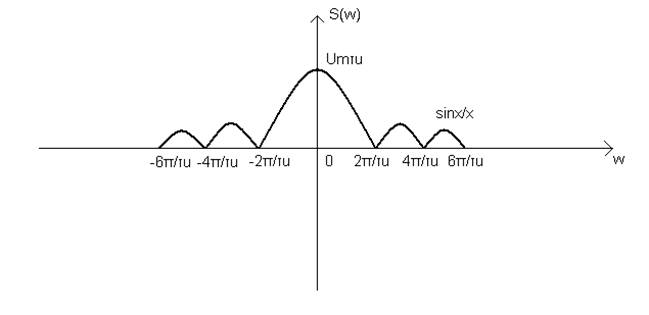
Рисунок 2

3.

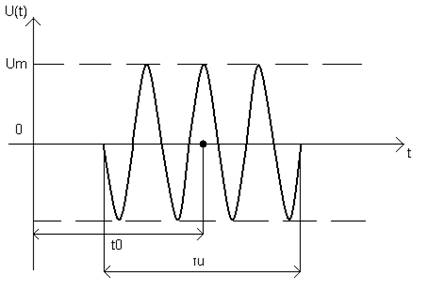
Рисунок 3

 

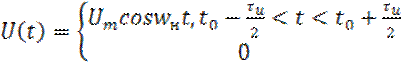
              (15)

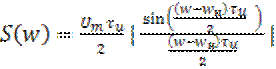                                                                               (16)

                                                                 (16)

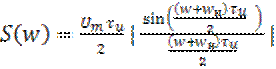                                                                               (17)

                                                                 (17)

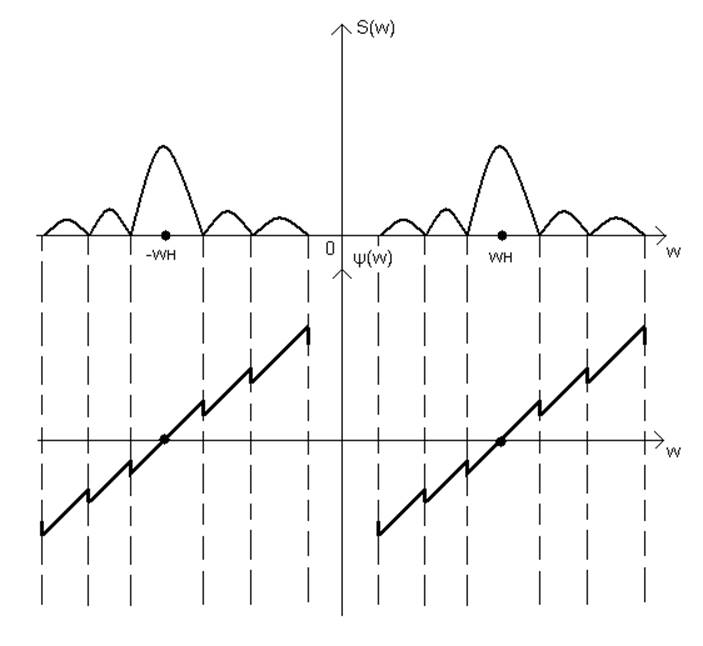
Рисунок 4

Спектры прямоугольных радиоимпульсов отличаются от спектров видеоимпульсов лишь смещением по оси частот на  и уменьшением в 2 раза модуля спектральной плотности.

4.

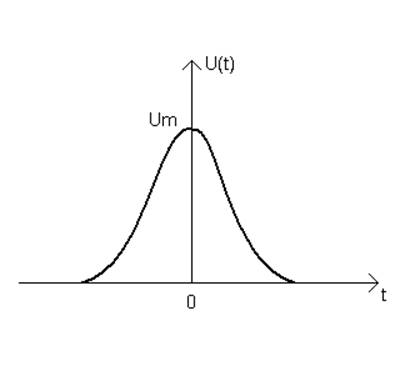
Рисунок 5

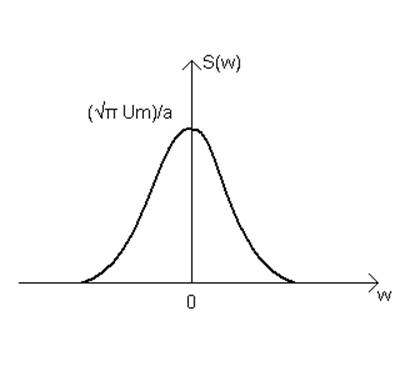
Рисунок 6

                                                                                                 (18)