Спектры непериодических сигналов. Спектральное представление непериодических сигналов. Спектр прямоугольного видеоимпульса, страница 2

a – постоянная, определяющая длительность импульса.

Спектральная плотность:

                                                                            (19)

В виду четности (18) спектр ее вещественный, причем он также колоколообразный (6).

Данный сигнал очень удобен в теории сигналов:

1) Он и его спектр выражаются одинаковыми функциями, для получения одной функции из другой нужно заменить t на w.

2) Для Гауссового импульса:

 

5.

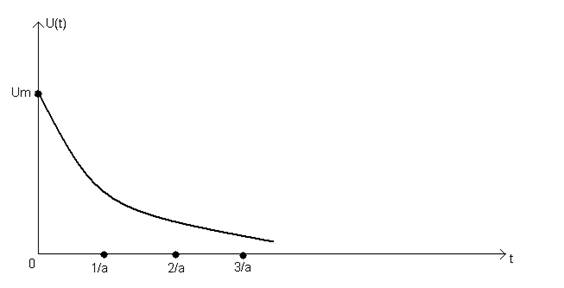
Рисунок 7

                                                                                       (20)

                                                                                                        (21)

                                                                      (22)

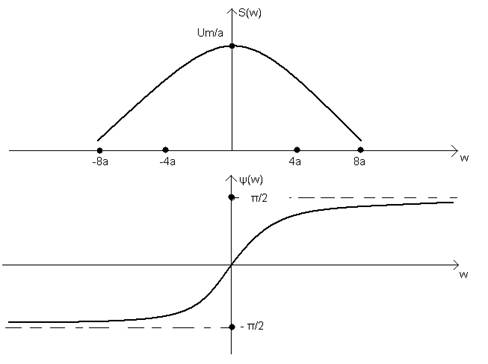
Рисунок 8

Некоторые спектры одиночных сигналов:

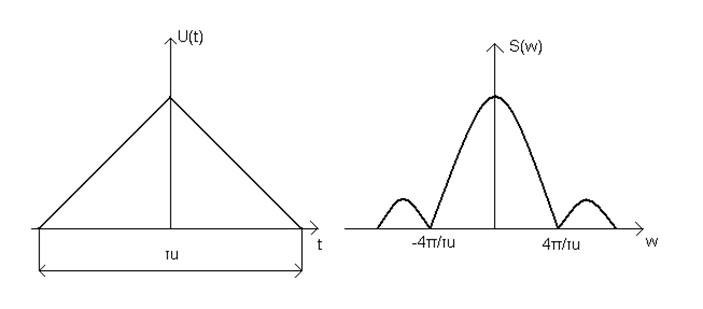
Рисунок 9

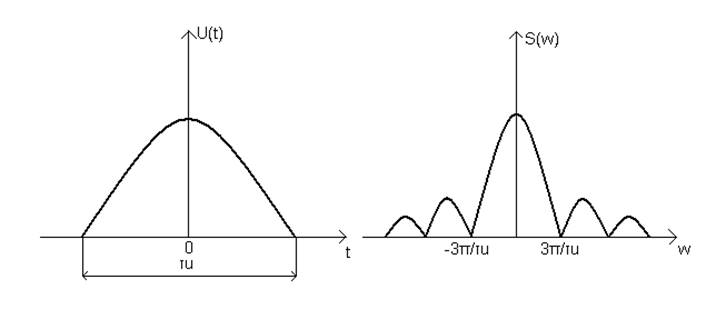
Рисунок 10

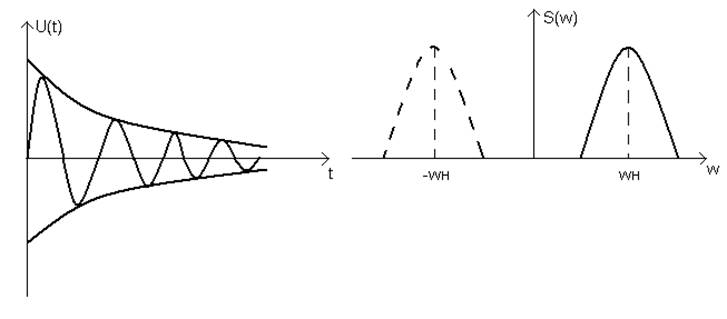
Рисунок 11

6. Для изученных δ-функций и ФВ преобразование Фурье в математическом смысле нету. Но в технических приложениях ППФ распространяют и на эти обобщенные функции.

                                                  (23)

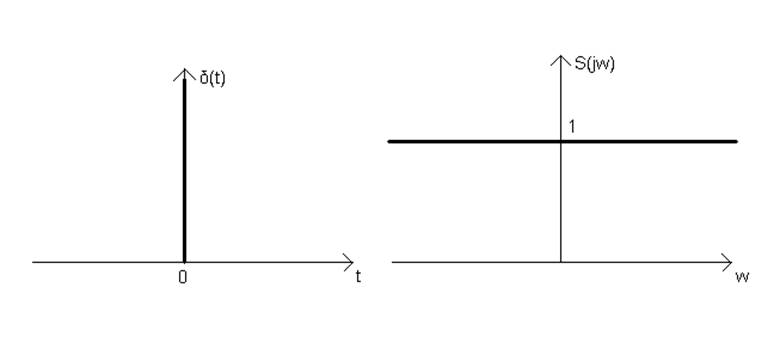
Рисунок 12

Из частотно-временной дуальности преобразования Фурье следует, что если спектром δ-функции является S(jw)=S(w)=1, то спектром функции S(t)=1 будет δ-функция δ(jw)=2πδ(w) – рисунок 12.

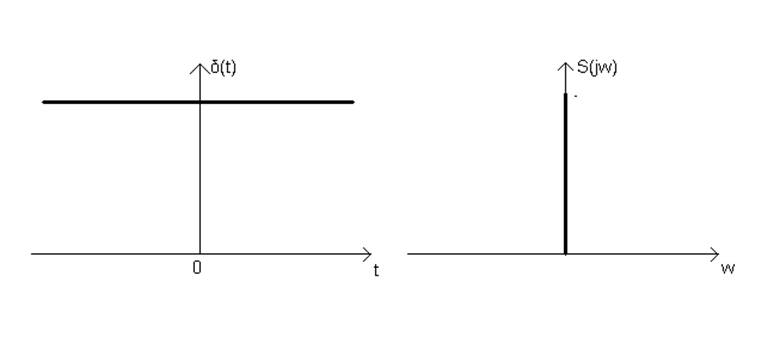
Рисунок 13

Спектральными функциями гармонического сигнала являются δ-функции.

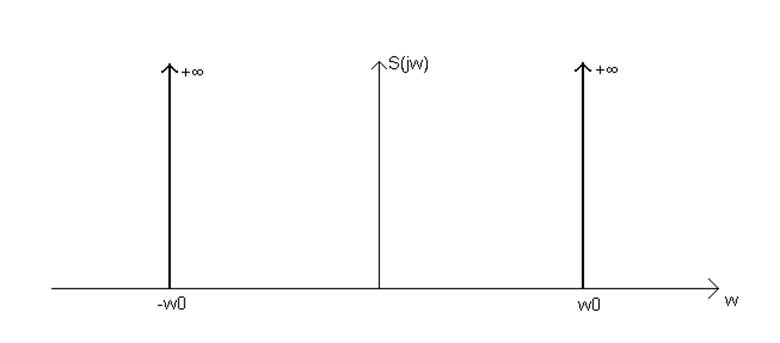
Рисунок 14

Спектральная плотность ФВ 1(t):

                                                                                          (24)

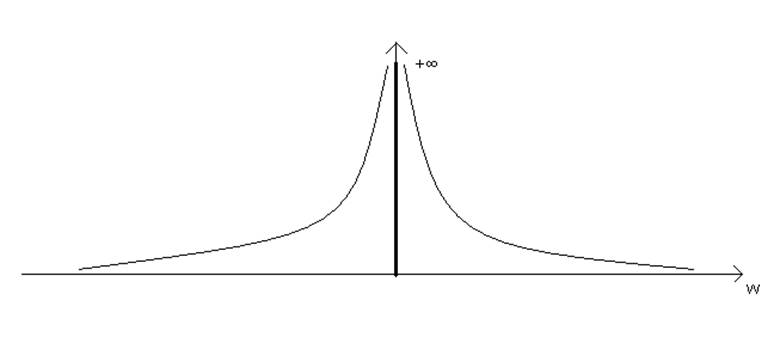
Рисунок 15

В (24) первое слагаемое – спектральная плотность переменной составляющей функции 1(t) (мгновенный перепад обладает неограниченно широким спектром – рисунок 15). Второе слагаемое – спектральная плотность постоянной составляющей функции 1(t).

8. Рассчитаем энергию непериодического сигнала, выделяемая на сопротивлении R=1 Ом.

 

 

                                           (25)

Изменив порядок интегрирования в правой части запишем:

                                             (26)

                                                                     (27)

(27) – теорема Релея, позволяет определить энергию сигнала через его спектральную плотность.

В (27) квадрат модуля спектральной плотности характеризует распределение энергии в спектре сигнала f(t).

 – энергетический спектр сигнала.

Эффективная ширина спектра – диапазон частот, в котором определена основная часть энергии сигнала.

Например, в случае одиночного прямоугольного видеоимпульса 90% энергии сигнала сосредоточено в первой арке (0; 2π/τ_u).

 – скалярное произведение сигналов, пропорциональных взаимной энергии                                                                (1)

U(t)=V(t), поэтому скалярное произведение переходит в энергию сигнала.

                                                                                  (2)

Пусть сигналы U(t) и V(t) заданы своими спектральными плотностями:

                                                                                (3)

                                                                                (3)

Из (3) в (1):

 

 

 – обобщенная формула Релея: скалярное произведение двух сигналов пропорциональное спектральному произведению их плотностей                                                                              (4)

Из (4) вытекает:

                                                                        (5)

 

                                                                                  (6)

В (6)  – взаимный энергетический спектр сигналов.

(6) показывает тонкую структуру связи двух сигналов: максимальная взаимная энергия сигналов будет на тех частотах, где спектры сигналов перекрываются.

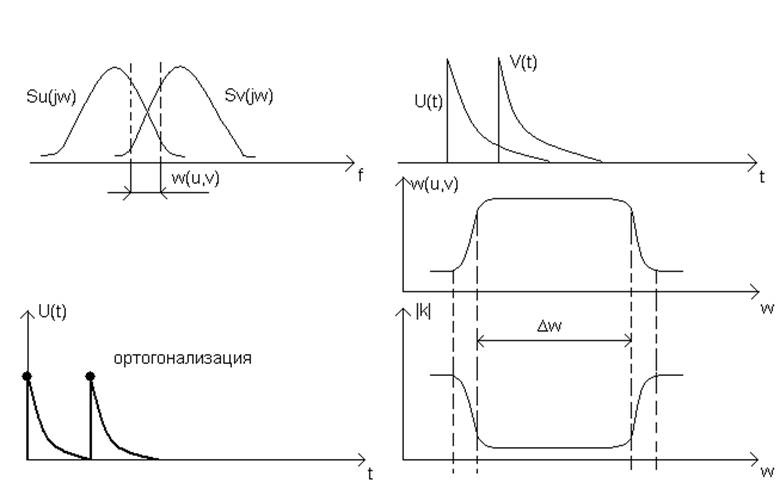
Рисунок 16

Если в (6) U=V, то тогда  есть произведение , а это равно .

 - спектральная плотность энергии сигнала (энергетический спектр)                                                                                       (7)

                                                                (8)

Из (8) следует, что энергия любого сигнала может быть представлена, как результат формирования вкладов от разных интервалов частотной оси.

Энергетический подход к изучению и анализу сигналов связан с потерей информации в спектре ФЧС, так как энергетический спектр в (7) не зависит от фазы. В частности при энергетическом подходе все сигналы одинаковые по форме, но различающиеся своим положением на оси времени есть идентичные.