Основы теории случайных сигналов. Случайные величины (СВ) и их характеристики. Спектральное представление стационарного случайного процесса (ССП). АКФ и ЭС ССП

Лекция 12-13

Основы теории случайных сигналов

1) Случайные величины (СВ) и их характеристики.

2) Случайные процессы (СП) и их характеристики.

3) Спектральное представление стационарного случайного процесса (ССП). АКФ и ЭС ССП.

1. Практически все сигналы могут быть представлены случайной моделью. Случайный сигнал характеризуются тем, что его мгновенные значения не могут быть заранее предсказаны и вычислены.

СВ анализируются в теории вероятности. Вероятностные законы возникают всегда, если физическая система порождающая сигнал, является системой более мелких подсистем, совершающие некоторое индивидуальные движения, в большей или меньшей степени независимая друг от друга.

В основе теории вероятности лежит понятие полного множества элементарных сходов (случайных событий):  - исходы некоторого случайного эксперимента. Каждому событию  ставится в соответствие  - вероятность.

Аксиомы теории вероятности:

1) .

2) .

Если A – некоторое сложное событие, то его вероятность равна сумме всех элементарных вероятностей:

Вероятность – абстрактная величина. Эмпирически она оценивается частотой благоприятных исходов. Если проведено N независимых испытаний, причем n раз наблюдалось событие A, то выборочная оценка вероятности P(A) будет равняться:

                                                                                                               (1)

Функция распределения (ФР) и плотность вероятности (ПВ).

Пусть X – случайная величина (СВ), то есть всевозможные вещественные числа x, принимающие случайные значения на (-;+). Тогда ФР СВ X – это неслучайная функция F(x) вещественного аргумента x.

Если X принимает любые значения, то F(x) является гладкой неубывающей функцией, значения которой лежат в интервале . При этом F()=1, F(-)=0.

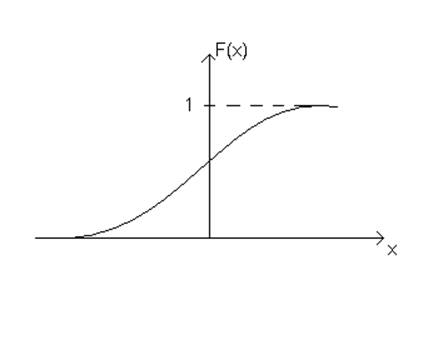
Производная от ФР – плотность распределения вероятности.

Очевидно, что p(x)dx – есть вероятность попадания СВ X в интервал (x;x+dx).

Для непрерывной СВ x p(x) представляет собой гладкую функцию. Если x – дискретная СВ, то есть принимающая конкретные значения {x₁,x₂,…,x_n} с вероятностями {P₁,P₂,…,P_n}, то:

.

Для плотности вероятности как дискретной, так и непрерывной СВ справедливы условия:

1)

2)  - свойство нормировки.

3)  - заданная функция от x (исхода случайного испытания), то ее среднее значение равно:

                                                                                       (2)

Из (2) следует, что наибольший вклад дают те значения x, при которых одновременно велики  и .

Числовые характеристики СВ:

1) Математическое ожидание (МО):

                                                                                         (3)

Оно обобщает в вероятностном смысле понятие среднего арифметического.

2) Средний квадрат СВ:

                                                                                                (4)

3) Дисперсия:

                                                            (5)

4) Средне квадратическое отклонение (СКО):

                                                                                                                (6)

Это количественная оценка разброса результатов отдельных случайных испытаний относительно выбранного среднего.

Равномерное распределение СВ:

Пусть некоторое СВ X может принимать значения из области , причем вероятности попадания в любые внутренние подинтервалы одинаковой ширины  равны. Тогда плотность вероятности:

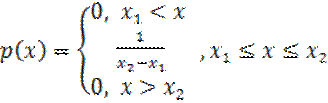
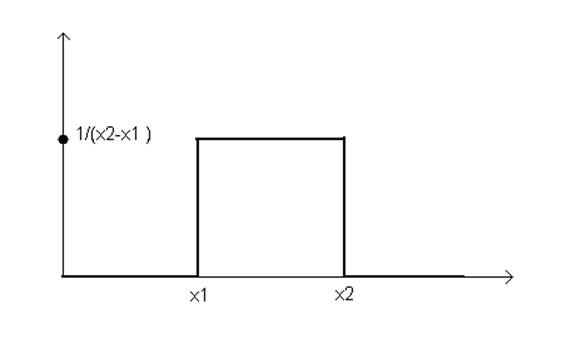
ФР: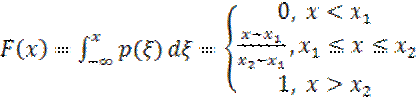  

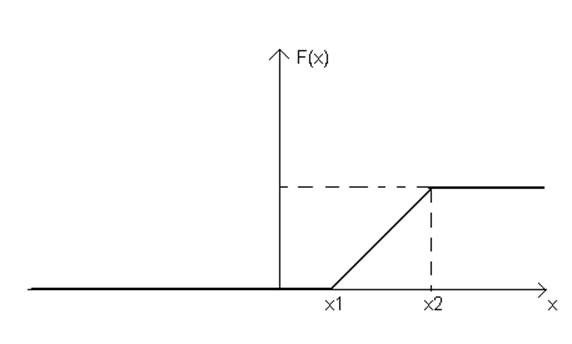
 - совпадает с центром интервала (;)

Равномерное распределение часто используется в теории погрешности.

Гауссово – нормальное распределение:

наиболее важный закон распределения:

 - плотность распределения                                                 (7)

Определяется двумя числовыми параметрами.

График представляет собой колоколообразную кривую с точкой максимума x=m.

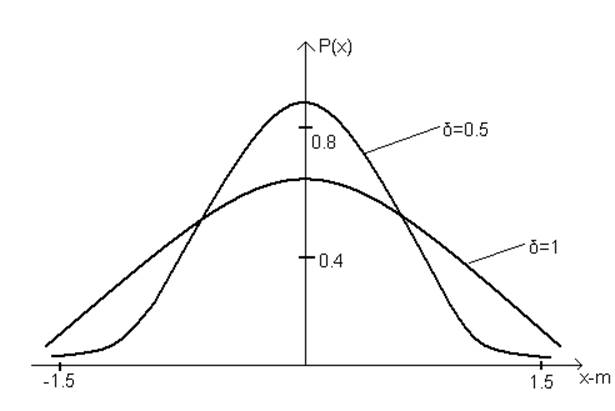
m определяет положение пика, а  - его величину и ширину колокола.

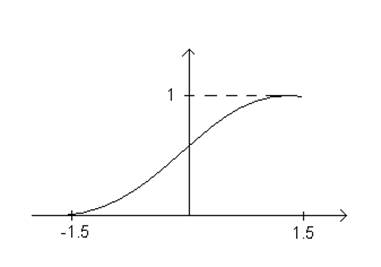
Функция распределения Гауссовой интегральной величины:

                                                                                   (8)

График имеет вид монотонной кривой и изменяется от 0 до 1.

2. Теория СВ изучает случайные явления, рассматривая их как некоторые зафиксированные результаты эксперимента.

Для описания сигналов являющихся СВ, изменяющимися во времени, методы классической теории вероятности недостаточны, подробнее изучает теория случайных процессов.