Основы теории случайных сигналов. Случайные величины (СВ) и их характеристики. Спектральное представление стационарного случайного процесса (ССП). АКФ и ЭС ССП, страница 3

                                                                                  (20)

Для того, чтобы описать весь ансамбль реализаций ССП x(t), надо допустить, что S(w) – случайная функция частоты. То есть СП во временной области связан с другим СП частотной области. Но какими свойствами должны обладать случайные функции S(w), чтобы процесс x(t) был стационарен и чтобы (20) была спектральным представлением S(w)?

Для ответа на поставленный вопрос, прежде всего, проведем усреднение мгновенных значений по ансамблю:

 

Это равенство справедливо для любых t, если среднее значение спектральной плотности .                                                                                           (21)

S(w) отдельных реализаций ССП должна иметь нулевые МО на всех частотах.

Далее, при каких условиях АКФ K(τ) будет зависеть лишь от сдвига τ между сечениями?

Сигнал x(t) – комплексный и на ряду с (20) справедлива (22):

                                                                  (22)

Запишем выражения АКФ, используя спектральные разложения случайного сигнала в (20) и (22):

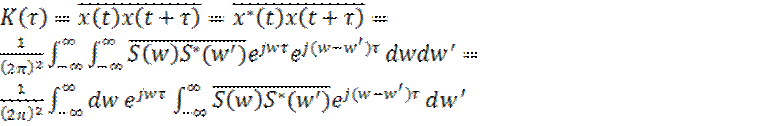                                               (23)

В (23) множитель  имеет смысл АКФ случайный спектральной плотности S(w).Для того, чтобы величина K() не зависима от t, надо по (23) выполнение следующей пропорциональности:

   (24)

S(w) ССП должна быть дельта кореллирована. Спектры, отвечающие двум несовпадающим частотам некореллированны между собой, и в тоже время дисперсия неограниченно велика.

Энергетический спектр ССП:

из (24) следует, что                                   (25)

W(w) – ЭС ССП x(t).

Подставив (25) в (23) получаем:

 - теорема Винера-Хинчина                                (26)

АКФ и ЭС ССП, имеющие нулевое МО связаны между собой преобразованием Фурье:

                                                                                (27)

Если в (26) , то , и:

                                                                                (28)

Дисперсия равна средней мощности ССП есть, следовательно, суммой вкладов от всех частот. Величина W(w) пропорциональна удельной средней мощности, соответствует единичному частотному интервалу в окрестностях выбранной частоты w. Энергетический спектр вещественный и неотрицательный.

                                                                                                             (29)

Он не несет никакой информации о фазовых соотношениях (соответствиях) отдельных спектральных компонент, поэтому, по ЭС невозможно восстановить какую-либо отдельно взятую реализацию.

Интервал корреляции:

АКФ ССП стремится к 0 с ростом временного сдвига τ. Чем быстрее убывает функция K(τ),тем меньшей оказывается статистическая связь между мгновенными значениями случайного сигнала в два несовпадающие моменты времени.

Числовой характеристикой для оценки скорости изменения реализации СП есть интервал корреляции.

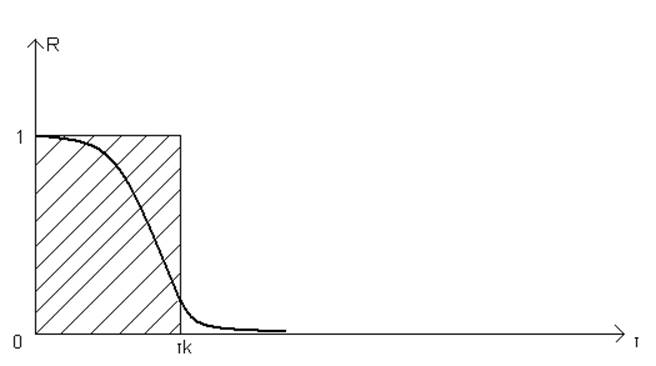
Из рисунка следует:

                                                                                 (30)

Возможен вероятностный прогноз поведения любой реализации случайного сигнала на время , если известна информация о поведении в прошлом. Но нельзя прогнозировать на время больше  корреляции (мгновенные значения, столь далеки во времени, практически не коррелированны).

 

Эффективная ширина спектра (ЭШС):

пусть случайный сигнал характеризуется F(w) – односторонним ЭС, причем Fmax(w) – максимальное значение этой функции.

 

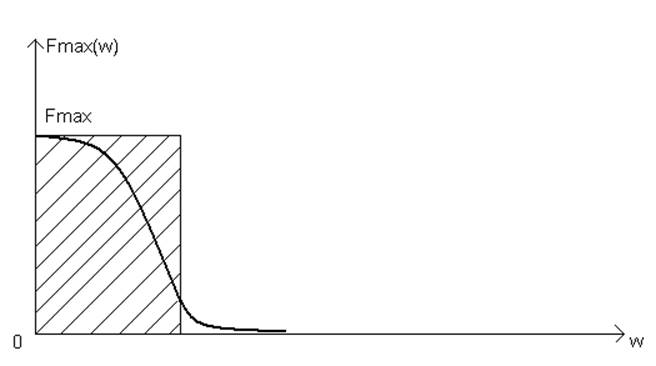
                                                                                     (31)

Дисперсия шума: .

Между  и  существует соотношение неопределенности:

 

Чем шире ЭС шума, тем хаотичнее изменяется во времени его реализация.

Белый шум (БШ):                                  

БШ – это ССП, у которого ЭС на всех частотах:

 

По теореме Хинчина:

                                                                       (32)

Из (32) следует, что средняя мощность БШ бесконечно большая.

БШ является дельта - коррелированным СП, то есть скорость изменения мгновенных значений реализации БШ неограниченно большая.

БШ – это абстрактная математическая  модель, но достаточно широкополосные СП могут быть представлены БШ - моделью, если полоса пропускания цепи, на которую воздействует СП, оказывается существенно уже ЭШС шума.