Основы теории случайных сигналов. Случайные величины (СВ) и их характеристики. Спектральное представление стационарного случайного процесса (ССП). АКФ и ЭС ССП, страница 2

СП X(t) – функция характеризуется тем, что в любой момент времени t, принимаемые ею значения являются СВ. Если мы изменим на определенном промежутке времени мгновенное значение случайного сигнала, то получим лишь единственную реализацию СП.

СП выраженные через совокупность таких реализаций – статистический ансамбль. Например, таким ансамблем служит: {x₁(t),x₂(t),…,x_n(t)}, которые можно наблюдать на выходах одинаковых генераторов шума.

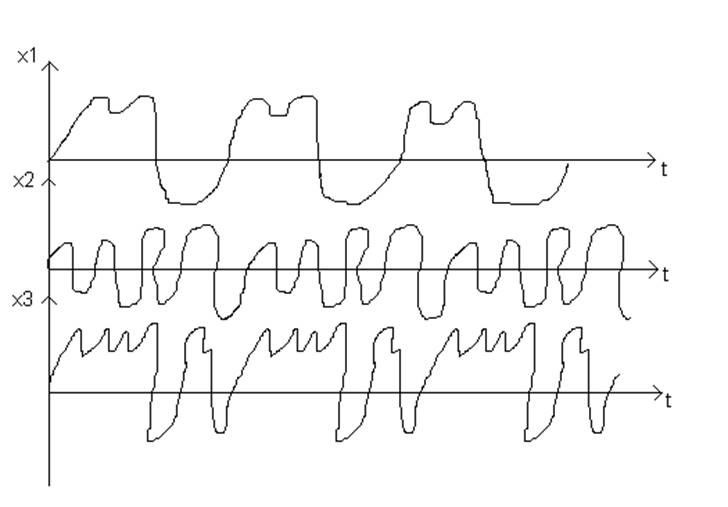
ПВ случайного процесса:

пусть X(t) – СП, заданный ансамблем реализаций:

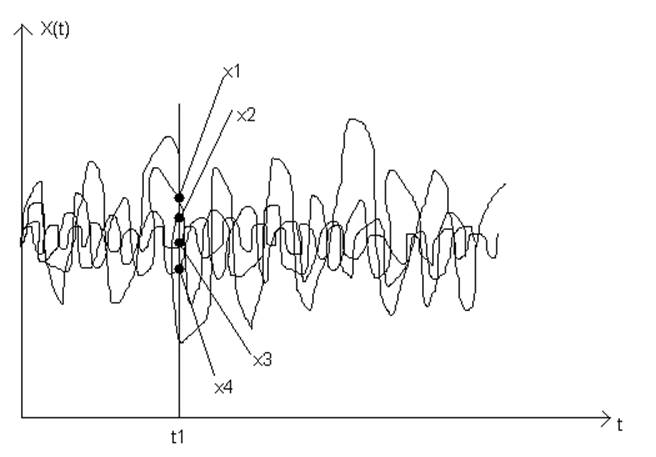
t1 – некоторый произвольный момент времени.

Фиксируя величины {x₁(t),x₂(t),…}, получаемые в отдельных реализациях, мы получаем одномерное сечение данного СП, и наблюдаем СВ X(t).

Ее плотность вероятности: P(x,t₁) называется одномерной ПВ случайного процесса X(t) в момент времени t₁. Впрочем, одномерная ПВ недостаточна, что бы судить о характере развития реализации.

Если взять два сечения t₁ и t₂ (t₁t₂), то возникшая при этом СВ представляется двумерной ПВ P(x₁,x₂,t₁,t₂), она более полно опишет процесс.

Естественным обобщением является n-мерное значение (n>2), приводящее к n-мерной ПВ: P(x₁,x₂,…,x_n,t₁,t₂,…,t_n).

Однако, получение этих плотностей математически трудно.

Числовые характеристики СП:

на практике значительно удобнее оперировать с моментными функциями СП.

                                                                         (9)

1) Математическое ожидание – среднее значение X(t) в текущий момент времени t.

Усреднение проводится по всему ансамблю усреднения процесса.

2) Дисперсия:

                    (10)

Это позволяет судить о степени разброса мгновенных значений СП, принимаемых отдельными реализациями фиксированными значениями.

3) АКФ – двумерный центральный момент.

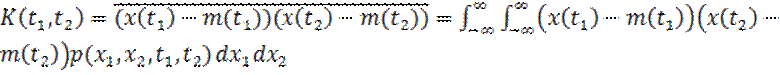                                                                             (11)

АКФ характеризует степень связи тех СВ, которые наблюдаются в моментах времени .

Сравнивая (10) и (11) можно увидеть, что при  АКФ численно равна дисперсии:

                                                                                                  (12)

Так принято называть СП, статистические характеристики которых неизменны во времени.

Говорят, что СП стационарен в узком смысле, если любая его n-мерная ПВ инвариантна относительно временного сдвига τ.

P(x₁,x₂,…,x_n,t₁,t₂,…,t_n)= P(x₁,x₂,…,x_n,t₁+ τ,t₂+ τ,…,t_n+ τ)                                   (13)

Говорят, что СП стационарен в широком смысле, если m и Dx постоянны, а АКФ определяется разностью:

 

Из стационарности в узком смысле следует стационарность в широком смысле, но не наоборот.

Для ССП АКФ имеет следующие свойства:

1) Четность: .

2) Абсолютное значение для любых : .                         (14)

Часто удобно вводить нормированную АКФ:                   (15)

Также часто называемую коэффициентом корреляции ССП.

Из (15) следует: R(0)=1.

Свойство эргодичности: ССП называется эргодическим, если при нахождении любых стохастических характеристик усреднение по статистическому ансамблю может быть заменено усреднением во времени.

Операция усреднения выполняется над единственной реализацией X(t), протяженность которой .

Математическое ожидание эргодического ССП:

                                                                   (16)

Математическое ожидание равняется постоянной составляющей выбранной реализации.

Dx эргодического ССП (17):

 

Поскольку  есть средняя мощность реализации, а  - мощность постоянной составляющей, то дисперсия равна мощности флюктуационной составляющей эргодического ССП.

АКФ эргодического процесса:

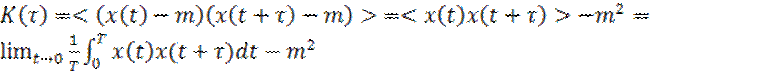                                                                        (18)

Для того что бы СП был эргодическим, он должен быть стационарен в широком смысле.

Достаточным условием эргодичности является стремление к 0 АКФ при неограниченном росте временного сдвига τ.

                                                                                                  (19)

Между корелляционными и спектральными свойствами случайных сигналов существует глубокая и тесная связь.

Пусть имеем X(t) – стационарный случайный процесс, обладающий нулевым МО. Отдельная взятая реализация ССП есть детерминированная функция, которую можно представить ОПФ: