Исследование характеристик типовых звеньев систем автоматического регулирования. Линейное динамическое звено, страница 3

   Параметры k и Т инерционного звена могут быть определены также по переходной характеристике, полученной экспериментально. Из рис. 3 видно, что переходная характеристика есть возрастающая экспонента. Постоянная времени Т определяется геометрически как величина проекции касательной в начале экспоненты. Коэффициент усиления k находится по ординате переходной характеристики при  t              ¥

Постоянная времени Т характеризует степень инерционности звена, т.е. длительность переходного процесса, которая принимается равной 3 Т.

1.3. Интегрирующее     звено.

Уравнение звена

dy

= kx,                                                                                                (39)

dt или в интегральной форме    

                                                                                                                     (20)                                                                                                                                                                                                                                                                                                                       

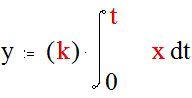т.е. выходная величина пропорциональна интегралу от входной величины по времени .

Передаточная  функция  И  ККУ звена

К(р) =  k/p;          K(jw) =  k/(jw).                                                       (21)

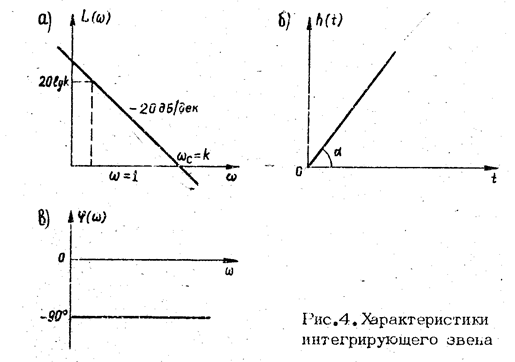
ЛАХ интегрирующего звена

L(w)  = 20 lg k – 20 lg w                                                             (22)

имеет вид прямой с наклоном - 20 дБ/дек.

ЛФХ эвена ф(w) = -90⁰ .                                                                               (23)

Переходная фикция

h(t) = kt .                                                                                    (24)

Частотные и переходная характеристики интегрирующего звена приведены на рис, 4. График L(w)  пересекает ось абсцисс при частоте среза w_c = k.Переходная характеристика есть прямая линия с наклоном к = arctgk.

1.4. Дифференцирующее   звено.

Идеальное дифференцирующее звено дает на выходе величину, пропорциональную производной от входной величины . Уравнение его

              dx

   y = k          .                                                                                                 (25)

dt

Передаточная функция и ККУ звена

К(р)=kp;K(jw)=jwk.                                                                   (26)                                                                    

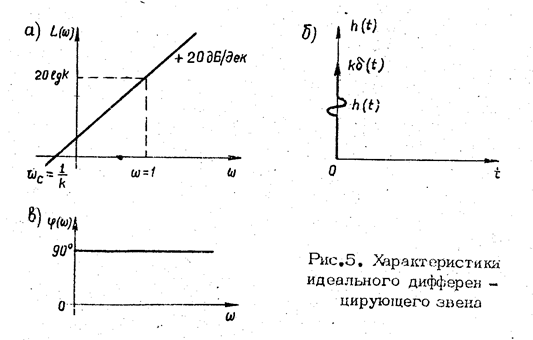
ЛАХ дифференцирующего звена

L(w) = 20 lg k + 20 lg w                                                                       (27)

имеет вид прямой с наклоном +20 дБ/дек. Частота среза

w_c =  1/k.

ЛФХ звена ф(w) = 90⁰ .                                                                                (28)

Переходная функция

h(t)=kd(t),                                                                                   (29)                            

где  d(t) - дельта-функция.

График переходной функции имеет вид мгновенного импульса с амплитудой, равной бесконечности.                   

На рис. 5 приведены частотные и переходная характеристики идеального дифференцирующего звена.

Идеальное дифференцирующее звено практически не может быть реализовано. Реальные дифференцирующие звенья всегда имеют малые параметры, создающие инерционность. Реальное дифференцирующее звено описывается уравнением

dy                   dx       

   T          +  y =  k        .                                                                (30)

dt                    dt 

Передаточная функция и ККУ звена  

kp                              jwk 

   K(p) =                ;     K(jw) =                  .                                  (31)