Исследование характеристик типовых звеньев систем автоматического регулирования. Линейное динамическое звено

Лабораторная        работа     №   12

ИССЛЕДОВАНИЕ  ХАРАКТЕРИСТИК ТИПОВЫХ ЗВЕНЬЕВ

СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ                                                

Цель   работы. Ознакомиться с экспериментальными  способами      определения частотных и переходных характеристик типовых  звеньев систем автоматического   регулирования.

1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

Линейное динамическое звено - это любой элемент системы автоматического регулирования (CAP), связь между выходной Y и входной X величинами которого определяется линейным дифференциальным уравнением

a_ny⁽ⁿ⁾ + a_n-1y^(n-1) + … + a₁y¹  + a₀y  =  b_mx^(m) + b_mx^(m-1)  + … +

+ b₁x¹+ b₀x                                                                         (1)

где  n - порядок уравнения (n =>m).    Типовыми называют динамические звенья, работа которых    описывается дифференциальным уравнением не выше второго порядка.

По дифференциальному уравнению звена можно определить его передаточную функцию

b_mp^m + b_m-1p^m-1 + … + b₁p + b₀          Y(p)

K(p) =                                                                  =                                          (2)

a_npⁿ  +  a_n-1p^n-1 +  …  + a₁p + a₀         X(p)

и комплексный коэффициент усиления (ККУ)

b_m(jw)^m + b_m-1(jw)^m-1 + … + b₁(jw) + b₀     Y’                  

K(jw) =                                                                          =                                 (3)

a_n(jw)ⁿ + a_n-1(jw)^n-1 +  …  + a₁(jw)  +  a₀    X’

где Х(р), Y(p) - изображение по Лапласу входной и выходной  величины;   Х’ = Х(m), Y’ =Y_me ^jф  - комплексные амплитуды гармонических колебаний на выходе и входе звена.

ККУ имеет определенный физический смысл. Если на вход линейного звена подать синусоидальное колебание с амплитудой Х_m, и частотой w

х(t)=X_msin(wt),                                                                                            (4) то в установившемся режиме на выходе звена будут  синусоидальные колебания с той же частотой w, но с амплитудой Y_m   и сдвигом по фазе ф

y(t) = Y_msin(wt+ф),                                                                     (5)

При этом модуль  ККУ

Y_m

Mod K(jw) = K(w) =                                                                      (6)

X_m

показывает, во сколько раз изменилась амплитуда колебаний,  а аргумент  ККУ

arg K(jw) = ф(w) = ф                                                                     (7)

показывает сдвиг фазы колебаний на выходе по отношению к колебаниям на входе звена.

Для описания динамических свойств звеньев CAP применяются два вида характеристик - частотные и переходные.

Частотные характеристики представляют в различных, видах зависимости KKУ от частоты w. Наиболее   широко используется амплитудная частотная характеристика К(w)- зависимость модуля  ККУ от частоты  и фазовая частотная характеристика ф(w) - зависимость аргумента  ККУ от частоты.

Для инженерных расчетов более удобно амплитудную и фазовую частотные характеристики изображать в логарифмическом масштабе.

При построении логарифмической амплитудной частотной характеристики (ЛАХ) по оси ординат откладывают величину

L(w) = 20 lg K(w),                                                                         (8)

единицей измерения для которой является децибелл (дБ). По

                                                                                    1

 оси абсцисс откладывается круговая частота w             в

c

логарифмическом масштабе, т.е. фактически откладывается величина lg w, но указывается значение самой частоты w (рис. 1, а).

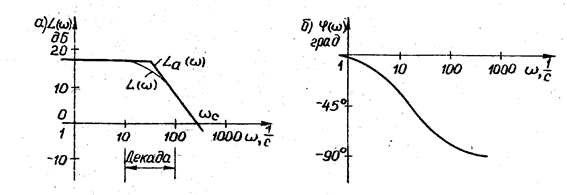
Рис. 1. Логарифмические частотные характеристики

Равномерной единицей на оси абсцисс является декада — любой отрезок, на котором значение частоты увеличивается в 10 раз. Точка пересечения ЛАХ с осью абсцисс называется частотой среза w_c . Начало координат обычно помещают в точке w = 1, так как  lg 1 = О. Точка же w = О лежит в -оо. Однако в зависимости от интересующего диапазона частот можно начало координат брать и в другой точке (w = 0,1; w = 10 или др.).

Преимущество ЛАХ перед обычными амплитудными частотными характеристиками заключается в том, что в большинстве практических случаев они могут быть представлены в виде ломаных линий - асимптотических ЛАХ  L_a(w). В связи с этим упрощаются расчеты и графические построения частотных характеристик.                         

При построении логарифмической фазовой частотной характеристики (ЛФХ) отсчет углов ф идет по оси ординат в обычном масштабе в угловых градусах. По оси абсцисс откладывается по-прежнему частота w в логарифмическом масштабе (рис.1,б).